부경대학교 전자정보통신공학부 AI응용시스템의 Linear Regression, Superviesed Learning, Regression and Classification 문제와 동일하다고 판단된다.
Polynomial Curve Fitting에 따른 Overfitting, Just-fit, Underfitting의 사례를 공부하였고 Hyperparameter값에 따라 Validaiton Data 및 Regulation에 대해 알아보았다. 또한 S-Fold Cross Validation에 대해 공부하였다.
Supervised Learning
먼저 Supervised Learning의 경우 인공지능 모델에게 정답과 학습문제를 알려주는 방식으로 학습하는 것이다. 어릴때 도형의 이해를 공부하여 보면서 외우는 것과 동일하다.
이러한 문제는 크게 Binary Classification, Multi-class Classificaion, Regression으로 구분되는데, Regression과 Classification의 경우는 출력이 연속변수이면 Regression, 이산 변수이면 Classification이라고 할 수 있으며 Label여부에 따라 지도와 비지도학습이 구분된다.
Supervised learning의 Learning Pipeline은 다음과 같이 나타낼 수 있다.
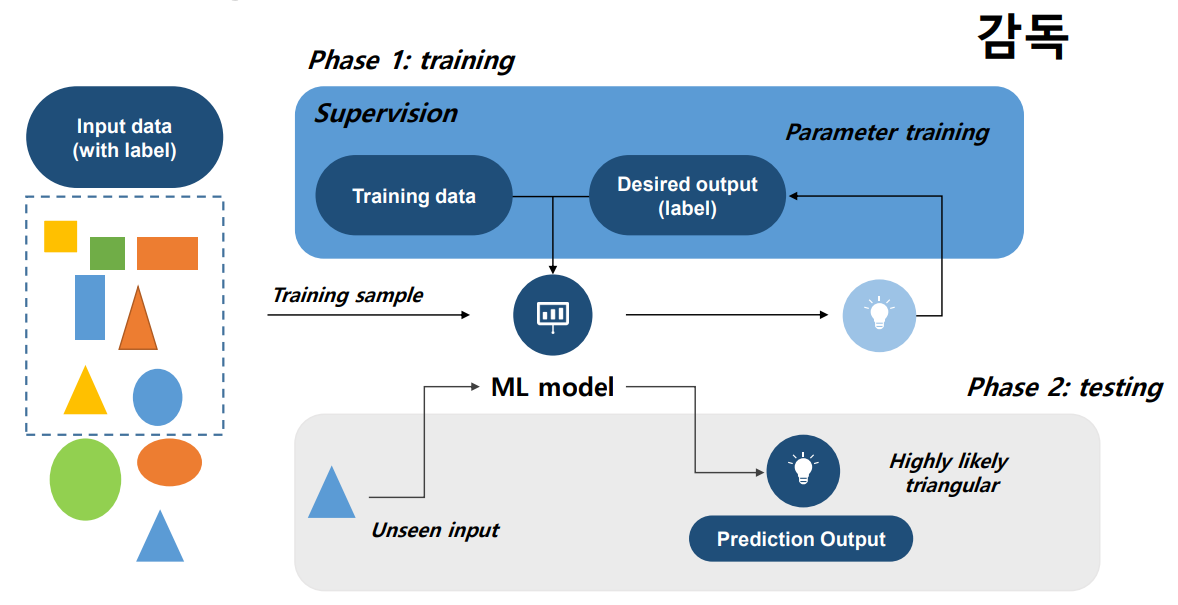
Supervised Learning의 학습 진행과정에서는 모델의 출력값과 정답과의 차이를 나타내는 Error Function이라는 것이 있다. 이를 최소화한게 MSE(Mean Square Error)이고 MSE값을 최소화하는 것이 알고리즘의 근본 사유라고 할 수 있다.
모델 학습 중요요소
모델의 학습에 있어 중요한 요소는 약 3가지다.
Feature Selection : 문제의 적절한 Feature를 선정하여 학습한다.
Model Selection : 주어진 문제에 가장 적합한 모델을 선택하여 문제를 해결한다.
Optimization : 모델 파라미터를 최적화하여 성능을 최대화한다.
또한, 현실 세계에 있는 모든 데이터에 대한 모델을 구성하기는 불가능에 가깝기 때문에 데이터의 결핍으로 인한 불확실성을 포함하게 되며 이로 인해 Generalization도 중요하다.
모델의 Generalization는, 모르는 데이터에도 우수한 성능을 제공해야 하는 것이 목표이며, Generalization Error의 최소화가 목적이다.
하지만 학습과정에서 직접적으로 Generalization Error를 낮출수 없기 때문에 Training Error, Validation Error, Test Set Error를 이용해 최소화하려 한다.
Error의 경우 e(h(x), y)로 계산하며 대표적으로 Squared Error와 Binary Error가 있다.
squared error : e(h(x), y) = (h(x) - y)^2
binary error : e(h(x), y) = 1(h(x) != y)
overall error : E((h(x) - y)^2]
이들은 손실함수, cost function, loss function이라고 불린다.
주요 error들은 다음과 같다.
error_training : 주어진 데이터셋에 맞추어 학습하는 데 사용하는 에러로 모델 파라미터 최적화에 사용
error_test : 현실 세계에 적용했을 때 나타나는 Generalization Error를 표현
모델의 학습에서 에러를 조절하고자 하는 목적은 2개가 있다.: error_test와 error_training가 가까워지도록, error_training의 값이 0에 가까워지도록.
1번 과정의 실패에는 모델의 분산이 커져, 학습데이터셋에 의존하는 overfitting 문제가 대두될 수 있으며, 정규화나 더 많은 데이터 셋으로 해결할 수 있다.
2번 과정의 실패에는 모델의 bias가 커져, underfitting 문제가 대두될 수 있으며, 최적화나 더 복잡한 모델을 사용해 해결할 수 있다.
variance와 bias 사이에는 서로 반비례 관계인 trade-off 관계가 나타난다.
Total Loss = Bias + Varinace (+ noise)
Underfitting, Just Fit, Overffitting
모델이 복잡한 경우 -> overfitting -> 분산 증가 -> bias 감소
모델이 단순한 경우 -> underfitting -> bias 증가 -> 분산 감소
하지만, 최근에는 복잡도의 증가속도가 데이터셋의 샘플 수 확보 속도보다 빨라 overfitting이 증가하는 추세다.
이를 Curse of Dimension 문제라고 부르며, 이를 해결하기 위한 가장 단순한 방법은 데이터셋을 늘리는 것이다.
데이터를 확보할 수 없는데 늘리기 위해서, Data augmentation이 등장했고,
주요 개념으로 Regularization, Ensemble이 있다. 두 개념은 추후 다시 다룬다.
Cross-Validaion
k-fold cross-validation : 학습 데이터셋을 k개의 그룹으로 나누어 (k-1)개의 그룹은 학습에 사용하고 1개의 그룹은 검증에 사용하는 방법으로, 부족한 데이터셋의 빈틈을 채워줄 수 있는 방법이다.
