선형 모델들은 다양한 장점들을 가진다. 초심자들에게 가장 쉬운 단순화된 알고리즘이고 쉽게 접하기도, 해석하기도 쉽다는 장점이 있고 테스트 데이터와 학습 데이터에 대해 일반화가 더 쉽다는 것 역시 상당한 장점이라고 할 수 있다.
선형 모델에 대해 임의의 가설 세트 H를 만들 때, 해당 직선 H는 다음과 같은 식을 만족한다. 이때 어떠한 인풋에 대해 phi의 임의 추출기를 사용하여 해당 모델에 대한 phi(x)로 만들어 내며 해당 식은 아래와 같이 Transposed theta vector와 phi(x) vector의 inner product 값으로 나타낼 수 있다.


Linear regression Framework은 다음과 같이 정의할 수 있다.
먼저 Example에 대해 Training Data를 찾고, Univariate linear model에 대해 Predictor 값을 구한다. 그 후, 앞서 소개했던 MSE값을 이용하여 해당 Predictor가 좋은지를 판단한다. 이후, Gradient Descent algorithm으로 이를 계산할 수 있는 방법에 대해 조사한다.
MSE를 최소화하는 데에 도움이 되는 L2 cost Function에 대해 기술하면 다음과 같이 표현이 가능하다.
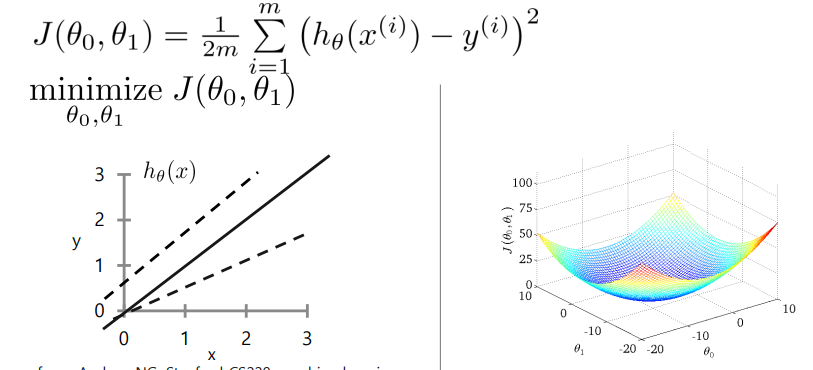
이때 Weight와 Bias를 구할 때에는 Optimization을 사용하는데, D차원의 위치에서의 정의를 이용하면 아래와 같다.
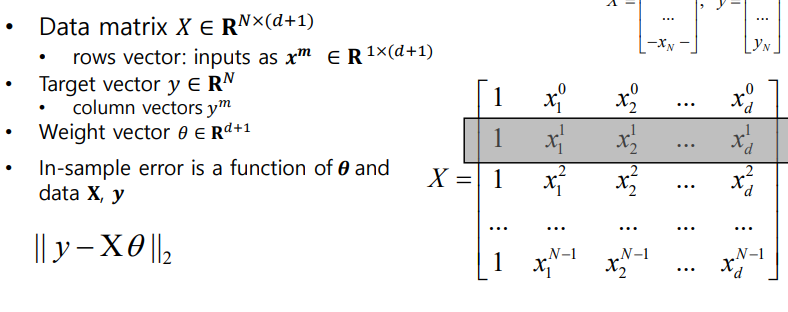
이때 최소화된 Error Function을 사용하여 선형 회귀의 Solution을 구하면
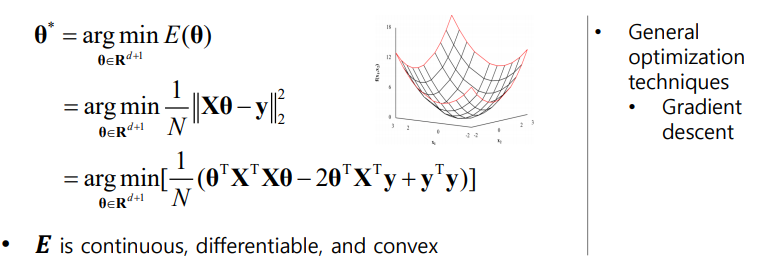
와 같다. 이때 최소화할 수 있는 조건을 찾아내기 위한 theta를 찾기 위해 arg min 식을 사용하였다.
theta를 찾기 위해 theta에 대한 Delta와 E의 내적값을 이용하면 아래와 같이 나타낼 수 있다.

대수적으로 이를 풀이하기 위해 Gradient Descent Algorithm을 사용하면, 아래와 같이 식을 구할 수 있고, 수렴할 때까지 이를 반복하면 아래와 같이 식으로 나타낼 수 있다.

물론, Gradient Descent도 완전한 것은 아니기에 Stochastic Gradient Descent나 Mini-batch Stochastic Gradient Descent를 통해 이를 개선할 수 있고, 완전이차함수가 아닌 경우도 충분히 있게 되므로 Local Minima(극소점) 또는 Saddle points(평탄화지점)에 대해 개선한 AdaGrad, RMSProp, Adam를 이용하여 이를 보완할 수 있다. 이허한 점 뿐만 아니라 데이터 셋이 너무 클 경우 Transposed Matrix 및 이들간의 내적 및 인버스 값에 대해 계산이 너무 크다는 점도 한몫한다.
아래는 내가 과제하면서 만든 기초 이론들이다.
1. Basis Function Model
Basis Function Model이란 매개변수 w에 대해서는 선형성을 유지하지만 x에 대해서는 비선형성을 가지게 되어 Under-fitting을 방지하게끔 하는 방법이다. 이러한 특징을 이용하여 매개변수 w를 구하는 방법들에는 Maximum Likelihood (ML), Least Square Solution (LSS), Gradient Descent (GD), Stochastic Gradient Descent(SGD), Mini-batch Stochastic Gradient Descent(MSGD)가 있다.
-
Least Square Solution
-최소제곱해로 불리는 Least Square Solution 방식은 실제 값과 가설에 의한 예측 값의 차이가 가장 작은 계수를 계산하여 w를 구하는 방법으로,
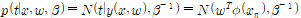
이 됨을 확인할 수 있다. 이러한 최소제곱해는 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법이지만 Solution이 특징 변수와 샘플 건수에 비례하므로 계산 비용이 높다는 점과 과도하게 튄 노이즈(Outline)에 취약하다는 점이 한계로 꼽힌다.
-
Gradient Descent
어떤 Linear Regression Model의 손실 함수인, 아래 조건을 통해 그려지는 MSE가 있을 때,
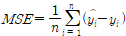
(단,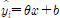
)
를 계수, x를 실제값, b를 절편으로 가지게 되므로 학습을 통해 알아보고자 하는 미지수 모델 parameter 는 1개의 최적해를 갖는 이차함수 형태이며, weight a를 최소 점으로 가지게 된다.
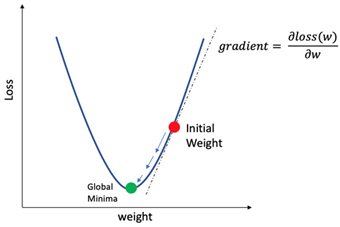
그림 2. a를 Weight로 가지는 Loss Function
일반적인 정규방정식 형태나 최소 제곱법은 이러한 a를 한 번에 찾고자 할 때 이용이 가능하고, Gradient Descent로 대표되는 경사하강법은 손실 함수에 대해 임의의 한 위치에서 기울기를 계산하여 기울기가 0이 되는 방향으로 유도하여 최적해 a를 찾는 방법이다.
이렇게 a를 찾기 위해 Sequential update를 이용하며 그로 인해 Loss Graph의 Global loss minimum은 아래와 같이 나타낼 수 있다.
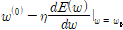
(단, mu는 Learning Rate)
이러한 Gradient Descent의 경우, 일정 평평한 지역으로 들어가게 될 시에는 집계가 불가능하거나(Plateau Problem), 실제 손실 함수의 형태는 위 그래프처럼 깔끔하지 않으므로 최소값, 최대값이 아닌 극소값, 극대값을 찾을 수 있다는 것(Nonconvex Error Function)이 문제가 될 수 있다.
또, 학습률이 매우 작을 경우 수렴되는 속도가 너무 느려질 수 있으며, 너무 크게 될 경우에도 Overshooting 또는 집계가 불가능할 수 있다. -
Stochastic Gradient Descent,
확률적 경사하강법(Stochastic gradient descent, SGD)은 배치 크기가 1인 경사하강법 알고리즘으로, 데이터 세트에서 임의의 균일 선택한 하나의 예를 의존하여 각 단계의 예측 경사를 계산하는 하나의 방법이다.
Gradient Descent의 배치가 전체 데이터 셋인 것에 반해 확률적 경사하강법은 반복 당 하나의 예만을 사용함으로서 중요한 평균값을 추정할 수 있다는 장점이 존재한다.
반면 확률적 경사하강법은 여러 변형 함수의 최저점에 근사한 점을 찾을 수 있다는 가능성은 높으나 항상 보장되지 않으며 노이즈가 심각하다는 단점이 존재하며, 이를 극복한 것이 무작위로 선택한 10개에서 1000개 사이의 예로 구성하여 전체 배치보다 더 효율적인 형태로 나타나는 미니배치 확률적 경사하강법(Mini-batch Stochastic Gradient Descent, MBSGD)이다.
