GloVe: Global Vectors for Word Representation

GloVe: Global Vectors for Word Representation

GloVe: Global Vectors for Word Representation는 2014년에 스탠포드 대학 연구진들이 발표한 논문으로

요약

Glove는 co-occurrence(단어 - 단어 공동 등장 빈도)를 활용하여 단어의 의미를 다차원 벡터에 대입을 시키는 방식으로 임베딩 모델입니다. 해당 모델은 단어 유사도 태스크에서 75% 성능을 보였고 유사도 태스크와 개체 인식 태스크에서도 기존의 모델들의 뛰어넘는 성능을 보였다고 합니다.

개요

Semantic vector space 언어 모델에서는 각 단어들을 real-valued vector로 표현합니다. 이 벡터들은 information retrieval, 문서 분류, QA, 개체 인식 등 다양한 작업에서 사용할 수 있습니다.
대부분의 word vector 방식에서는 두 단어 벡터 간의 거리 또는 각도로 단어들의 의미를 표현하였습니다.
하지만 최근 여러 차원의 벡터로 단어들을 표현하는 방식이 소개되었습니다. 예를 들자면 '왕과 여왕' 그리고 '남자와 여자'의 관계가 동일하다는 것이 벡터 공간에서 '왕-여왕 = 남자-여자'의 식으로 나타낼 수 있는 것이죠.
단어 벡터를 표현하는 방식에는 크게 두 가지가 있습니다. LSA와 SKIP-GRAM 방식이 대표적인데 LSA는 word analogy 태스크에 약하다는 문제점이, SKIP-GRAM은 corpus의 전체적인 통계를 활용해야 하는 문제에 약하다는 문제점이 있습니다.
연구진들은 해당 논문에서 global word-word co-occurence를 활용해 학습된 specific weighted least squares 모델을 제안합니다. 해당 모델은 meaningful substructure를 가진 word vector space를 생성하며, 그를 통해 word analogy 태스크에서 75%의 정확도를 보이면서 SOTA를 달성했습니다. 또한 이 모델은 이 외에도 다양한 태스크에서 다른 모델들의 성능을 뛰어넘었다고 합니다.

The GloVe Model

Corpus 내에서 단어들의 ocuurence 통계는 word representation 학습에서 매우 중요한 정보입니다. 연구진들은 이런 Global corpus statistics를 모델에서 바로 활용할 수 있게 하는 GloVe라는 모델을 만들었습니다.
본격적으로 GloVe에 대해서 알아보기 전에 논문에서 정의한 기호 표시 몇 가지에 대해 알아보겠습니다. $X$는 word-word co-occurance count 행렬을 나타내고 $X_{ij}$는 단어 $j$가 단어 $i$와 함께 사용된 횟수입니다. $X_i$는 $\sum_kX_{ik}$로 어떤 단어가 단어 i와 함께 사용된 횟수들입니다. 마지막으로 $P_{ij}$는 $P(j|i)$로 단어 $i$가 등장했을 때 단어 $j$가 함께 등장할 확률입니다.

의미의 표현

Co-occurrence 확률에서 단어의 의미가 어떻게 추출될 수 있는지 예를 한 가지 들어보겠습니다. 단어 $i$가 ice 단어 j가 steam이라는 단어일 때 두 단어의 관계는 두 단어와 다른 단어들의 co-occurrence 확률을 통해서 표현할 수 있습니다. 만약 $k$라는 단어가 solid라는 단어라고 하면 $P_{ik}/P_{jk}$가 컨 값이 나올 것이라고 예상할 수 있습니다. 비슷하게 ice라는 단어와 연관성이 낮고 solid라는 단어와는 연관성이 높은 단어가 단어 $k$일 경우, $P_{ik}/P_{jk}$는 작은 값을 가질 것입니다. 이를 통해서 두 단어와 다른 단어의 관계를 통해서 두 단어의 관계를 알 수 있다는 것을 알 수 있습니다.
이를 통해 알게 된 두 단어의 관계를 수식으로 표현하면

$F(w_i,w_j,w_k) = \frac{P_{ik}}{P_{jk}}$(Eqn.1)

로 나타낼 수 있습니다. 이 수식의 목표는 $\frac{P_{ik}}{P_{jk}}$를 나타내는 것이고 벡터 공간은 선형구조이기 때문에 두 벡터의 차이를 이용할 수 있도록

$F(w_i-w_j,w_k)=\frac{P_{ik}}{P_{jk}}$(Eqn.2)

로 수식을 수정합니다.

또한 Eqn.2를 그대로 사용할 경우 좌변은 벡터, 우변은 스칼라인 문제가 있으므로 dot product를 사용하였고 새로운 수식은

$F((w_i-w_j)^Tw_k) = \frac{P_{ik}}{P_{jk}}$(Eqn.3)

입니다.

하지만 위의 수식에도 문제점이 하나 있습니다. 두 단어의 관계는 항상 같아야 한다는 것인데 해당 수식에서는 $\frac{P_{ik}}{P_{jk}}$와 $\frac{P_{jk}}{P_{ik}}$의 결과가 다를 수 있다는 것이죠.
따라서 연구진들은 해당 문제를 해결하기 위해 $F$가 $(R,+)$와 $(R_{>0},X)$ 사이에서 homomorphism하도록 하였습니다. Homomorphism하다는 것은 $\frac{P_{ik}}{P_{jk}}=\frac{P_{jk}}{P_{ik}}$이라는 것으로 homomorphism하면 $f(a+b)=f(a)f(b)$한 특성을 가진다고 합니다. 이를 뺄셈으로 바꾸어보면 $f(a-b)=f(a)/f(b)$로 나타낼 수 있고 이를 Eqn.3에 대입하면

$F((w_i-w_j)^Tw_k)=\frac{F(w^T_iw_k)}{F(w^T_jw_k)}$(Eqn.4)

를 얻을 수 있고 Eqn.3과 Eqn.4를 이용해

$F(w^T_iw_k)=P_{ik}=\frac{X_{ik}}{X_i}$(Eqn.5)

라는 수식을 얻을 수 있습니다.

여기에 Eqn.4에서 $F=exp()$라고 한다면

$w_i^Tw_k=log(P_{ik})=log(X_{ik})-log(X_i)$(Eqn.6)

라는 수식이 나오게 됩니다.
Eqn.6에서는 $X_i$를 제외한 값들은 모두 exchange symmetry($x_{ik}=x_{ki}$)하므로 $X_i$를 $b_i+b_k$(각각 $i$와 $k$에 대한 bias)로 대체하여 식 전체가 exchange symmetry하게 만듭니다.
이를 수식으로 나타내면

$w^T_iw_k+b_i+b_k=log(X_{ik})$(Eqn.7)

입니다.

지금까지 많은 과정을 거쳐 Eqn.1을 Eqn.7로 변환하였지만 아직 $log(x)$에서 $x=0$일 경우 값이 무한대가 된다는 문제점이 남아있습니다. 만약 어떤 단어 $i$와 $k$가 같이 등장한 적이 없을 경우 이 문제점은 치명적으로 작용할 것입니다. 따라서 $log(X_{ik})$대신 $log(1+X_{ik})$를 활용하는 것으로 이 문제를 해결하였습니다.
마지막으로 학습 과정에서 co-occurrence 값이 작은 경우와 큰 경우를 동일하게 취급하여 작은 co-occurrence(작은 co-occurence는 noisy하고 담고 있는 정보의 양이 적습니다)의 영향을 심하게 받게 되는 문제를 해결하기 위해 Eqn.7에 least square를 적용하고 가중치 $f(X_{ij})$를 더하여

$J=\sum^{V}_{i,j=1}f(X_{ij})(w^T_iw_j+b_i+b_j-logX_{ij})$(Eqn.8)

라는 수식을 구하고 이를 학습의 비용 함수로 사용합니다.

다른 모델과의 관계

단어 벡터를 비지도 학습하는 기법은 대부분 corpus의 occurrence에 기반을 하고 있습니다. 따라서 이번 파트에서는 다른 모델들 중 skip-gram과 ivLBL이 Glove와 어떤 관계가 있는지 볼 것입니다.
Skip-gram과 ivLBL 방식은 단어 $i$가 단어 $j$와 함께 등장할 확률을 $Q_{ij}$로 정의합니다.
이때 $Q_{ij}$가 소프트맥스 함수라고 가정하면

$Q_{ij}=\frac{exp(w^T_iw_j}{\sum^V_{k=1}exp(w^T_iw_k}$

입니다.

해당 모델들의 목적은 $Q_{ij}$의 확률을 최대화하는 것으로 목적 함수는

$J=-\sum_{i∈corpus,j∈context(i)}logQ_{ij}$

으로 나타낼 수 있습니다.

또한 모델이 좀 더 효율적인 학습을 할 수 있도록 $Q_{ij}$를 근사할 수 있도록 하였습니다. 하지만 like term의 수를 co-occurrence 행렬 X를 통해 구할 수 있다는 것을 이용하면

$J=-\sum^V_{i=1}sum^V_{j=1}X_{ij}logQ_{ij}$

로 나타내어 훨씬 더 효율적인 연산을 수행할 수 있습니다.

이 수식에 아까 위에서 정의했던 용어 $X_i=\sum_kX_{ik}$와 $P_{ij}=X_{ij}/X_i$를 적용하여 다시 쓰면

$J=-\sum^V_{i=1}X_i\sum^V_{j=1}P_{ij}logQ_{ij}$

로 쓸 수 있고 이 수식에 또 다시 $P_i$와 $Q_i$의 크로스 엔트로피 값을 구하는 함수를 $H(P_i,Q_i)$라고 정의한다면

$J=\sum^V_{i=1}X_iH(P_i,Q_i)$

로 나타낼 수 있습니다.

크로스 엔트로피는 꼬리가 긴 분포에서 성능이 좋지 않다는 문제점이 존재합니다. 그런데 co_ocurrence 행렬에서는 75%~95%의 데이터가 0(수 많은 단어들이 있을 때 서로 연관이 있는 단어보다는 서로 연관이 없는 단어가 훨씬 많으므로)이라고 합니다. 이렇게 되면 크로스 엔트로피의 문제점이 극대화될 것이기 때문에 이를 해결하기 위해 최소제곱법을 사용하고

$J=\sum_{i,j}X_i(P_{ij}-Q_{ij})^2$

라는 수식으로 나타냅니다.

위의 수식에서도 여전히 문제점은 존재합니다. $P_{ij}=X_{ij}, Q_{ij}=exp(w^T_iw_j)$는 정규화되지 않은 분포인데 $X_{ij}$가 종종 매우 큰 값을 가지게 되는 경우가 발생한다고 합니다. 그리고 이런 경우가 발생하면 학습 효율에 좋지 않은 영향을 미칠 수 있습니다.
따라서 $P_{ij}$와 $Q_{ij}$에 로그를 적용하여

$J=\sum_{i,j}X_i(logP_{ij}-logQ_{ij})^2=\sum_{i,j}X_i(w^T_iw_j-logX_{ij})^2$

로 수식을 수정합니다.

마지막으로 처음부터 정해진 가중치 $X_i$는 최적의 결과를 보장하지 않고 자주 등장하는 단어에 대한 가중치 데이터를 조정하는 것으로 성능을 향상시킬 수 있다는 점에 기반하여 연구진들이 만든 좀 더 general한 가중치 함수를 수식으로 나타내면

$J=\sum_{i,j}f(X_{ij})(w^T_iw_j-logX_{ij})^2$

로 나타낼 수 있고 이 수식은 위에서 등장한 Eqn.8과 동일합니다.

모델의 연산 복잡도

학습 연산의 복잡도는 co-occurrence 행렬 X에 존재하는 0이 아닌 원소의 개수에 큰 영향을 받습니다. 그렇기 때문에 0이 아닌 원소의 개수에 대한 경계를 설정할 수 있느냐가 중요합니다. 그리고 이에 앞서 co-occurence 분포에 대한 가설 몇 가지를 세우겠습니다.
1. $X_{ij}$가 각 단어 쌍의 frequency rank $r_{ij}$의 power-law 함수로 나타낼 수 있다.

$X_{ij}=\frac{k}{(r^a_{ij})}$

여기서 $X_{ij}$가 크다는 것은 동시에 등장하는 빈도가 높다는 것인데 $X_{ij}$와 $r_{ij}$는 반비례하는 관계이므로 두 단어의 co-occurrence가 높을수록 $r_{ij}$는 작아집니다.
2. Corpus의 총 단어 개수가 co-occurrence 행렬 $X$의 모든 원소의 총합에 비례할 것이다.

$|C|~\sum_{ij}X_{ij}=\sum^{|X|}_{r=1}\frac{k}{r^a}=kH_{|x|,a}$

여기서 $|X|$는 등장 빈도 순위의 최댓값으로 행렬 $X$의 0이 아닌 원소들의 개수와 같습니다. 또한 이 숫자는 $r$의 최댓값과도 동일합니다. 따라서 만약 $X_{ij}$에 0이 아닌 원소가 없다면 학습 과정에서 무시될 것입니다.
마지막으로 연구진들은 $a$ 값도 실험을 해보았는데 $a=1.25$일 때 복잡도는 $O(|C|^0.8)$로 기존 모델들의 $(|C|)$보다 더 좋은 복잡도를 가진다고 합니다.

모델 실험 결과

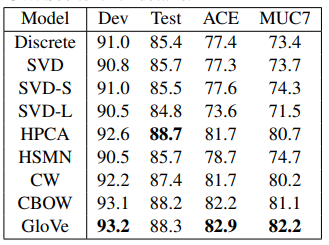
모델 성능 실험 결과 대부분의 태스크에서 기존 모델들보다 좋은 모습을 보임으로써 성능을 입증하였습니다.

후기

이번에는 GloVe라는 임베딩 모델의 논문을 읽어봤는데 내가 지금까지 본 논문 중 가장 많은 수식을 포함한 논문이었다. 수학적인 지식이 부족한 나에게는 굉장히 읽기 힘든 논문이었기 때문에 다른 분들의 해석을 많이 참고할 수밖에 없었다. 이러한 수학적 지식의 부족을 극복하기 위해서는 이런 논문에 나오는 수식들을 그냥 넘기지 말고 어떤 원리가 담겨있는지 생각하며 봐야 할 것 같다.

ps. 늘 그렇듯이 틀린 내용이 있을 수 있으므로 감안해주시고 만약 발견하신다면 댓글로 알려주시면 감사하겠습니다.