[논문리뷰 | CV] SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS (2017) Summary

9e0na·2023년 7월 19일
Computer VisionDeepLearningpaper-review
1

[논문리뷰]

목록 보기
14/42
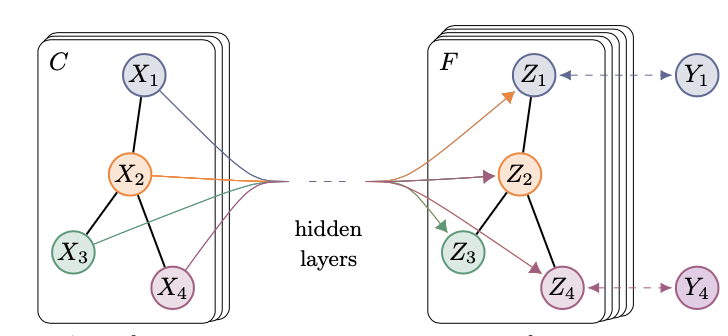
post-thumbnail

Title

  • SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
  • GCN

DSBA 연구실(윤훈상)님의 논문 리뷰를 참고하여 작성하였습니다.

0. Background

0.1. Semi-Supervised Classification

  • label data는 적고, unlabel data는 많을 때 (훈련으로 보충하고자 할 때) 사용함.
  • Target(Label)이 있다가도 없음.

0.2. Graph Neural Network

  • Graph꼴의 구조를 갖는 데이터에 대한 Neural Network
  • Graph의 기하하적 구조 때문에 Geometric Deep Learning이라고도 칭함.
  • Graph와 관련된 모든 Neural Network를 GNN

0.3. Convolution on Graph

  • CNN(Convolution Neural Network)은 이미지에 대하여 Filter를 통해 정보들을 Aggregate해 나가는 과정임.

Convolution이란?

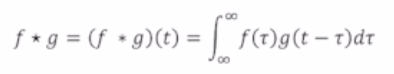
  • 두 함수의 합성곱임.
  • f,g 가운데 하나의 함수를 반전 or 전이 시킨 다음 다른 하나의 함수와 곱한 결과를 적분함.
    -> 현재의 합성곱의 값은 이전 시간의 결과를 포함함.

ex) 산에서 메아리를 한다고 하면, t시점의 소리는 이전 소리와 중첩되어 나타나는데, 아래의 예시와 같음

  • 최종 output은 맨 오른쪽의 하늘색 선과 같이 나타나게 됨.

🤜 이는 '이미지'에서만 사용되는 개념이 아님.

Graph Convolution이란?

  • Graph에 Convolution Filter을 적용해서 하나의 노드의 인접 노드와의 관계를 계산하고 싶을 때 함.
  • Convolution은 전체 data에서 Local Feature를 뽑아내는 데 매우 유용함.
  • Filter들이 Spatial location에 따라서 변하지 않음.

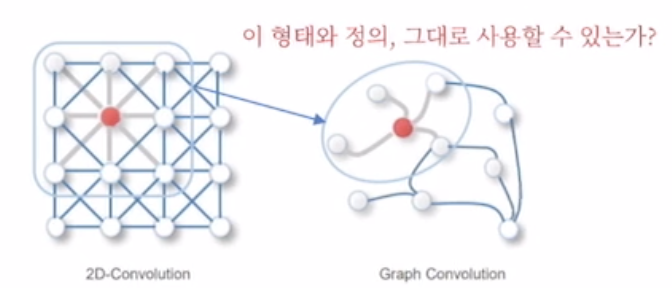
  • 이미지에서는 Grid형태로 Graph로 나타낼 수 있지만, Graph에서는 Convolution Filter가 계속해서 모양이 달라지게 됨.
  • 즉, 그래프에서의 Convolution Filter가 모든 데이터에 대하여 같은 크기가 아니기 때문에 사용 불가함.
  • Convolution = Regular Grid

하지만 어떻게든 Graph에 Convolution을 쓰고 싶으면?

Convolution Theorem

  • 한 Domain의 Convolution은 다른 Domain의 point-wise multiplication과 같음.
    🤜 즉, Graph Domain의 Conv는 Fourier Domain의 point=wise multiplication과 같음.
  • Conv의 Laplace 변환은 point-wise multiplication으로 변함.

0.3.1. CNN vs GCN

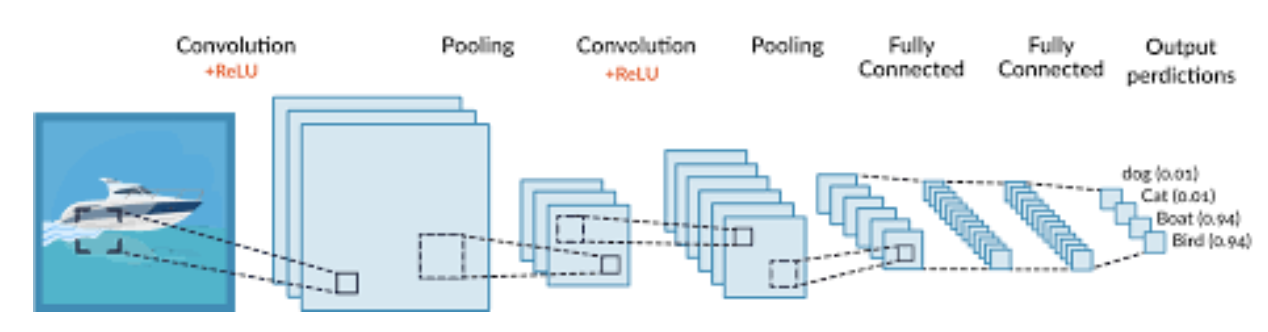
  • 합성곱 연산을 통해 각 Layer마다 weight와 filter의 값들을 스스로 update하여 학습함

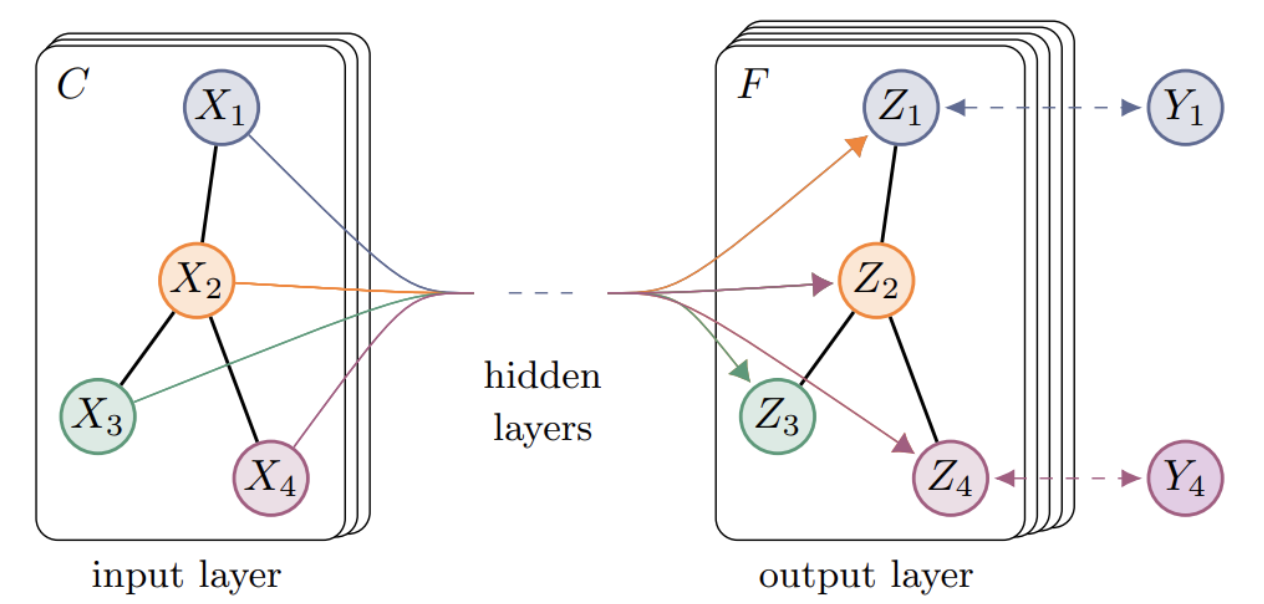
  • 각 Layer를 통과하면서 Convolution 연산을 수행하고 그래프의 특정 값을 update함.
    -> 그래프의 점(vertex) or 선(edge)가 될 수 있지만, 이 논문에서는 vertex의 feature값을 update하는 논문임.

0.4. Spectral vs Spatial (Conv)

  • Central Node의 Feature를 연삼함에 있어서 Neighbors를 이용하는 것은 같은데, 사용하는 방식이 다름.
    🤜 사용하는 관점만 다름!

Spectral Convolution

  • 이는 수학 기반이며, Graph Conv을 Graph Signal processing의 일환으로 봄.
  • Graph Signal에 대한 Noise 제거 과정으로 봄.
  • Spectral = Spectrum
  • 수학적 기반이 탄탄하게 잡혀 있어서 Spectral을 많이 사용함.

Spatial Convolution

  • 공간에 대해서 Convolution을 하겠다라는 의미임.
  • Central Node를 주위 Neighbor의 Feature로 Update 하는 과정임.

🤜 Spectral은 계산 비용이 크지만, Spatial은 크지 않음.

0.5. 꼭 알아야 할 것

주어져 있는 정보는?

  • Labeled / Unlabeled Node들이 공존해 있는 그래프
  • 각 노드들의 Feature / Edge 정보 존재

찾아야 하는 미지수는?

  • Supervised Loss를 통해 모델을 훈련시키는 과정을 거침. (Labeled)
  • 하지만 Inference할 때는 Unlabeled Data에 대해서 진행함.
  • 목적은 Labeled, Unlabeled data를 Convolution을 통해서 Node Classification or Graph Classification을 진행하는 것임.

Abstract

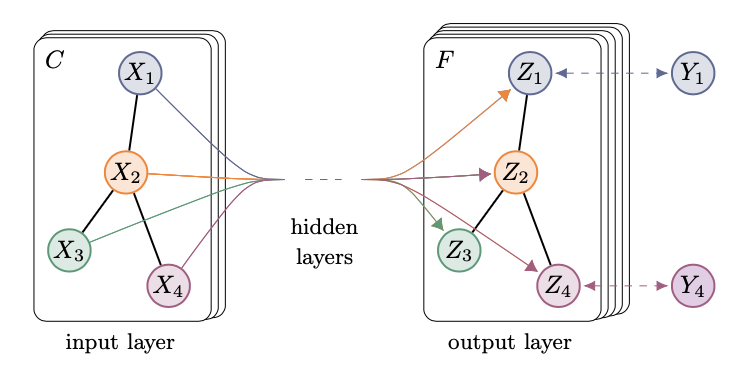
  • 이 연구는 Graph Convolution Network (GCN)에 대한 초창기 연구로, GCN은 Adjacency Matrix, Degree Matrix 또는 Feature Matrix를 활용하여 그래프를 표현하는 신경망 기법을 소개함.
  • GCN에는 두 가지 형태인 Spatial GCN과 Spectral GCN이 있으며, 이 중 본 연구는 Spectral GCN에 초점을 둠.
  • 이 연구는 Layer-wise Propagation 규칙을 간략히 소개하며, 이 규칙이 Spectral graph Convolution에 대한 효과적이고 빠른 1차 근사법이라는 것을 입증
  • 이 방법은 연결된 노드들 간의 유사성을 전제로 하므로(같은 Label을 가질 가능성이 큼), 그 이상의 다양한 정보를 포착하지 못해 모델의 성능에 제약이 생김.
  • 제시한 방법이 빠르고 효율적인(Fast Approximate Convolutions on Graph) 근사임을 증명함.
  • 그래프의 각 노드의 feature와 adjacency matrix A가 주어졌을 때, 이를 이용해 classification할 수 있는 multi-layer graph convolutional network(GCN) 즉, 𝑓(𝑋,𝐴)
    를 제시함.

1. Introduction

  • 이전의 semi-supervised 연구에서 사용되었던 loss는 '연결된 vertex간에는 유사한 label을 지닌다'고 학습되었기에 graph가 지닌 추가적 정보를 담지 못하는 한계가 존재했음.
  • 이 연구에서 소개하는 GCN(Graph Convolution Network)은 Adjacency Matrix를 입력 값으로 취하여 연결된 노드들의 관계를 직접 활용함으로써 기존의 한계를 극복함.

  • 위 수식은 그래프의 연결된 노드가 동일한 Label을 공유할 가능성이 있다는 가정에 의존하여 학습 진행하기 때문에, 모델의 능력(capacity)을 제한한다고 언급하며 GCN을 제안함.

2. Fast Approximate Convolutions on Graphs

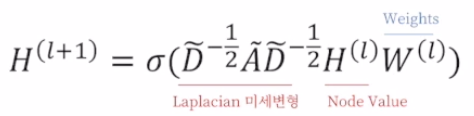
  • 본 논문에서는 Graph-based Neural Network model를 위와 같이 정의함.
  • 이는 Spectral Convolution Network를 1차 근사만으로도 계산할 수 있게 만들고 접근성이 좋음.

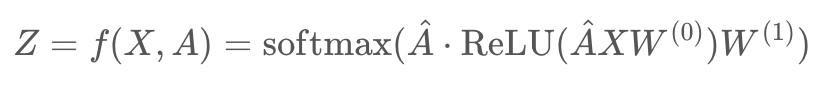
  • 위의 식이 first-order approximation of lacalized spectral filters on graph인 것을 유도하는 것이 본 논문의 핵심임.

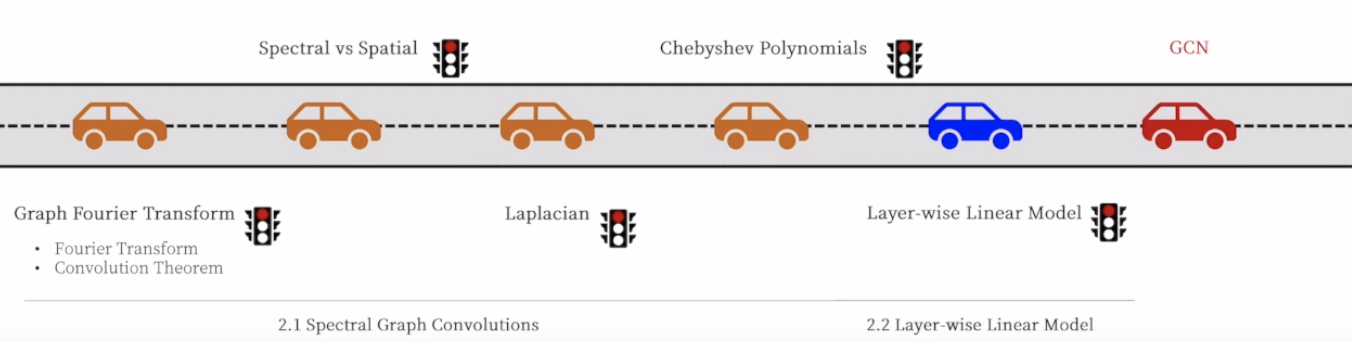
  • 위의 빨간색 친 부분을 이해하기 위해서는 위의 그림의 개념들을 다 알아야 함.

2.1. Spectral Graph Convolutions

  • Graph에서의 Spectral Convolution은 Fourier Transform을 통해 eigen-decomposition을 수행하는 것이며, 수식은 위와 같음.

2.1.1. (Graph) Fourier Transform

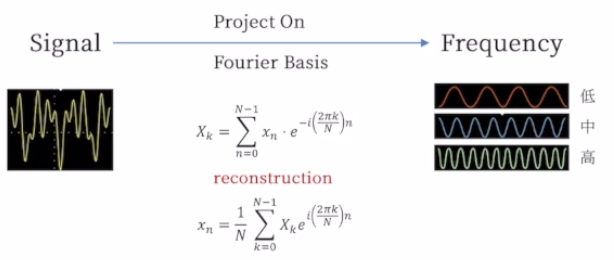
  • Signal을 Frequency별로 분행하는 과정을 의미함.
  • 이는 [Time Domain] -> [Frequency Domain]

  • Signal을 분해하는 방법은 Signal을 Fourier Basis에 Projection(사영)함.
    🤜 PCA에서 어떤 vector을 기저 vector로 사용하듯이
  • Fourier Transform은 주파수마다 Signal을 출력하는데, 이 때 주파수에는 Singal을 사영(Projection)하는 Fourier Bases가 존재함.
  • 고유 분해 즉, eigen-decomposition을 수행하여 이를 찾는 것임.

그러면 이는 그래프 푸리에 변환에서는 어떻게 적용될까?

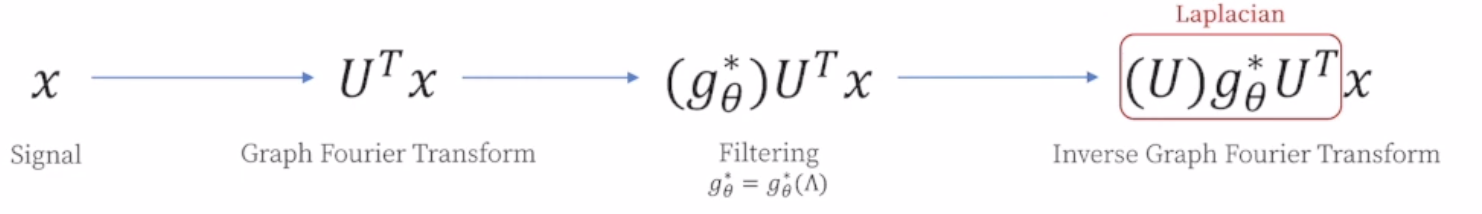
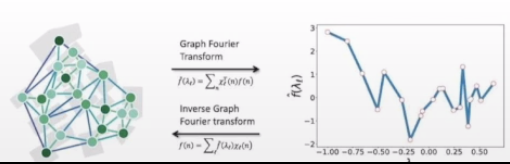
  • Graph Signal(=Feature)을 Frequency(=Feature들 간의 차이)별로 분해하는 과정임.
  • [Graph Domain] -> [Frequency Domain]

2.1.2. Spectral vs Spatial (Convolution)

  • 위에서 설명했기 때문에 pass

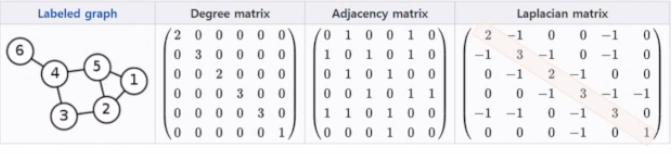
2.1.3. Laplacian Matrix

LL = DD - AA

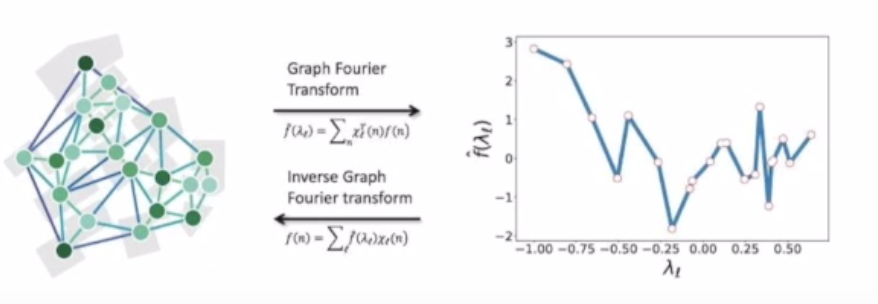
  • Laplacian Matrix는 2가지 관계를 하나의 Matrix로 규합한 것임.

  1. Degree Matrix
    : 하나의 노드가 다른 몇개의 노드와 연결되어 있는가? (대각행렬)

  2. Adjacency Matrix
    : 하나의 노드가 다른 어떤 노드와 연결되어 있는가? (비대각행렬)

  • 대각행렬과 비대각행렬의 '차'이지만, 두 행렬의 차가 값을 뺀다는 의미가 X
    -> 두 행렬을 하나의 행렬로 합친다는 의미임.

왜 Graph Fourier Transform을 적용함에 있어 Laplacian이 왜 등장할까?

  • Fourier Transform 안에 이미 Laplace operator가 포함됨.
  • 기존 Fourier Transform에도 Laplace operator가 쓰이는 것과 대응관계이고, Laplacian의 Eigen-vector가 Fourier Basis 역할을 수행함.
  • Laplacian을 Feature Vector에 곱하는 것이 Fourier Transform의 역할을 함.

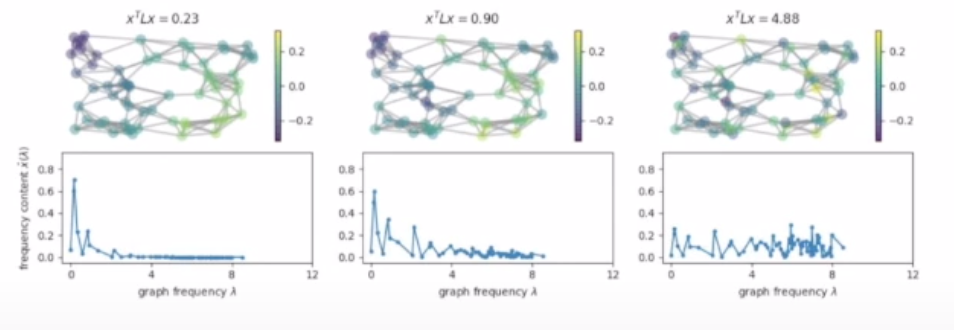
2.1.4. Fourier Transform Check

  • Graph Fourier Transform을 통해 Frequency가 낮은 관계들을 우선적으로 반영함.
  • Laplacian Matrix의 적용 자체가 Convolution임.
  • Signal: Node Feature
  • Frequency: Central Node와 Neighbor node간의 차이 (Laplacian으로 구함)

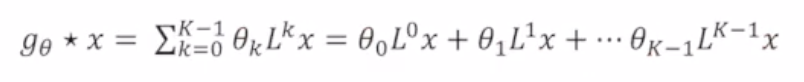
2.1.5. Localized Filtering

2.1.6. Chebyshev Polynomial

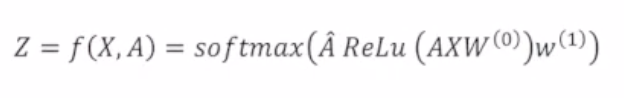
  • 문제점: 해당 식은 Computationally Expensive함. -> 근사식 활용

2.2. Layer-Wise Linear Model

  • GCN은 결국 Chebyshev Polynomial의 K를 1로 변환한 뒤, 해당 과정을 Layer로 표현함

3. Semi-supervised Node Classification

  • 이처럼 많은 trick을 가한 후 최종적으로 ZZ
    를 Deep Learning form으로 변환하면 다음과 같음.

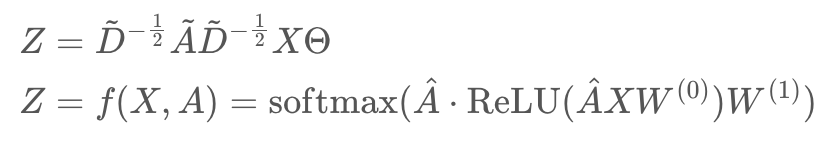
  • 위 수식을 통해 two-layer GCN을 구성할 수 있음.

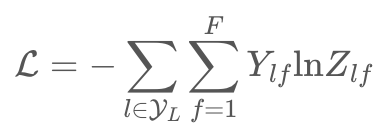
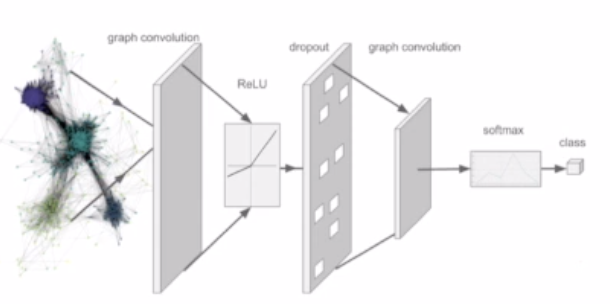
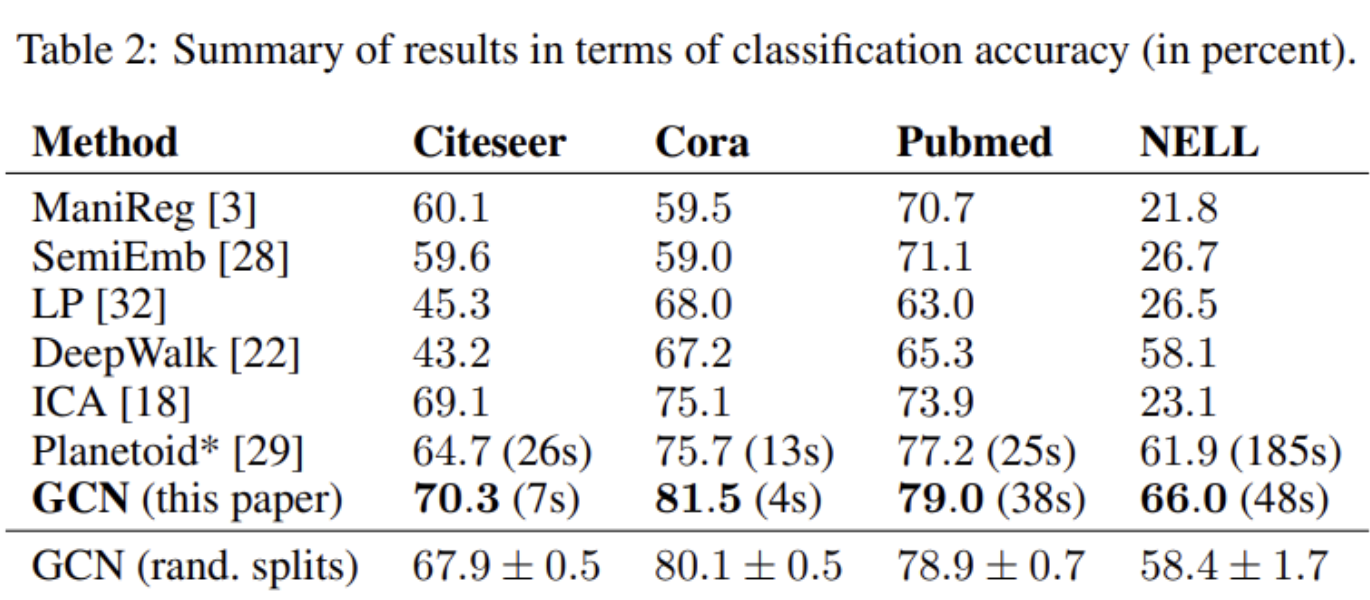
4. Experiments

  • Node는 논문을 사용하였고, Egde는 논문들 간의 인용을 의미함.
  • Label rate는 각 데이터셋에서 훈련에 사용되는 node를 전체 노드 개수로 나눈 비율을 의미하며, Node Feature와 Label은 각각 Bag of Words, Node Label을 의미함.

  • 기존 논문에서 제안한 모델들 보다 본 논문에서 제안하는 GCN의 성능이 우수한 것을 확인

업로드중..

  • 위 그림은 Chebyshev filter를 2차, 3차 다항식으로 계산한 값과, 1st-order model을 한 경우와 single parameter, Renormalization trick을 사용한 경우와 비교한 결과 Renormalization trick을 사용한 경우 가장 우수한 성능을 보임.

5. Results

  • pass

6. Future Work

Memory Requirement

Directed edges and edge features

Limiting assumptions

7. Conclusion

  • 이 연구에서는 그래프 구조 데이터에 대한 준지도 학습 분류를 위한 새로운 방법을 소개함.
  • 제안된 GCN 모델은 그래프 상의 스펙트럼 합성의 1차 근사에 기반한 효율적인 계층별 전파 규칙을 사용
  • 다양한 네트워크 데이터세트에서의 실험 결과, 이 GCN 모델은 준지도 분류에 유용한 방식으로 그래프 구조와 노드 특징을 모두 인코딩할 수 있음을 보여줌.
  • 이러한 설정에서, 이 모델은 최근에 제안된 여러 방법들을 크게 앞선 성능으로 보여주면서도 계산적으로 효율적임.

🎯 Summary

  1. 저자가 뭘 해내고 싶어 했는가?
  1. 이 연구의 접근 방식에서 중요한 요소는 무엇인가?

  1. 그래프의 각 노드의 feature와 adjacency matrix A가 주어졌을 때, 이를 이용해 classification할 수 있는 multi-layer graph convolutional network(GCN) 즉, 𝑓(𝑋,𝐴)를 제시

  2. 제시한 방법이 빠르고 효율적인(Fast Approximate Convolutions on Graph) 근사임을 증명함.

  3. 이전의 semi-supervised 연구에서 사용되었던 loss는 “연결된 vertex간에는 유사한 label을 지닌다”고 학습되었기에 graph가 지닌 추가적 정보를 담지 못하는 한계가 존재했음. 본 논문에서 제시한 GCN은 adjacency matrix를 입력에 사용함으로써 이에 대한 제한을 해결함.

  1. 어느 프로젝트에 적용할 수 있는가?
  1. 참고하고 싶은 다른 레퍼런스에는 어떤 것이 있는가?
  1. 느낀점은?

📚 References

Youtube

Blog

profile
9e0na
디지털 마케터가 되기 위해 [a-zA-Z]까지 정리하는 거나입니다 😊
다음 포스트

[논문리뷰 | CV] MobileNet: Efficient Convolutional Neural Networks for Mobile Vision Applications (2017) Summary

0개의 댓글