선형대수학 챕터는 다루는 개념이 많아서 포스팅을 나누려고 합니다.
이번 챕터에서 가장 중요한 개념은 아래 3가지입니다.
- LU 분해 (LU decomposition)
- 고유벡터와 고유 값
- 특이값 분해(SVD)
선형 방정식이란?
선형 방정식 (linear)
- 직선으로 나타낼 수 있는 방정식
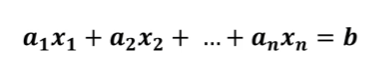
비선형 방정식 (non-linear)
- 직선으로 나타낼 수 없는 방정식 (예를 들어서, x^2 + x^4 = 5 이런 것)
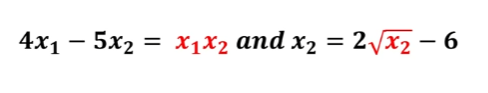
선형 방정식 계 ? (linear system)
-
같은 변수들을 포함하는 선형 방정식이 1개 이상 있는 집합
-
아래 두 선형 방정식은 선형 방정식 계라고 할 수 있음
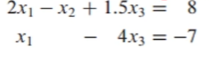
-
방정식 계는 해의 집합에 따라 2 종류로 나눌 수 있음
(1) Inconsistent : no solution. (해가 없는 경우)
(2) Consistent : exactly one solution, infinitely many solution. (해가 1개인 경우, 해가 무수히 많은 경우)
선형에서는 위처럼 3개 상황밖에 존재하지 않음.
즉, 만일 해가 2개 존재한다는 건 비선형이라는 거임
해의 집합 ? (solution set)
- 선형 시스템에서 가능한 모든 해의 집합
상등 ?
- 두 선형 시스템이 같은 solution set을 갖고 있다면, 두 선형 시스템은 상등하다고 함
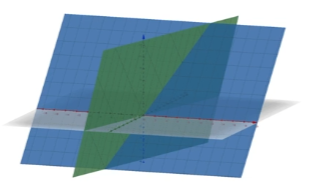
- 아래 그림처럼 두 선형 시스템(두 평면)은 같은 solution set(맞닿은 선)을 갖고 있으므로, 상등함 (이해한게 틀렸다면 알려주세요..!)
선형 방정식 표기법
행렬 표기법
- 선형 시스템을 행렬로 표현
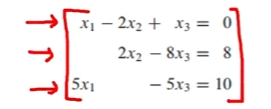
예를 들어서, 엑셀에 (키, 몸무게, 발사이즈) 라는 3개의 컬럼이 있다면,
행렬로
키 몸무게 발사이즈
[180, 80, 260] 으로 표현할 수 있는 것임
계수 행렬?

첨가 행렬?

소거법 (Elimination)
소거법이란 해를 찾아가는 방법 중 하나입니다.
개념
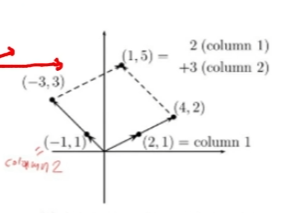
열 관점으로 풀기 (n=2 일 때, 즉 변수가 x,y로 2가지일 때)
- (2,1) 벡터와 (-1,1) 벡터에 각각 몇을 곱해야 (1,5) 좌표에 도달하는지 찾는 과정과 동일해짐
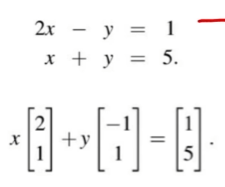
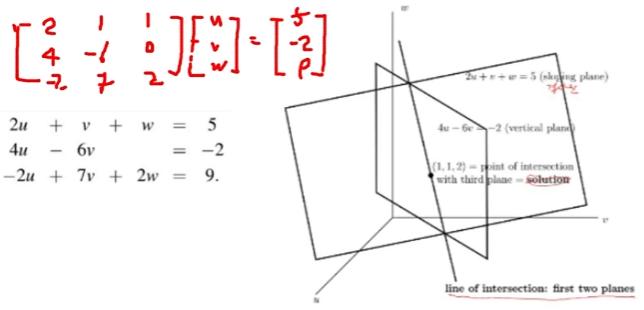
행 관점으로 풀기 (n=3 일 때)
- 행 관점으로 접근하면 3차 방정식 2개와 2차 방정식 1개를 도출할 수 있고, 즉 두 평면과 하나의 직선이 교차하는 해 (1,1,2)를 찾을 수 있음
- 연립 방정식 등 활용 가능
열 관점으로 풀기 (n=3 일 때)
- 벡터들의 상수배를 조합하여 해를 찾아갈 수 있음
- 즉, 조건을 만족하는 특정한 상수배(스칼라) = 해

가우스 소거법 소개
가우스 소거법에서 할 수 있는 기본 행 연산은 아래와 같습니다.
- 0이 아닌 상수를 행에 곱할 수 있음 (scaling)
- 두 행을 교환할 수 있음 (interchange)
- 한 행을 상수배하여 다른 행에 더할 수 있음 (replacement)
즉, 아래 그림에서 볼 수 있듯이,
1번에선 3을 곱하였고(scaling), 2번에선 두 행을 더함으로써(replacement),
변수 x를 소거할 수 있음
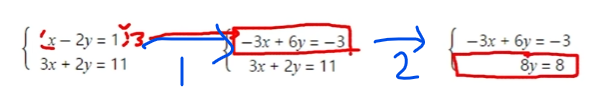
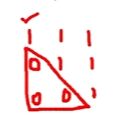
-> 이 말은 즉슨, 상/하 삼각행렬을 만들면 해를 찾을 수 있음
(스칼라가 0이면 변수가 소거되고, 아래 또는 위에서부터 변수가 하나씩 도출되므로)
가우스 소거법 단계
(1) 선형 방정식 계를 행렬로 표현하기
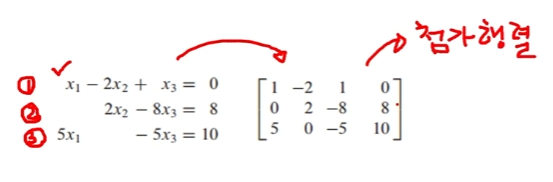
(2) 행의 계수를 0으로 만들기 (중학교때 배운 2,3차 연립방정식 풀이 과정과 동일)


(3) 상삼각행렬 완성!
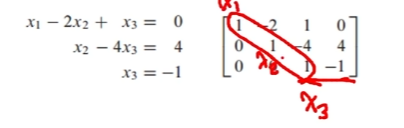
(4) x3을 알았으므로, 대입을 해서 x1, x2를 구하면 됨!
다음 포스팅에 이어서...
