역행렬이 데이터 분석에 중요한 이유
- 역행렬이 있다 = 해가 존재한다 는 의미
- 데이터 분석에서는 종종 여러 변수들 간의 관계를 설명하는 선형 방정식을 다룸.
예를 들어, 선형 회귀 모델은 종속 변수 𝑦 와 여러 독립 변수 𝑋 간의 관계를 설명함.
이 때, 선형 방정식을 해결하기 위해서는 행렬을 사용하여 문제를 표현하게 되는데, 그 행렬을 통해 𝑋에 대한 계수들을 계산할 수 있음.
즉, 만약 행렬이 가역(즉, 역행렬이 존재)하다면, 역행렬을 이용해 해당 계수를 구할 수 있습니다. (= X와 y간의 어떤 관계가 있는지 파악할 수 있습니다.)
그리고, 역행렬이 존재한다는 것은 유일한 해가 존재함을 의미합니다.

요약하자면,
역행렬을 구하면 x의 값을 바로 알아낼 수 있기 때문
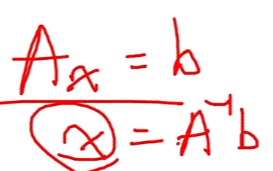
역행렬이 있는지 판단하는 방법
- ad-bc != 0 이면 역행렬이 존재함 (determinant가 0인지 아닌지 확인)
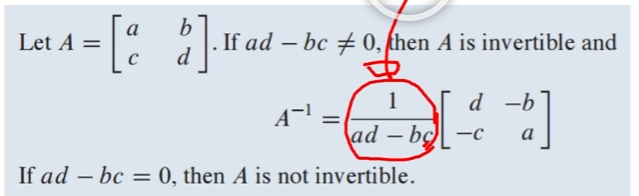
주의사항

A가 invertible 이면, A의 Transpose도 invertible

기본 행렬
기본 행렬?
- 기본 행렬은 항등 행렬(대각선만 1이고 나머진 0인 그 행렬)에 단일 기본 행 연산을 적용해서 얻을 수 있음
단일 기본 행 연산?
replacement, interchange, scaling
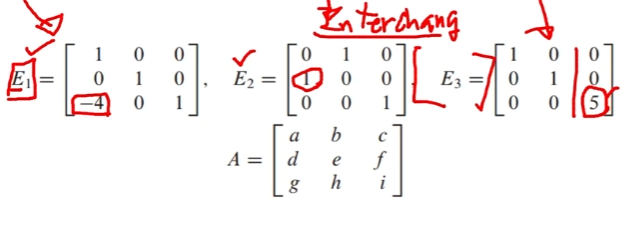
기본 행렬의 특징
-
mxn 행렬에 기본 행 연산을 할 수 있다는 것은, 어떤 mxm 행렬이 존재한다는 의미
(행렬에 기본 행 연산을 하기 위해선, 기본적으로 mxm 행렬이 존재해야 가능하기 때문) -
행렬 E가 invertible이면(역행렬이 있으면), E의 역행렬은 E를 I(단위행렬)로 변환하는 기본 행렬임
역행렬을 찾는 알고리즘

위 사진에서는 행렬 A의 역행렬 (A⁻¹) 을 구하는 과정을 설명합니다.
일단, 행렬 A와 단위행렬 I를 붙여 확장행렬(3x6)을 만들었습니다.
알고리즘 요약:
행렬 A를 단위 행렬로 변형하는 과정에서, I 역시 변형되는데, 이때 변형된 I가 A의 역행렬(A⁻¹) 이 되는 것입니다.
첫 번째 행렬 -> 두 번째 행렬:
1행과 2행을 Interchange 해주었음
두 번째 행렬 -> 세 번째 행렬:
1행에 -4를 곱한 후, 3행에 더해주었음
세 번째 행렬 -> 네 번째 행렬:
2행에 3을 곱한 후, 3행에 더해주었음
네 번째 행렬 -> 다섯 번째 행렬:
3행에 1/2를 곱해주었음
.. 위와 같은 방식으로 A를 단위행렬로 만들다 보면, I가 A의 역행렬로 변형됨!!!
이렇게 구한 역행렬로..
Ax=b 라는 선형방정식이 있을 때,
x= b(A⁻¹)이므로,
b에 역행렬을 곱하면 해(x)를 바로 구할 수 있음!!!
역행렬의 특징
행렬 A가 invertible이면 아래 만족을 모두 만족함

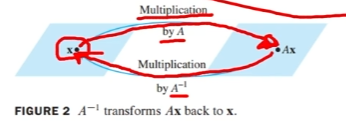
역선형 변환
공간 1에 있는 좌표값 x에 행렬 A를 곱해서 좌표값 x를 공간 2 기준의 좌표(x')로 변형했다면,
반대로 공간 2에 있는 좌표(x') 에 역행렬(A⁻¹) 을 곱해서 다시 공간 1의 좌표 x로 되돌릴 수 있음
유니티에서 오브젝트 공간/월드 공간/카메라 공간의 좌표를 각각 변형할 때 행렬/역행렬 주구장창 썼었는데 이게 역선형변환 이라는 개념이구나 하고 이마를 탁 침
🔵 흥미로웠던 점 :
위에도 썼지만, 유니티에서 그래픽 파이프라인 공부하면서 쉐이더 작성할 때 공간별 좌표를 변환하는 부분에 행렬을 썼었음. 이때의 지식이 오늘 공부를 이해하는 데에 꽤나 큰 도움이 되어서, 역시 수학은 알아두면 이득이구나 생각함.
🔵 다음 학습 계획 :
LU 분해가 무엇인지부터 배울 예정입니다.
