'분해'란?
하나의 행렬을 두개 이상의 행렬 곱으로 표현하는 식을 의미합니다.
LU 분해란?
Ax=b와 같은 선형 방정식에서 A행렬을 L(=하삼각행렬), U(=상삼각행렬)로 분해하는 방식을 의미합니다.
단, 하삼각행렬의 대각성분은 1이어야 합니다.
LU 분해를 하는 이유?
요약 :
A를 L(=하삼각행렬), U(=상삼각행렬)로 분리하면, x의 해를 찾는 데에 더욱 편리해짐
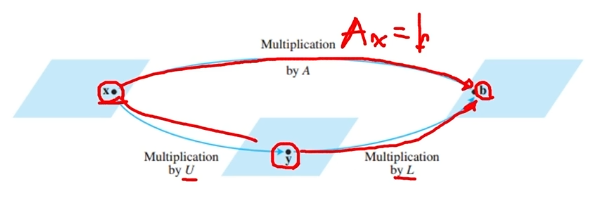
(1) Ax=b에서, A를 L과 U로 분리하기
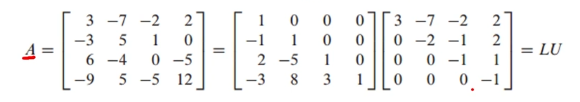
b의 값은 아래와 같음
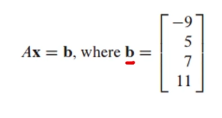
<해 구하는 과정 1️⃣,2️⃣>
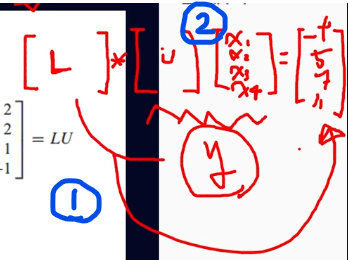
(2) <해 구하는 과정 1️⃣,2️⃣>의 1️⃣ : Ly = b에서 y값 구하기
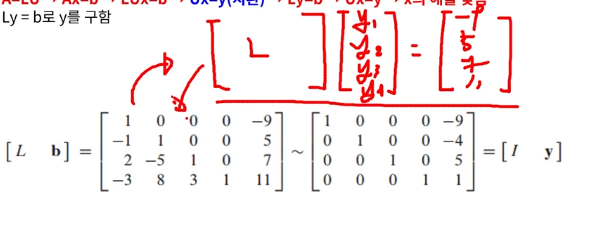
L은 대각성분이 1이므로, L행렬과 b값을 통해 L행렬의 가장 윗 행부터 y1, y2, y3, y4값을 쉽게 구할 수 있음
(3) <해 구하는 과정 1️⃣,2️⃣>의 2️⃣ : Ux = y에서 x값 구하기
U와 x1,x2,x3,x4의 곱 = (2)에서 구한 y1, y2, y3, y4
U는 삼상각행렬이므로, 여기서도 x1,x2,x3,x4를 쉽게 구할 수 있음
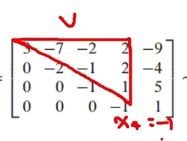
(4) Ux= y에서 구한 x값이 곧 해!
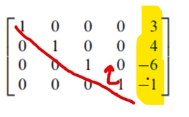
LU 구하는 방법 (LU 분해 알고리즘)
(1) 아래와 같이 3x3 행렬 A가 있다고 가정합니다.
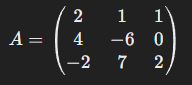
이 행렬 A를 LU분해하여 A= LxU로 표현할 것입니다.
(2) 가우스 소거법으로 U 구하기
행렬 A를 U(=상삼각행렬)로 변환합니다. 목표는 A의 대각선 아래의 요소들을 0으로 만드는 것입니다.
첫 번째 열을 0으로 만들기
1. 두 번째 행에서 첫 번째 행의 2배를 뺍니다.
R2 = R2 - 2R1 = (4 -6 0) -2x(2 1 1) = (0 -8 -2)
- 세 번째 행에서 첫 번째 행의 1배를 더합니다.
R3 = R3 + R1 = (-2 7 2) + (2 1 1) = (0 8 3)
그 결과, 행렬은 다음과 같이 변합니다.

두 번째 열을 0으로 만들기
1. 세 번째 행에서 두 번째 행의 -1배를 더합니다.
R3 = R3 + (-R2) = (0 8 3) + (0 -8 -2) = (0 0 1)
최종적으로 행렬 U는 다음과 같은 상삼각행렬이 됩니다.
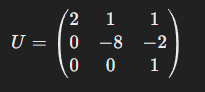
(3)-1 L행렬 구하는 방법 1
위 (2)에서 사용한 행 연산을 L행렬에 기록해보겠습니다.
첫 번째 행
첫 번재 행은 U행렬을 구하기 위한 가우스 소거법에서 그대로 둡니다. 따라서, L의 첫 번재 행렬은 (1,0,0) 입니다.
- 첫 번째 행은 기준 행으로서 다른 행들을 변형하는데 사용하지, 자신은 변형하지 않습니다.
- 따라서, L의 첫 번째 행은 '스스로 변형되지 않았음'을 의미하므로, 1열은 1, 나머지는 0이 됩니다. (=대각 성분의 첫 시작이 됨)두 번째 행
두 번째 행은 첫 번째 행의 -2배를 하여 더했으므로, L의 두 번째 행의 첫 번째 열의 요소는 -2가 됩니다.
두 번째 행은 스스로에 대한 변형을 하지 않았기 때문에 두 번째 열의 요소는 1입니다.
따라서, L의 두 번째 행렬은 (-2, 1, 0) 입니다.
세 번째 행
세 번째 행은 첫 번째 행의 1배를 더해 수정했고, 두 번째 행의 -1배를 더해 수정했습니다. 따라서, L의 세 번째 행의 첫 번째 열의 요소는 1, 두 번째 열의 요소는 -1이 됩니다.
그리고 세 번째 행은 스스로에 대해 변형하지 않으므로 대각선 원소는 1입니다.
위와 같은 방식으로 L과 U를 구할 수 있습니다,,
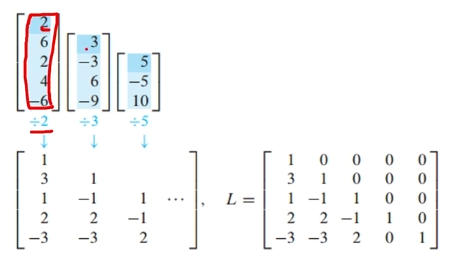
(3)-2 L행렬 구하는 방법 2
(1),(2)와 다른 행렬 A를 가져왔습니다.

각 열을 모두 0으로 만들어 주는 작업을 하면서 나오는 산출물들에 pivot 아래의 entry를 나눠주면 된다는 건데, 무슨 말이냐면,
첫 번째 열을 0으로 만들기 전의 (2 6 2 4 -6)에, 첫 번째 요소인 2를 나눠주면 L의 첫 번째 열이 나오고,
첫 번째 열을 0으로 만든 후, 두 번째 열의 두 번째 행부터인 (3, -3, 6, -9)에, 3을 나눠주면 L의 두 번째 열이 나오고,
두 번째 열을 0으로 만든 후, 세 번째 행부터인 ...
를 반복해서 L을 얻을 수 있습니다.
LU 분해 특징
- A의 역행렬로 해를 구할 때보다 연산량이 1/3배로 적음!
- A의 역행렬에 비해 메모리 저장에 효율적임
- 이유 :
(A가 sparse(대부분 0으로 채워졌을 때))
A의 역행렬 : 0이 아닌 값이 대부분일 확률이 있음
LU 분해 : L과 U도 sparse함
다음 포스팅에서 계속..
