계수 (Rank, Pivot, Null space)
-
행렬의 Rank란, 행렬의 dimension을 의미함
-
만일, 행렬은 x,y,z차원이지만 A행렬로는 x,y밖에 표현을 못 한다면, Rank=2이고 Null space=1이라고 함
-
이게 무슨 말이냐 하면, rank == pivot column의 수 라는 말임
-
그렇다면 pivot column이 무슨 말이냐?? 아래 그림 보면 바로 알 수 있음
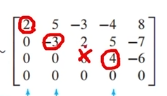
위의 행렬에서 대각 성분에 값이 있는 컬럼(=pivot column)은 3개 임. -
따라서, 위 행렬의 null space = 2 (= free variable이 x3, x5)임
determinant
determinant의 역할
(1) 역행렬이 존재하는지 알려줌
- 행렬식 != 0 : 역행렬이 존재함
- 행렬식 == 0 : 역행렬이 존재하지 않음
(2) "행렬이 변환하는 공간"의 크기 변화를 알려줌
- 2x2 행렬을 예로 들면, 이 행렬이 2차원 평면의 한 사각형을 변형했을 때, 그 사각형의 넓이가 얼마나 변하는지를 알려줌
- Determinant == 1 : 변형 전과 변형 후의 넓이가 같음
- Determinant == 2 : 넓이가 2배로 커졌음
- Determinant == 0 : 넓이가 아예 0이 되어, 평면이 한 선으로 눌렸음
determinant 구하는 방법 (2x2)
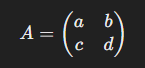
위와 같은 행렬이 있다고 할 때,
det(A) = ad - bc
determinant 구하는 방법 (3x3)
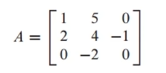
위와 같은 행렬이 있다고 할 때,
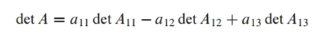
여기서 det(A11), det(A12), det(A13) 이란 각각 sub matrix를 뜻함.
예를 들어, det(A11)은 A의 1행과 1열을 제외한 sub matrix
풀이 예시
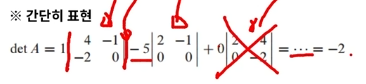
Cofactor (여인수)
여인수 전개(cofactor expansion)을 통해서 determinant를 다양한 형태로 표현할 수 있습니다.
Cofactor(여인수) 란?
Cofactor(여인수) 는 행렬의 특정 원소에 해당하는 값으로, 그 원소가 행렬의 행렬식(determinant)에 미치는 영향을 계산하는 도구라고 생각하면 됩니다.

Cofactor expansion(여인수 전개) 란?
Cofactor Expansion(여인수 전개) 는 특정 행 또는 열을 기준으로 그 행렬의 행렬식을 계산하는 방법입니다.
즉, 행렬의 행렬식을 작은 부분들(cofactor)로 쪼개서 계산하는 과정입니다.
2x2 행렬의 경우
2x2 행렬의 determinant는 보통
det(A)=ad−bc로 나타내는데, 이런 간단한 경우에는 cofactor가 필요하지 않습니다.
그러나 큰 행렬로 가면 더 복잡해지기 때문에 cofactor를 사용하여 이 과정을 해결할 수 있습니다.
3x3 행렬의 경우
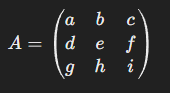
이 행렬의 행렬식은, 첫 번째 행의 각 원소 a, b, c 에 대해 각각의 cofactor를 계산하여 구할 수 있습니다.
(1) a의 cofactor 구하기
a의 cofactor를 계산하려면 a가 있는 첫 번째 행과 첫 번째 열을 지우고 남은 2x2 행렬의 determinant를 계산합니다.
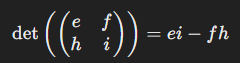
이때, 첫 번째 원소의 부호는 양(+)이므로, a의 cofactor는 a x (ei - fj)가 됩니다.
(2) b의 cofactor 구하기
b의 cofactor도 (1)과 동일하게 구하지만, 두 번째 원소의 부호는 음(-)이므로,
b의 cofactor는 -b x (di - fg) 입니다.
(3) c의 cofactor도 동일하게 구해줍니다.
이제 이 cofactor들을 모두 더해주면, 전체 행렬식이 나옵니다.
det(A) = a(ei-fj) -b(di-fg) +c(dh-eg)cofactor는 필요에 따라 Spare한 row나 column을 선택해서 계산할 수 있습니다!!
즉, 0을 포함하는 row나 column을 선택해서 위보다 빠르게 계산할 수 있습니다!! 굿~
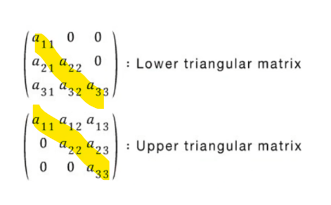
삼각행렬의 행렬식은? (더 간단함)
삼각행렬의 determinant = 대각 성분끼리의 곱!
끝임!
아래 사진을 예시로 들면,
det(A) = a11 x a22 x a33
다음 포스팅에 이어서...
