고유벡터와 고유값이란?
행렬은 벡터를 변환시키는 작업을 합니다. 예를 들어, 2차원 평면에서 행렬을 사용하면 벡터의 길이를 늘이거나 줄이고, 방향을 바꾸거나 회전시킬 수 있습니다.
하지만, 모든 벡터의 방향이 바뀌는 것은 아닙니다.
행렬을 곱해도 방향이 변하지 않는 특수한 벡터 들이 존재하는데, 이를 고유벡터라고 합니다.
예를 들어서, 벡터 v에 행렬 A를 곱했는데, 결과값이 v와 같은 방향의 벡터라면, v는 고유벡터입니다.
그리고 v의 길이가 얼마나 늘어났는지/줄어들었는지 나타내는 값이 고유값입니다.
예를 들어, 행렬 A에 고유 벡터 v(2,1)을 곱했을 때의 결과 v'가 (4,2)라면,
고유벡터가 (2,1)이므로 고유값은 2입니다.
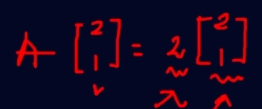
고유벡터가 행렬에 미치는 역할
행렬이 벡터를 어떻게 변환하는지 간단히 설명해줍니다.
고유벡터와 고유값이 데이터 분석에서 중요한 이유?
데이터 분석과 머신러닝
PCA(주성분 분석) 라는 차원 축소 기법에서 고유값과 고유벡터 개념이 필수적이라고 합니다. PCA는 데이터를 더 작은 차원으로 변환할 때 가장 중요한 방향(고유벡터)들을 찾고, 그 방향에 따른 데이터 변동성(고유값)을 분석하는 방법입니다.
고유 공간
간단히 말하면, 행렬 A의 특정 고유값에 대한 고유 벡터들을 모두 모아놓은 공간입니다.
고유 공간은 제로 벡터도 포함합니다.
그림으로 보면,
만약 고유값=2인 고유 공간이 주어졌다고 가정할 때,
고유 공간에 존재하는 임의의 벡터들을 선택해서 행렬 A를 곱하면, 각 벡터의 크기가 2씩 늘어난다는 뜻입니다.
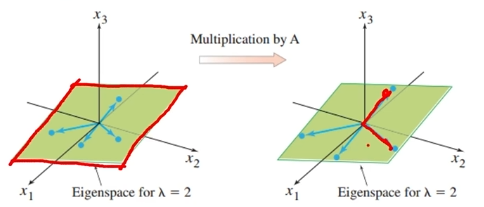
고유 공간 구하는 방법
행렬 A가 다음과 같을 때, 고유값=2에 해당하는 고유 공간(=고유 벡터들)을 찾아보자~
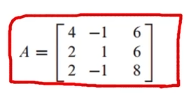
고유값=2일 때이므로, (A-2I)x = 0을 풀면 됩니다.
식만 보면 뭔 소린지 모르겠으니까, 한 단계씩 풀어보겠습니다.
(1) 먼저, A-2I 구하기 (I는 단위벡터 맞음)
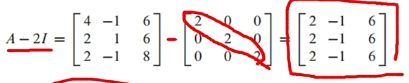
(2) 가우스 계산으로 free variable 구하기 (대각 성분이 0인 요소)
(free variable가 있다 == 고유 벡터가 있다)
여기선 x2와 x3가 free variable 이라는 것을 알 수 있습니다.
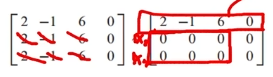
(3) (free하지 않은 x = free한 x들)의 형태로 식 나타내기
위(2)의 결과에 따르면, 2x1 -x2 +6x3 = 0 이므로,
2(x1) = (x2) - 6(x3),
x1 = 1/2(x2) - 3(x3) 으로 나타낼 수 있습니다.
즉,

위와 같은 해를
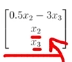
위와 같이 변형할 수 있다는 말이고,
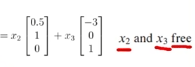
이를 x2와 x3의 합 형식으로 변형하면 위 이미지와 같습니다.
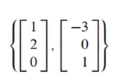
결론적으로, 두 개의 벡터(1,2,0), (-3,0,1)은 서로 독립적인 벡터이며, 고유 벡터입니다.
삼상각행렬의 고유값
삼상각행렬의 고유값은 대각 성분(diagonal term)입니다.
왜 그러냐면...
고유 벡터가 존재한다는 말은, free variable이 존재한다는 말이므로, pivot position(대각 성분)이 0이 되어야 합니다.
따라서, 아래 그림에 따라 고유값은 a11 또는 a22 또는 a33이 될 수 있습니다.
고유값의 개수는 n개(열의 개수) 이하, 즉 여기서는 3개 이하가 되어야 합니다.
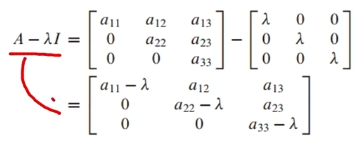
하삼각행렬의 고유값
행렬이 고유 벡터를 갖는지 알기 위해선, 행렬과 행렬의 T(Transpose)가 동일한 고유값을 갖고 있음을 증명하면 됩니다.
그런데 하삼각행렬의 T(Transpose)는 삼상각행렬입니다.
즉, 삼상각행렬의 고유값(=대각 성분)을 구하면 되는 것입니다.
게다가 T(Transpose)를 하여도 대각 성분은 변하지 않습니다. 굿
다음 포스팅에서 계속...
혹시 틀린 설명이 있다면 꼭 댓글로 알려주세요 감사합니다😀
