특성 방정식

특성 방정식은 det(A-고유값) = 0 임을 의미합니다.
즉, free variable이 존재함(자명한 해가 없음)을 의미합니다.
그래서 임의의 변수 '람다'가 특성 방정식을 만족하면, '람다'는 행렬A의 고유값이라고 할 수 있습니다.
사실 저번 포스팅에서 설명한 부분과 겹칩니다.

유사도 (Similarity)

n차 방정식에서 고유값(eigenvalue)을 찾는 것은 쉽지 않기 때문에, similarity를 주로 사용합니다.
쉽게 말하면, 비슷한 행렬을 찾아서 고유값을 찾는 개념이라고 합니다. (하지만 고유 공간은 보통 다름)

행렬 A와 행렬 B가 동일한 특성 polynomial을 갖고 있으면, 두 행렬은 동일한 고유값을 갖는다고 합니다.

이렇게만 보면 무슨 말인지 모르겠으니 쉽게 풀어서 설명하겠습니다.

polynomial = 다항식

즉, 두 개의 행렬이 동일한 다항식으로 표현되면 된다는 말입니다.
하나의 행렬이 free variable을 가지려면, determinant(행렬식)이 0이 되어야 합니다.

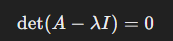
이 식을 전개하면, 𝜆에 대한 다항식이 나옵니다. 이것이 특성 다항식(Characteristic polynomial)입니다.

이 다항식의 해가 바로 행렬의 고유값인 것이고, 따라서 이 다항식이 동일하면 두 행렬은 동일한 고유값을 갖게 되는 것입니다.

---

다음 포스팅에 계속 ...