Introduction

2014년 Ian Goodfellow(.et al)은 Generative Adversarial Networks(줄여서 GAN)라는 생성 모델을 훈련하는 방법을 제시했다.

논문에서 중요한 내용은 두 가지로 나눌 수 있다.
1. GAN에 대한 이론적인 개념 제시(minimax probelm)
2. GAN이 풀어야하는 problem이 global minimum에서 unique solution을 갖고 어떤 조건을 만족하면 해당 solution으로 수렴한다는 것을 증명.

"Adversarial" 적대적이라는 단어가 왜 쓰이는지 직관적으로 알아보자.

GAN?

GAN은 기본적으로 두 개의 다른 신경망(Generator와 Discriminator)간의 적대적인 관계로 대립(Adversarial)하며 서로의 성능을 점차 개선해 나가는 것이다.

• 생성 모델 G : 데이터의 분포를 학습하는 모델
• 판별 모델 D : 이미지를 실제(학습을 진행할 때 사용하는 Training Data) 또는 가짜(임의로 만든 Generated Data)인지 분류하는 모델

Generator는 훈련 데이터의 분포를 학습하여, 임의의 노이즈를 입력으로 받아 신경망을 사용하여 이미지를 생성한다.(와우 이미지를 생성!!)
Generator의 목표는 판별자를 속여서 생성된 이미지가 실제라고 생각하도록 하는 것이다.

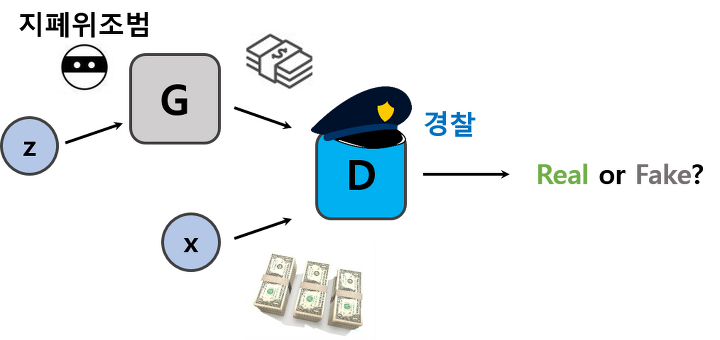
마치 두 모델이 지폐위조범(Generator)와 경찰(Discriminator)같지 않은가?

지폐위조범(Generator)은 경찰을 최대한 열심히 속이려고 하고 다른 한편에서는 경찰(Discriminator)이 이렇게 위조된 지폐를 진짜와 감별하려고(Classify) 노력한다.
이런 경쟁 속에서 두 그룹 모두 속이고 구별하는 서로의 능력이 발전하게 되고 결과적으로는 진짜 지폐와 위조 지폐를 구별할 수 없을 정도(구별할 확률 $p_d$=0.5)에 이른다는 것.

다시 말해 Generative model $G$는 우리가 갖고 있는 data $x$의 distribution을 알아내려고 노력한다. 만약 $G$가 정확히 data distribution을 모사할 수 있다면 거기서 뽑은 sample은 완벽히 data와 구별할 수 없다.

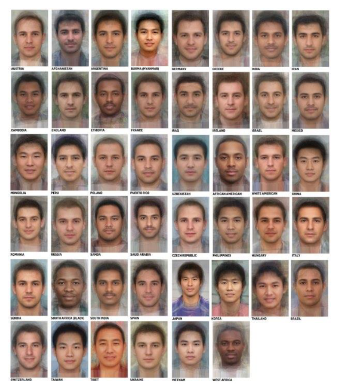
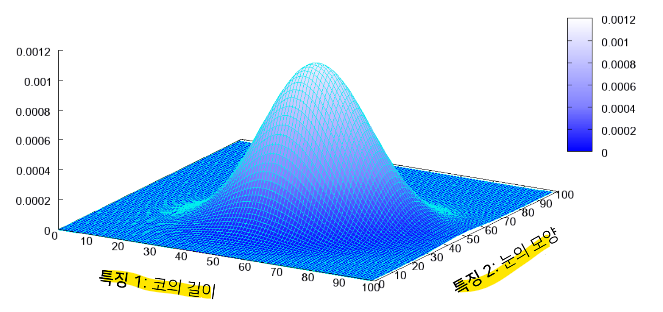
이런 이미지 데이터는 다차원 특징 공간의 한 점으로 표현이 된다.

얼굴 이미지도 통계적인 data distribution이 있고 이를 수치적으로도 표현 할 수 있다.

다양한 특징들이 각각 확률 변수가 되는 분포를 다변수 확률분포라 한다.

특징 1: 코의 길이
특징 2: 눈의 모양

한편 Discriminator model $D$는 현재 자기가 보고 있는 sample이 training data에서 온 것(진짜)인 지 혹은 $G$로부터 만들어진 것인 지를 구별하여 각각의 경우에 대한 확률을 Estimate한다.

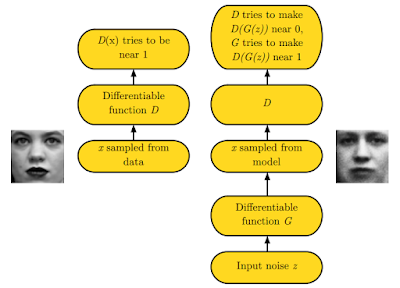
따라서 위 그림을 보면 $D$는 data로부터 뽑은 sample $x$는 $D(x) = 1$ 이 되고, $G$에 임의의 noise distribution으로부터 뽑은 input 값인 z를 넣고 만들어진 sample에 대해서는 $D(G(z))=0$ 가 되도록 훈련을 해야한다.

즉 $D$는 실수할 확률을 낮추는 것을 목표로 (min)
$G$는 $D$가 실수를 하도록(max)하는데, 이를 "minimax two-player game or minimax problem"이라고 한다.

$G$와 $D$는 꼭 Neural network로 만들 필요가 없다. 둘의 역할을 잘만 해주면 되기 때문이다.
근데 Neural network를 사용하면 많은 장점이 있기 때문에 사용하는 것 같다.

Adversarial Nets

Generator와 Discriminator와의 minimax 경쟁을 수식으로 표현해보자
수식은 Binary Cross-Entropy에서 영감을 얻어 사용한다. (확률이기 때문에)

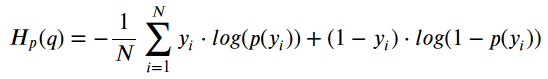
여기서 y는 실제 데이터일 때 1, 생성한 데이터일 때 0이고, p(y)는 실제 데이터일 확률을 의미한다. 그리고 이 값들의 Expectation의 합에 마이너스 부호가 붙게 된다.

일단 Generaots's distribution $P_g$ over data x를 학습하기 위해 generator의 input으로 들어갈 noise variables $P_z(z)$에 대한 prior를 정의하고, data space의 mapping을 $G(z;\theta_g)$라고 표현한다.

여기서 $G$는 미분 가능한 함수로써 $θ_g$를 parameter로 갖는 multilayer perceptron이다.

한편, Discriminator 역시 multilayer perceptron으로 $D(x;θ_d)$로 나타내며 output은 single scalar 값이 되겠다(0 or 1확률이므로). D(x)는 x가 $p_g$가 아닌 data distribution으로부터 왔을 확률을 나타낸다.

그래서 수식으로 정리하여 식이 완성 되는 것이다. (value function $V(G,D)$에 대해서 minimax probelm을 푸는 것과 같아진다.)

예시를 들어서 설명해 보겠다!

최댓값 최솟값

가장 이상적인 상황에서의 $D$는 아주 구별을 잘하는 녀석일 것이다.

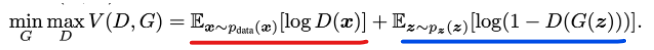
만약 $D$가 보는 Sample $x$가 실제로 data distribution(train 데이터)에서 온 것이라면, $D(x)=1$이다.
그러면 첫번째 term에서 log값이 사라진다.
$G(z)$가 만들어낸 녀석이라면 $D(G(z)) = 0$이므로 두 번째 term 역시 0으로 사라진다.
이 때가 D의 입장에서 V의 "최대값"을 얻을 수 있다는 것은 자명하다.

반대로 G의 입장에서 생각한 "최솟값"도 비슷하다.

• D가 구분을 못하는 경우 $D(G(z)) = 1$
• 진짜를 0, 가짜를 1로 뱉는경우가 "최소"
• log 안의 D값이 0이되어 V 값이 $-∞$로 간다.

GAN 학습 과정

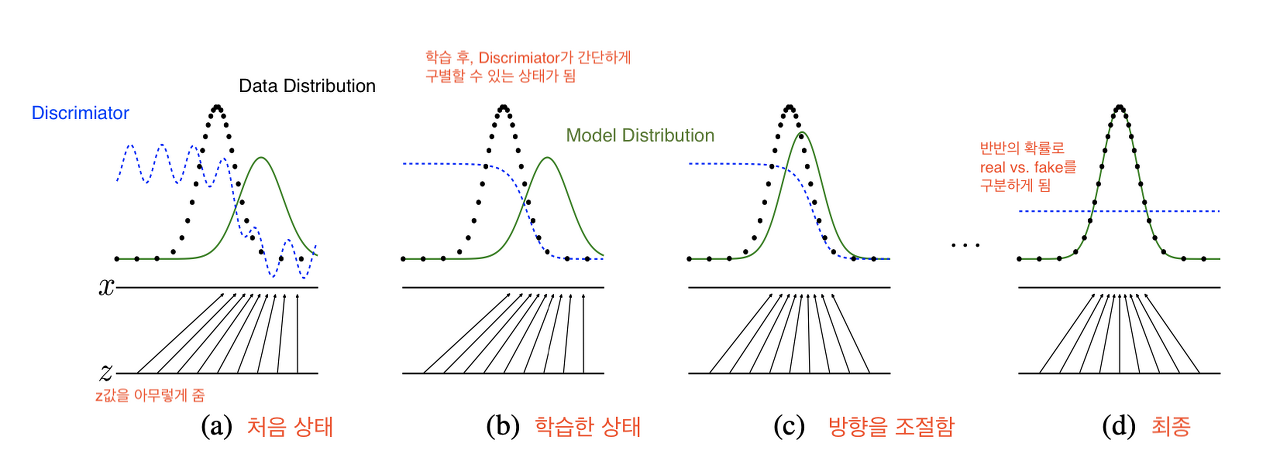
• 검은 점선이 data generating distribution (실제 데이터 분포)
• 파란 점선이 discriminator distribution (분류 분포)
  학습을 반복하다보면 가장 구분하기 어려운 구별 확률인 0.5 상태가 된다.
• 녹색 선이 generative distribution (가짜 데이터 분포)

밑에 $x$와 $z$선은 각각 $x$와 $z$의 domain을 나타내며, 위로 뻗은 화살표가 $x=G(z)$의 mapping을 보여준다.

처음 시작할 때는 (a)와 같이 $p_g$가 $p_\text{data}$와 전혀 다르게 생긴 것을 볼 수 있고 이 상태에서 discriminator가 두 distribution을 구별하기 위해 학습을 하면 (b)와 같이 smooth하고 잘 구별하는 distribution이 만들어진다.

이후 $G$가 현재 discriminator가 구별하기 어려운 방향으로 학습을 하면 (c)와 같이 좀 더 $p_g$가 $p_\text{data}$와 가까워지게 된다.

학습을 반복하다 보면 결국에는 $p_g = p_\text{data}$가 되어 $D$가 둘을 구분 못하는 $D(x) = 1/2$ 상태가 된다.

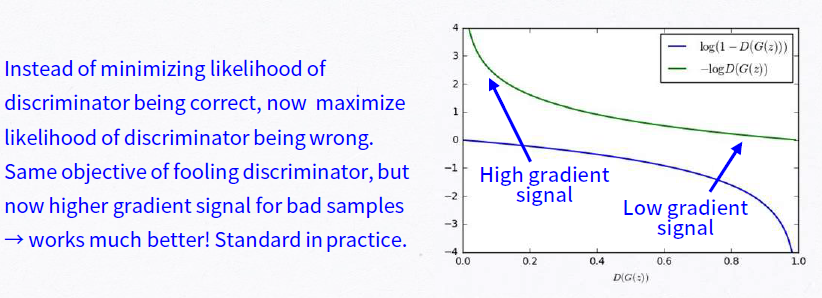
논문에서는 value finction에서 $\underset{G}{\text{minimize}}\; \mathbb{E}_{z \sim p(z)}\left[\log (1-D(G(z)))\right]$ 대신에 $\underset{G}{\text{maximize}}\; \mathbb{E}_{z \sim p(z)}\left[\log D(G(z))\right]$로 학습을 시킨다.

저자는 이론적인 동기로부터 수정을 한것이 아니라 순수하게 실용적인 측면에서 적용을 한 것이라 한다.
이유는 학습 초기에, $G$가 초기에는 아주 이상한 image들을 생성하기 때문에 $D$가 너무도 쉽게 이를 real image와 구별하게 되고 따라서 $log(1−D(G(z)))$ 값이 매우 saturate하여 gradient를 계산해보면 아주 작은 값이 나오기 때문에 학습이 엄청 느리다.

하지만 문제를 $\underset{G}{\text{maximize}}\; \mathbb{E}_{z \sim p(z)}\left[\log D(G(z))\right]$로 바꾸게 되면, 초기에 D가 G로 나온 image를 잘 구별한다고 해도 위와 같은 문제가 생기지 않기 때문에 원래 문제와 같은 fixed point를 얻게 되면서도 stronger gradient를 줄 수 있는 상당히 괜찮은 해결방법이다.

GAN 알고리즘

Theoretical Results

Minimax problem은 $P(x) = P(G)$ 에서 global optimum을 갖는다.

$G(z)$도 결국 x가 되므로 가치함수는 다음과 같이 전개할 수 있다.

(연속확률변수에 대한 기댓값은 $E[X] = \int xf(x)$로 계산 가능하다.)

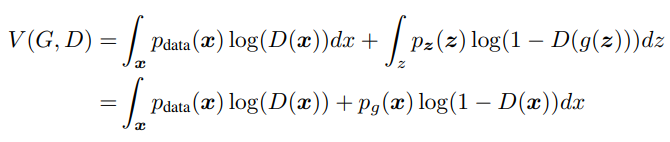
이때 $D(x)$를 y로 보게되면

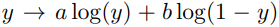
라는 식으로 전개 가능하고 미분해보면 $y = a/a+b$ 에서 maximum값을 얻는다. 즉, Generator가 고정된 상태에서 가장 Optimal한 Discriminator는

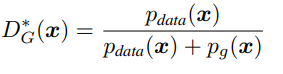
라는 값을 갖는다.

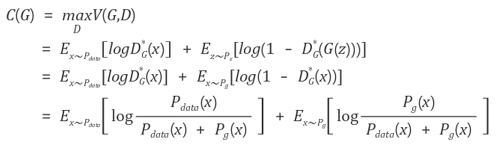
이제 생성기의 결과값에 대한 분포 $p_g$와 실제 훈련 자료의 분포 $p_\text{data}$ 간의 유사도를 비교하기 위해 젠슨-섀넌 발산(Jensen-Shannon Divergence)를 사용해 최적화 시켜주면 된다.

결국, $D$가 최적화되어있는 상황에서 $G$를 최적화시키는 일은
$JSD(p_\text{data}||P_g)$를 최소화 시키는 일과 같으며,이 것은 결국 $p_\text{data}$와$P_g$사이의 Jensen-Shannon Divergence를 최소화시키는 일로, Generated data의 distribution이 Real data의 distribution에 가까워지도록 하는 일이라는 뜻이 된다.
GAN은 실제 주어진 data와 동일한 형태의 distribution을 구해나가는 알고리즘이며, 우리는 이로써 GAN이 주어진 dataset의 distribution을 알아내는 알고리즘이라는 결론을 얻을 수 있다.

결과

노란색 박스가 Generator로 만들어진 이미지이다.

다음은 GAN을 구현해보는 글을 올리겠다..!