미시간대 강의_dropout

Weight Initialization

• 가중치의 초기값을 어떻게 설정해줘야 할까?
  
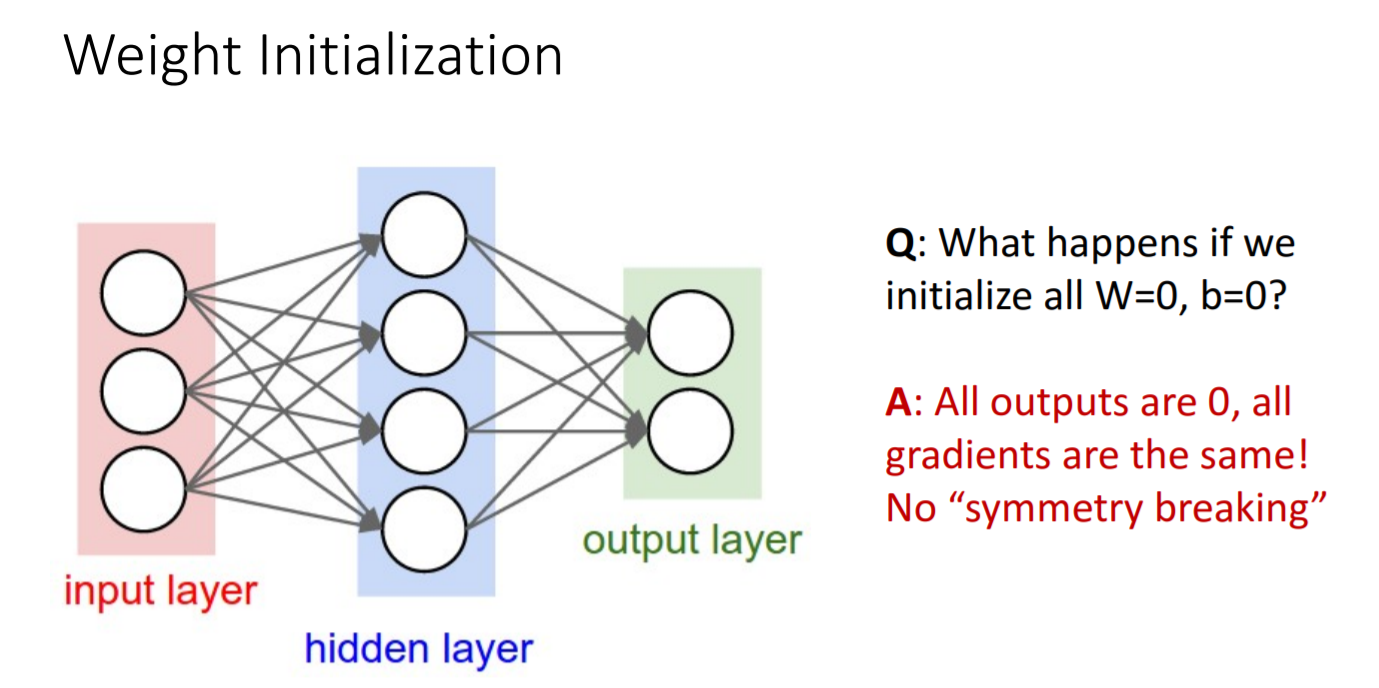
• 시도 1) 만약 초기값을 모두 0으로 설정한다면 모든 gradient의 값이 0이 될 것이므로 의미없는 훈련을 하게되는 셈이다.
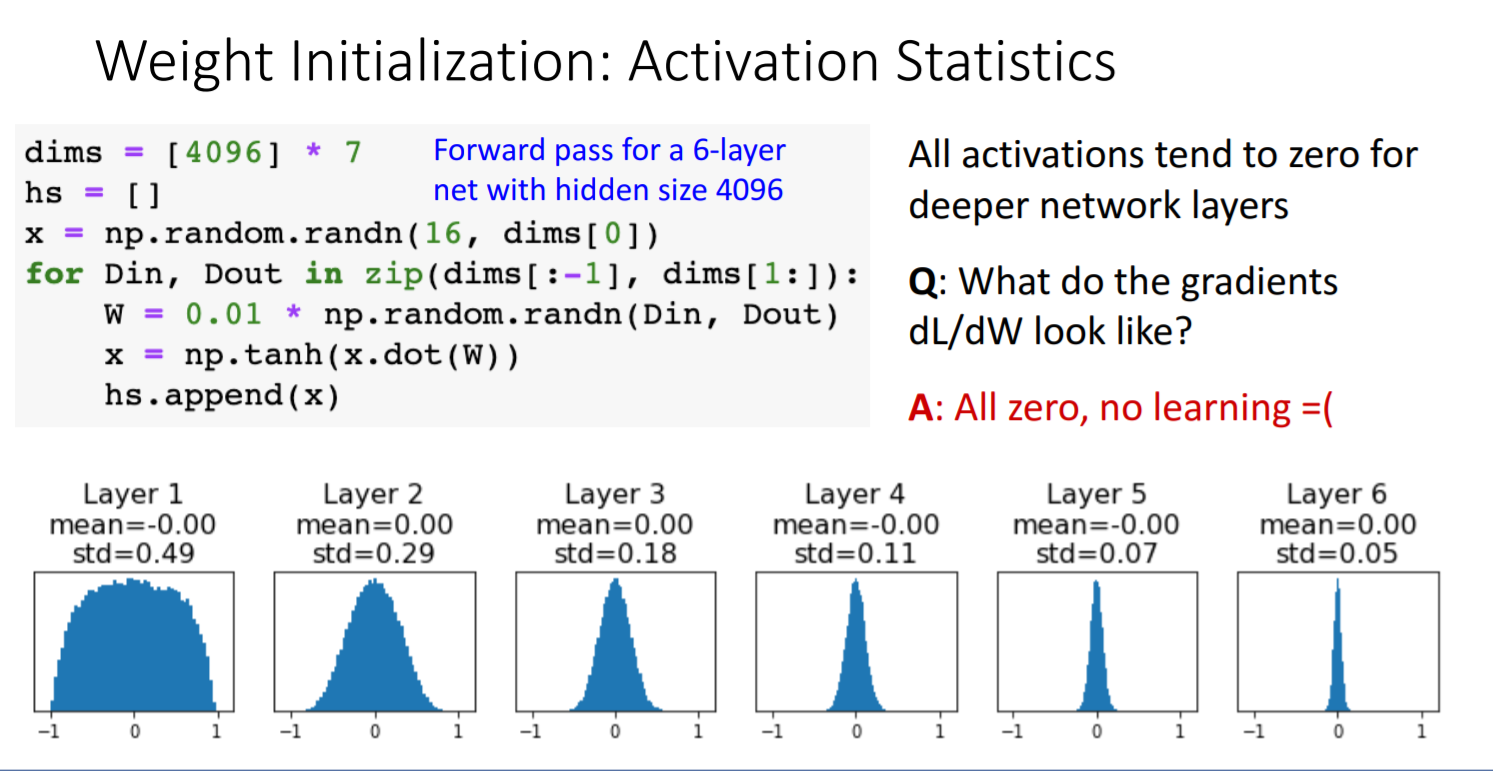
• 시도 2) 그러면 무작위의 작은 숫자로로 설정해보는 것은 어떨까?
  
• 6개의 layer만 통과해도 vanishing gradient문제가 발생한다.
  
• 시도 3) 해결방안으로 weight deviation을 0.01>0.05로 늘려줘볼까?
  
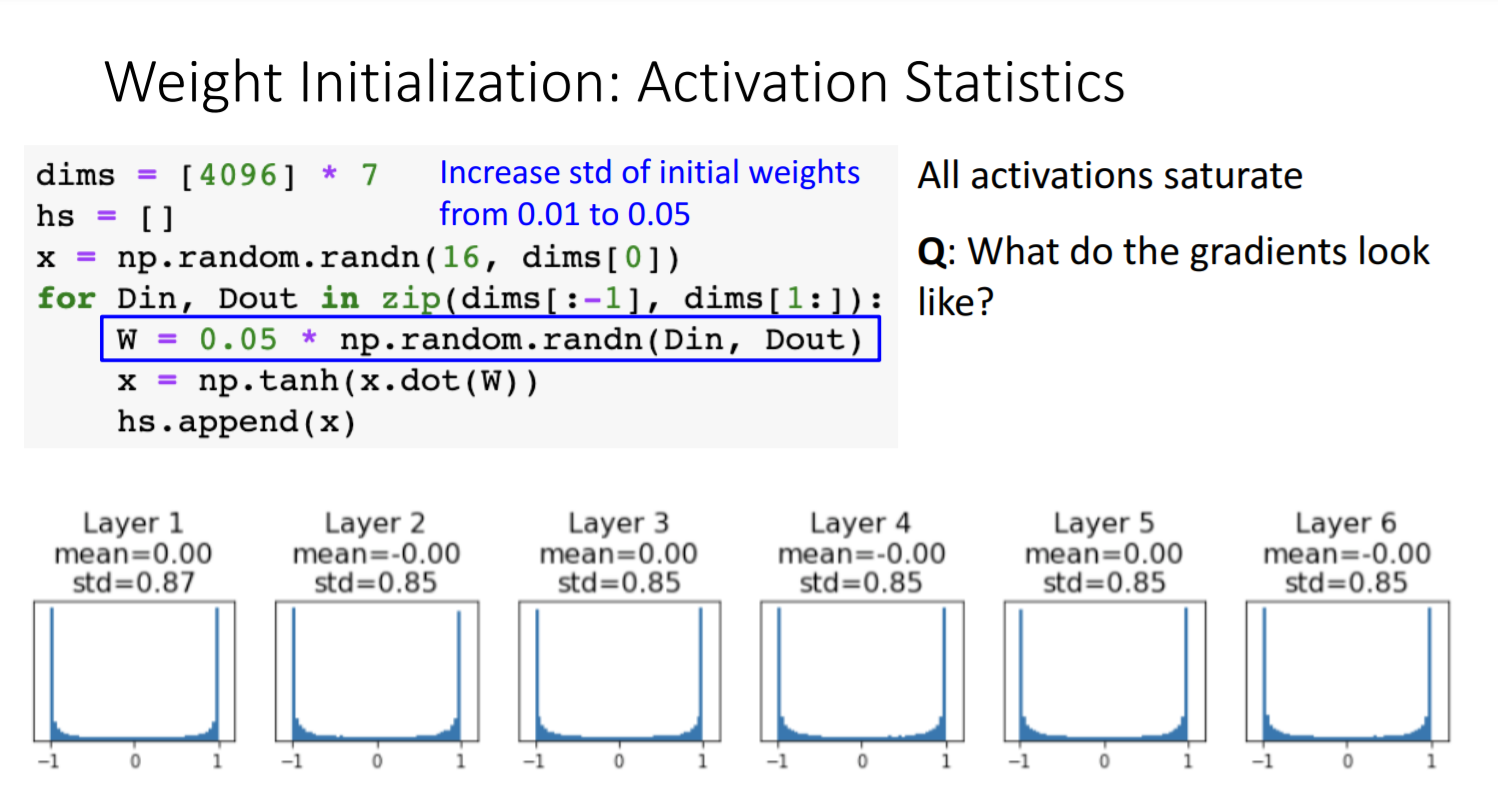
• saturation 문제가 발생한다.(tanh 통과하면서 값이 양 극단으로 감)
• weight value가 너무 커서도 너무 작아서도 안되는구나.
• 시도 4) Xavier Initialization - 활성화 함수: tanh
  
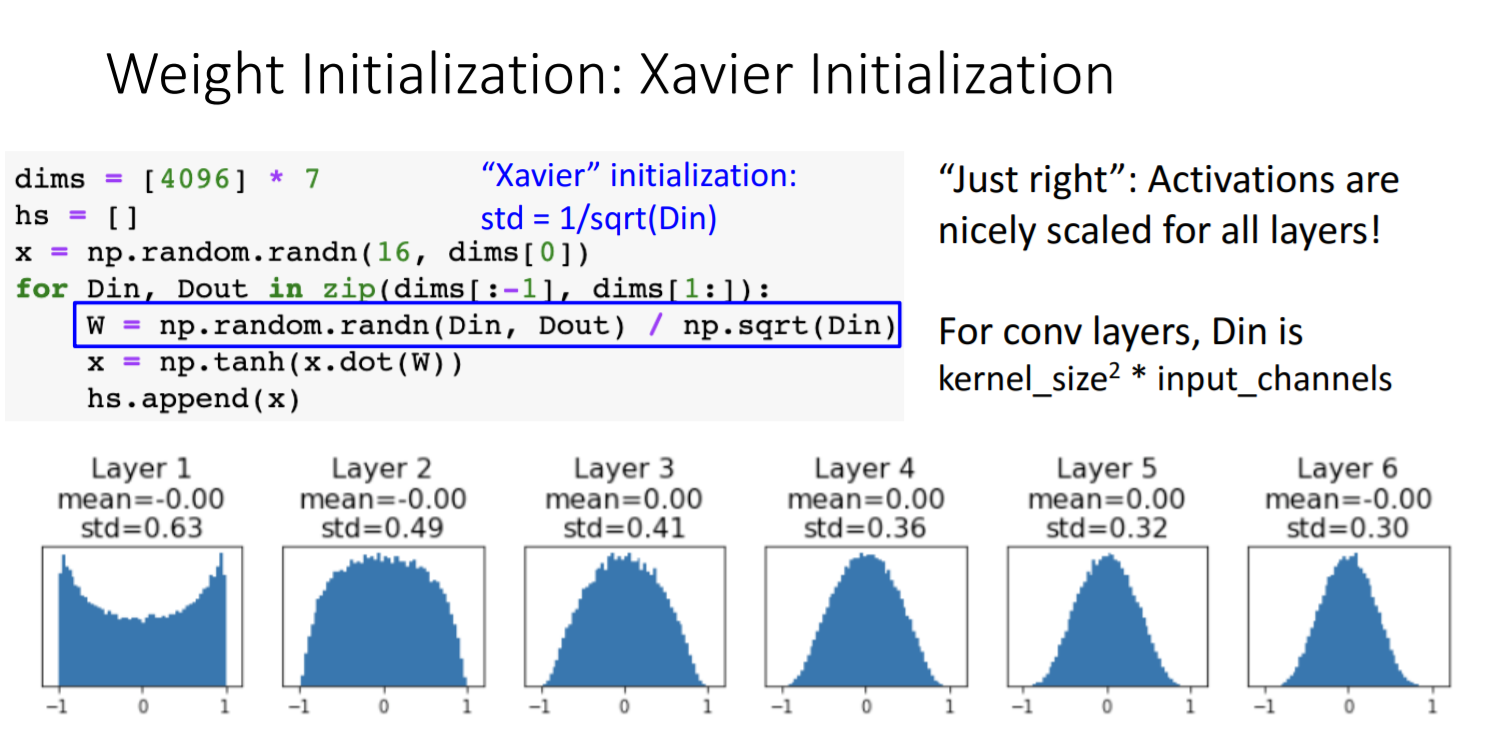
• 효과적!
  
• Xavier Initialization이란 입력과 출력의 분산을 똑같이 하는 것이다.
• 시도 5) Xavier Initialization - 활성화 함수: relu?
  
• 음수 값을 모두 없애므로 학습에 실패하고 있는 것을 확인할 수 있다.
• 그러면 활성화 함수로 relu로 쓸 수는 없는 걸까?
• 시도 6) Kaiming Initialization- 활성화 함수: relu
  
• 음수 부분이 사라졌으므로 분산을 두배로 scaling해준다.

Residual Network에서의 weight initialization

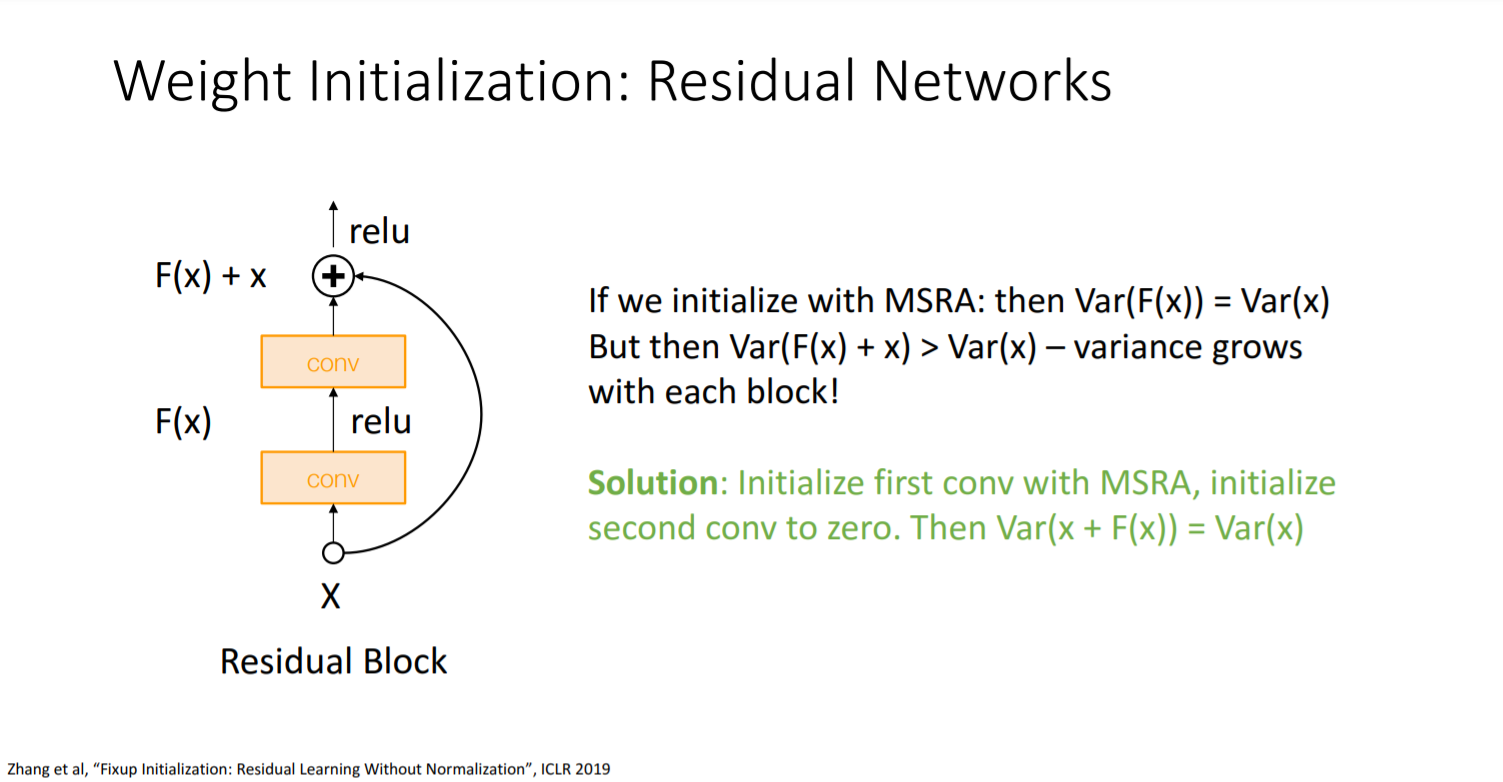
• 문제: residual network를 통과하게 된다면 분산이 계속 커지게 되는 문제가 발생한다.
• 해결방안: 처음 convolutional layer는 MSRA로 weight initialization 구현, 두번째 convolutional layer는 0으로 초기화를 한다.
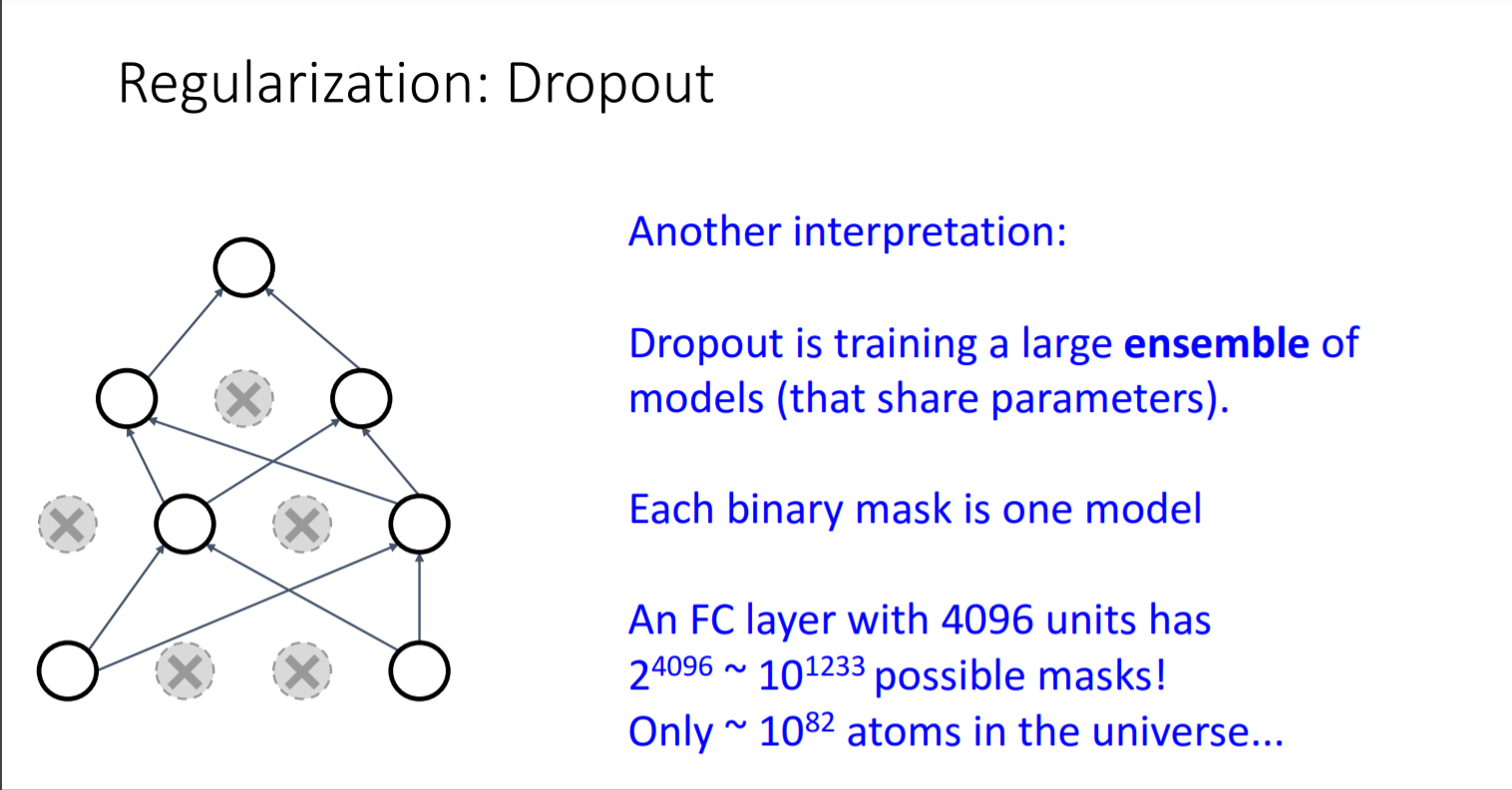
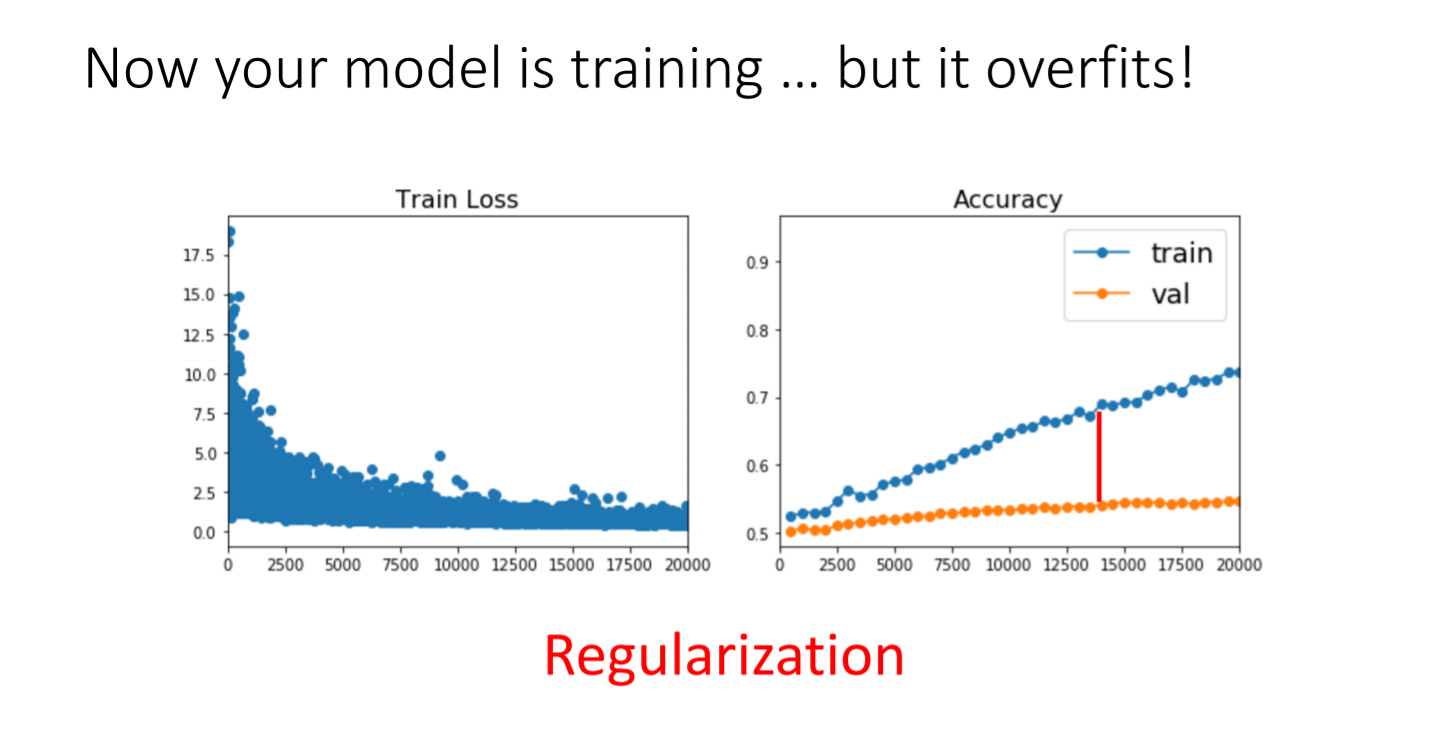
• Initialization을 잘 설정해줘서 gradient가 잘 나오더라도 overfitting문제가 발생한다. 이를 해결하기 위해 regularization을 도입해야한다. 전의 강의에서 L2 regularization에 대해 배웠는데 이번에는 regularization의 한 방법인 dropout에 대해 배워보겠다.
  

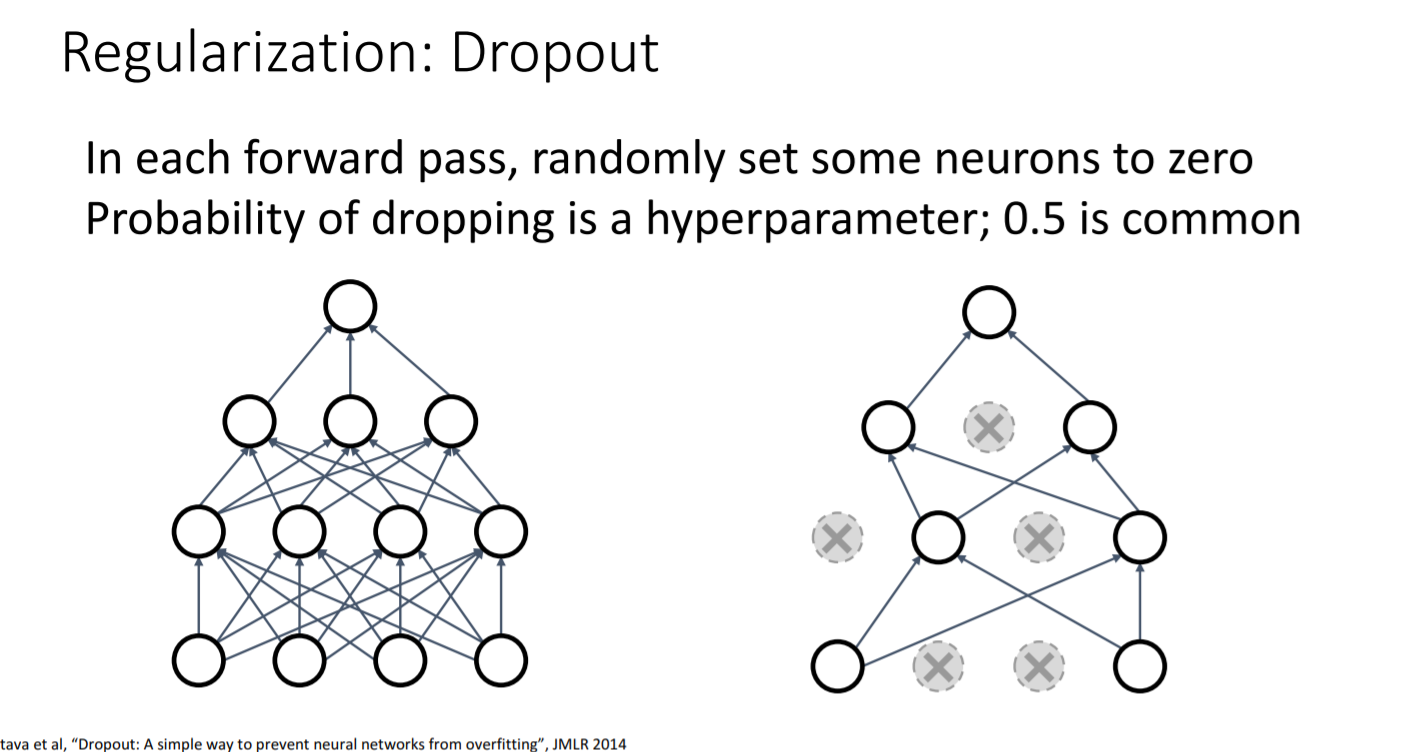
Dropout

• Dropout이란?
  forward pass에서 0.5의 확률로 뉴런이 작동하지 않도록 하는 것이다.
  
• 코드로 구현
  
• Dropout의 장점1
  더 견고하게 분류를 할 수 있다. 모든 특징들이 아니라 몇 가지 특징만으로도 제대로 분류 가능하도록 한다.
  
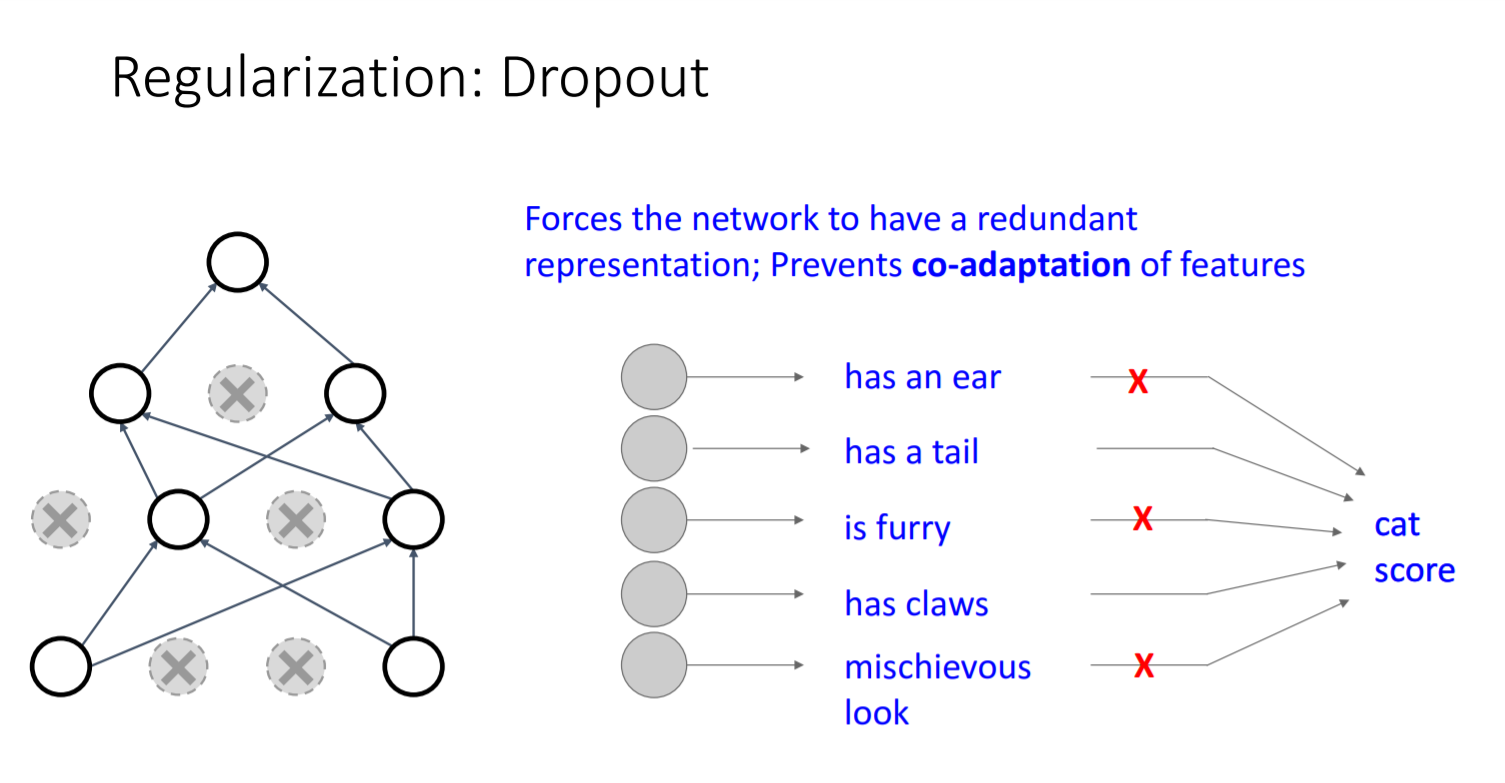
• Dropout의 장점2
  가중치를 공유하는 network의 부분집합인 subnetwork를 아주 많이 구할 수 있다. 그 subnetwork들의 ensemble들을 training하기 때문에 경우의 수가 많아져 성능이 올라갈 것으로 예상된다.