0. Preface

Time Series에서 $y_t$와 $y_{t+k}$사이의 관계를 관찰해보도록 하자. 여기서 이 간격 $k$를 lag라고 부른다.

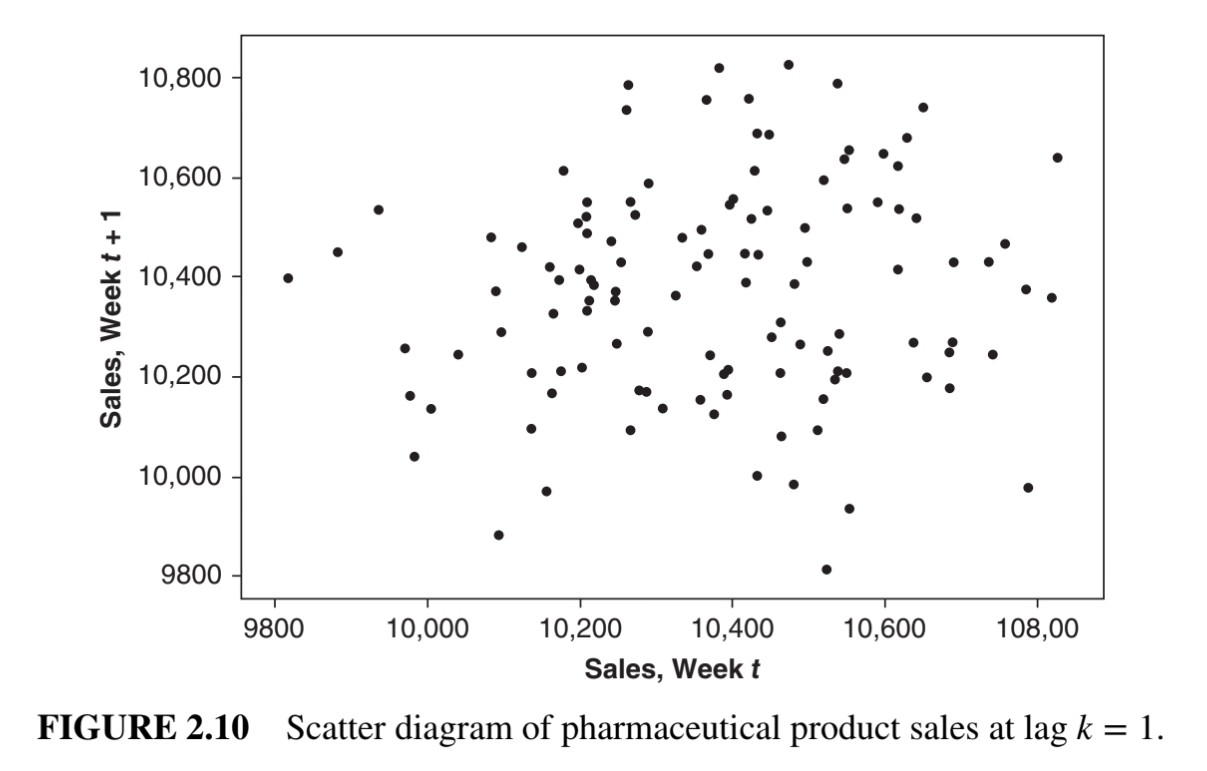
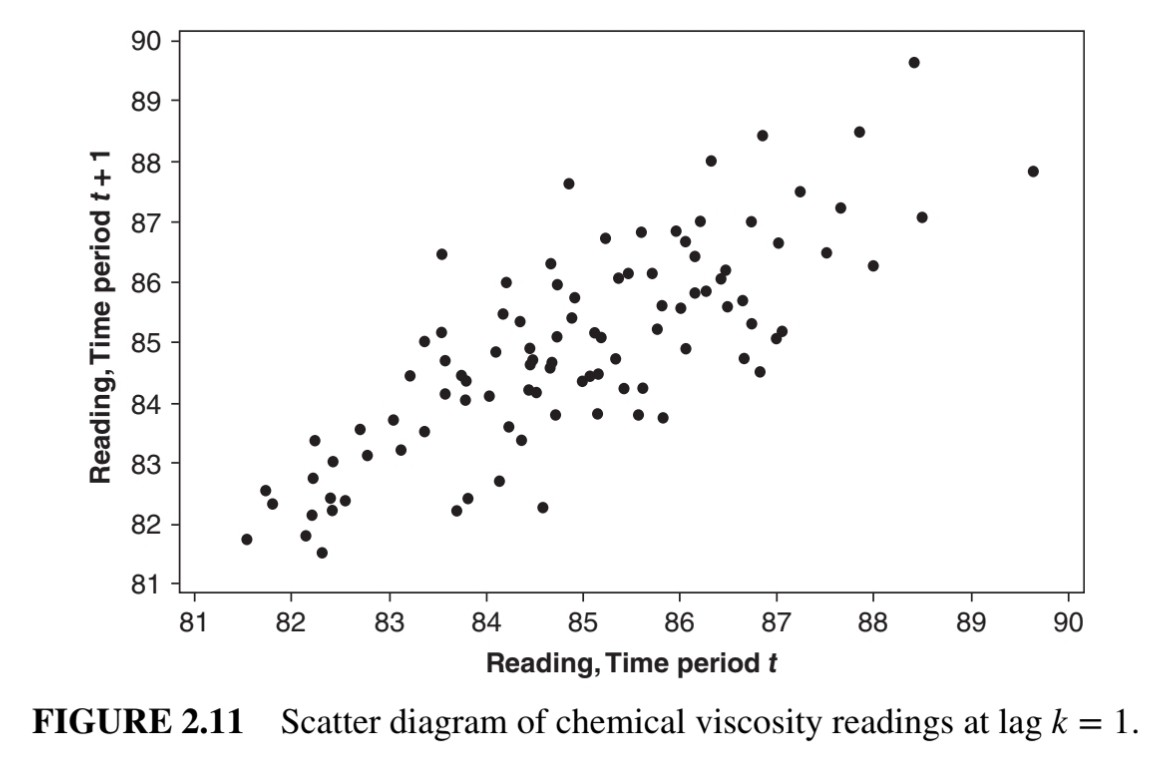
위 두 그림은 모두 lag가 1일 때의 scatter plot이다. 이때 figure 2.10은 데이터 간이 uncorrelated한 것으로 보이고, figure 2.11은 데이터 간이 positively correlated한 것으로 보인다.

이번 포스트에서는 이와같은 correlation을 설명하는 Autocovariance와 Autocorrelation을 알아보도록 한다.

1. Autocovariance

Autocovariance의 정의는 아래와 같다.

(일반적인 covariance가 서로 다른 두 확률변수를 parameter로 취하는 것과 달리 하나의 데이터셋 내에서 covariance를 구하는 것이기에 auto가 붙는 것같다.)

이때 $\gamma_k$를, $k$를 parameter로 취하는 하나의 함수로 볼 수 있다. 이를 Autocovariance Function이라고 부른다.

2. Autocorrelation Coefficient

공분산을 알아봤으니 상관계수도 알아보도록 하자. 정의는 아래와 같다.

autocovariance의 경우와 마찬가지로 $\rho_k$를, $k$를 parameter로 취하는 하나의 함수로 볼 수 있다. 이를 Autocorrelation Function(ACF)라고 부른다.

만약 $y_t$가 모든 $t$에서 동일한 분포를 따른다면 $\rho_t$를 아래와 같이 단순화할 수 있다.

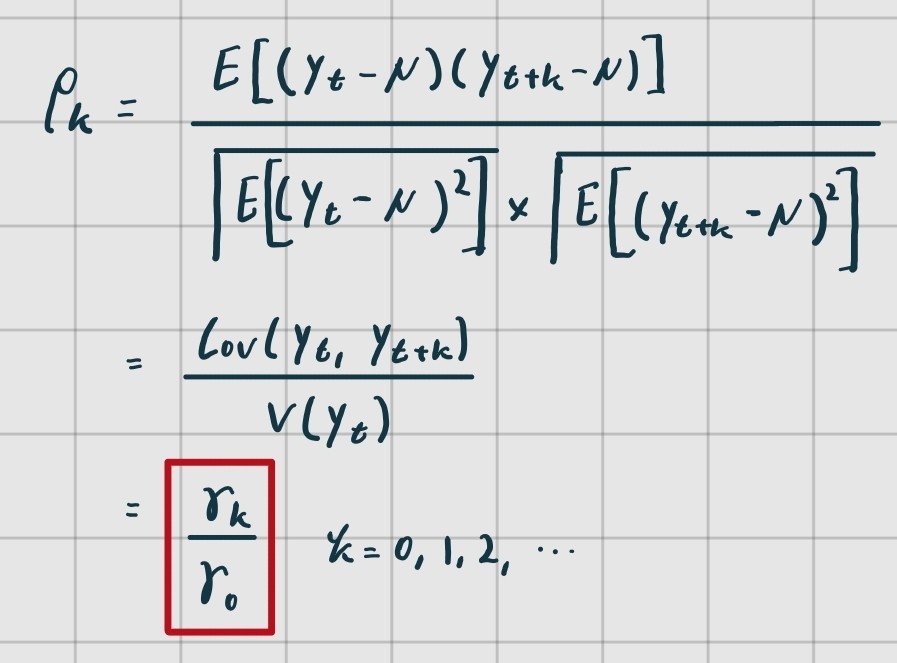
3. Some Sample Functions

위에서 언급한 autocovariance, autocorrelation coefficient는 모수, 즉 $\mu$를 알 때 값을 알 수 있었다. 모수를 모를 때 사용할 수 있는 sample estimators를 알아보자.

• 일반적으로, 최소한 50개의 observation을 사용해야 reliable한 sample ACF를 얻을 수 있다.

• sample ACF는 $k \leq T/4$인 $k$에 대해 계산하는 것이 바람직하다.

또한, sample ACF의 plot을 관찰하면 해당 데이터셋이 stationary한지 예측할 수 있다.

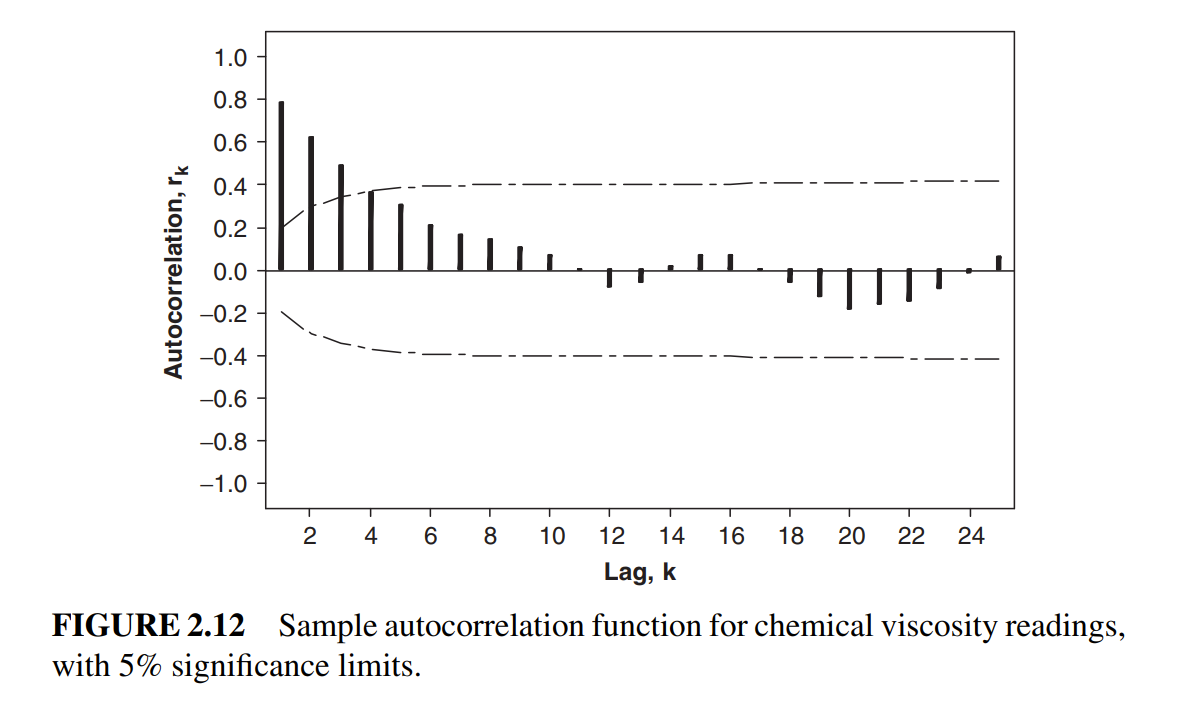
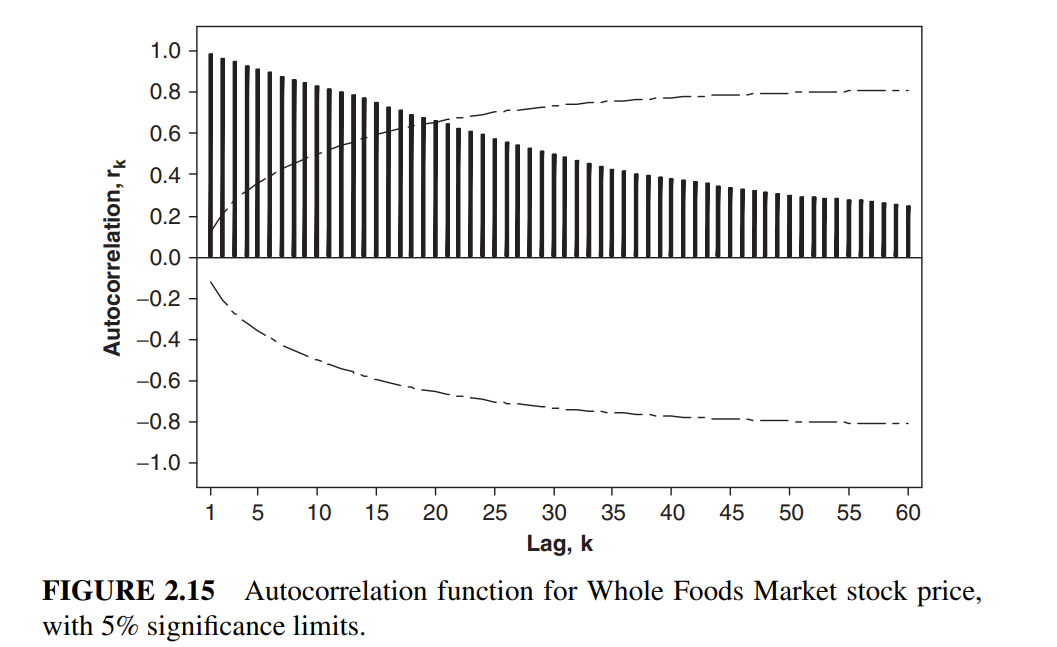
figure 2.12는 stationary한 데이터의 ACF plot이고, figure 2.15는 nonstationary한 데이터의 ACF plot이다. 2.12는 0 근처로 수렴하고, 2.15는 그렇지 않은 것을 확인할 수 있다.

일반적으로, 15~20 lag이내로 ACF가 0 근처로 수렴하지 않으면 nonstationary하다고 말할 수 있다.

---

Wonder 1... stationary하지 않을 때의 $r_k$는 어떻게 계산하는지 궁금. 직관적으로 생각하면, $c_k/(s_ts_{t+k})$가 아닐까싶다.

Reference: Introduction to Time Series Analysis and Forecasting 2nd by Douglas C. Montogomery

질문, 조언 환영합니당 ■