Strictly Stationary Time Series

Time Series 중에서도 Stationary Time Series는 중요한 타입이다. 이 게시물에서는 그 중에서도 Strictly Stationary Time Series를 다루도록한다(Stationary Time Series의 분류에는 Weakly Stationary Time Series도 존재한다).

정의는 다음과 같다.

A time series is said to be Strictly Stationary if its properties are not affected by a change in the time origin.

풀어서 설명하면, 만약 joint prob. dist'n of the observations $y_t, y_{t+1}, ... , y_{t+n}$이 $y_{t+k}, y_{t+k+1}, ... , y_{t+k+n}$의 joint prob. dist'n과 같다면 그 time series가 strictly stationary하다고 말할 수 있다.

n = 0일 때 위의 말이 성립한다면, 모든 $t$에서 $y_t$가 동일한 확률분포 $f(y)$를 따르게된다.

아래 plot은 모든 $t$에서 동일하게 $f(y)$를 따르는 한 예시 plot이다. 분포를 분홍색 펜으로 표현해보았다.

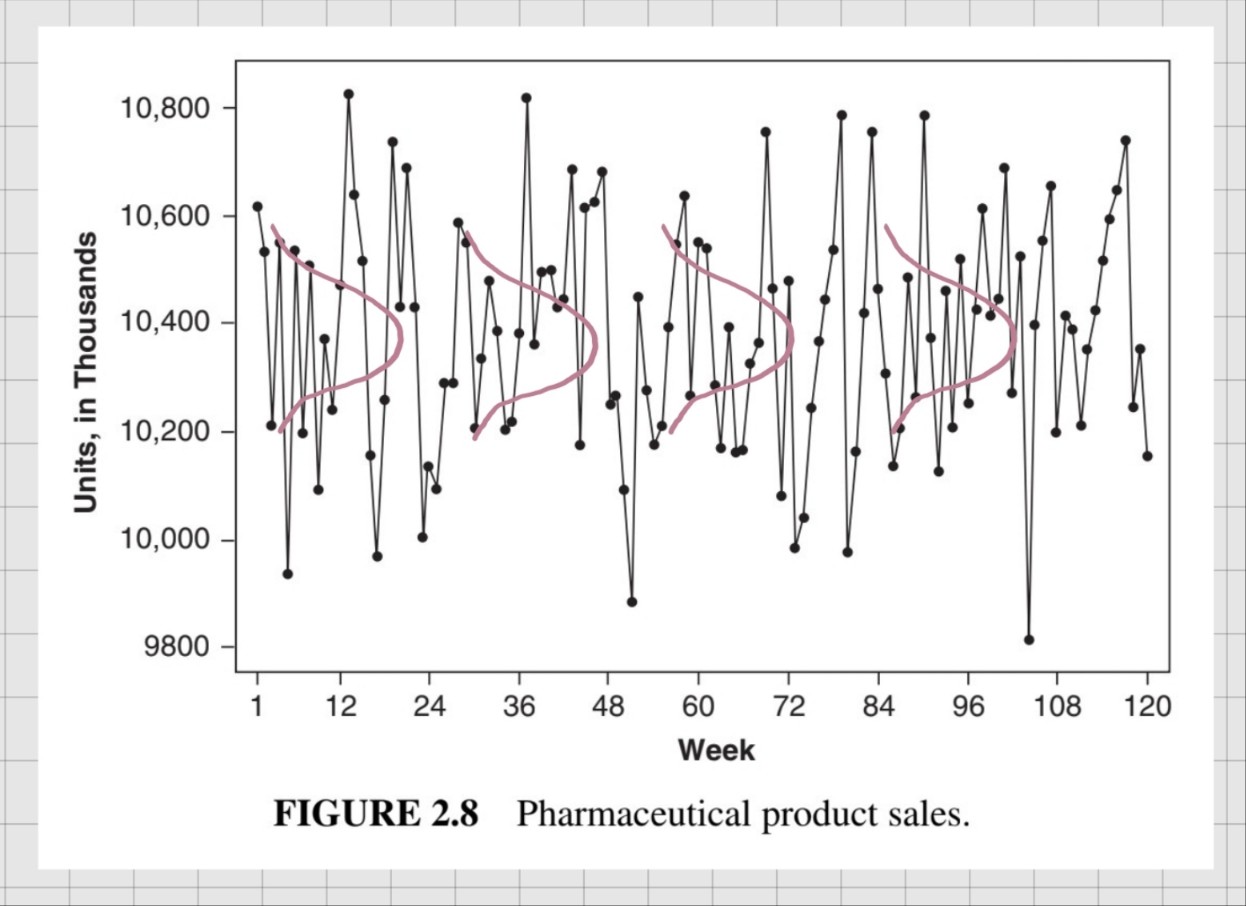
모두 동일한 분포를 따를 때의 몇 가지 summary statistics는 아래와 같다.

sample variance를 구할 때 $T-1$이 아니라 $T$로 나눈 점이 특이한데, 보통 시계열분석에서는 $T$가 충분히 크기때문에 그냥 $T$로 나눈다고한다.

---

• 시계열 분석에서는 확률변수의 대문자 구분을 그리 신경쓰지 않는듯하다. 당장 위의 constant mean만 봐도... 원래같았으면 $E(Y)$가 맞기 때문이다.

Reference: Introduction to Time Series Analysis and Forecasting 2nd by Douglas C. Montogomery

질문, 조언 환영합니당 ■