Ch4. Classification

조성호·2025년 8월 5일
ClassificationISLPmachine learning

An Introduction to Statistical Learning

목록 보기
2/2
post-thumbnail

1. Stock Market Data

Stock market data는 2001년부터 2005년까지 S&P500 지수의 변동을 보여주는 데이터이다.

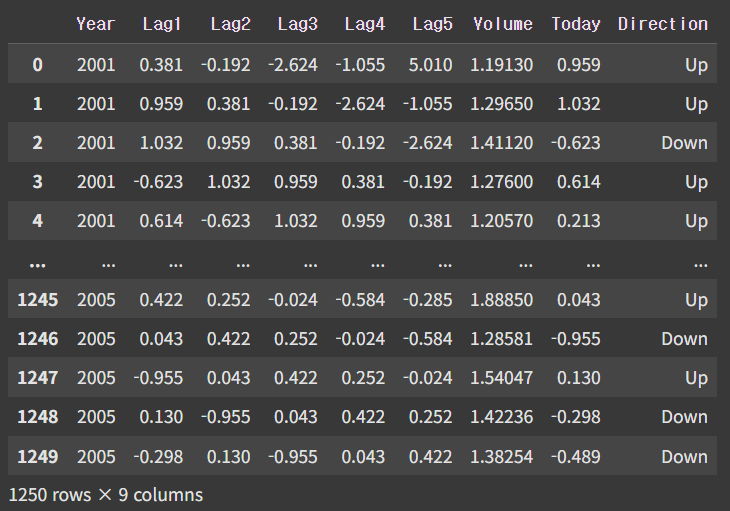
Today는 당일의 수익률을 나타내며, Lag1은 전날의 수익률을 나타내고 Lag2는 전전날의 수익률을 나타낸다. Lag3, 4, 5도 마찬가지이다. Direction은 오늘 시장이 올랐는가, 내려갔는가를 나타낸다. Today가 양수라면 Direction은 Up, 음수라면 Direction은 Down이다. Volume은 당일 거래량(10억 주 단위)를 나타낸다.

먼저 필요한 모듈을 설치하고 import한다.

# 코랩에서 구동
%%capture
!pip install ISLP
# 코랩에서 구동
%%capture
import numpy as np
import pandas as pd
from matplotlib.pyplot import subplots
import statsmodels.api as sm
from ISLP import load_data
from ISLP.models import (ModelSpec as MS, summarize)
from ISLP import confusion_table
from ISLP.models import contrast
from sklearn.discriminant_analysis import (LinearDiscriminantAnalysis as LDA, QuadraticDiscriminantAnalysis as QDA)
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression

데이터를 로드하고, 상관관계와 Volume의 그래프를 그려본다.

Smarket = load_data("Smarket")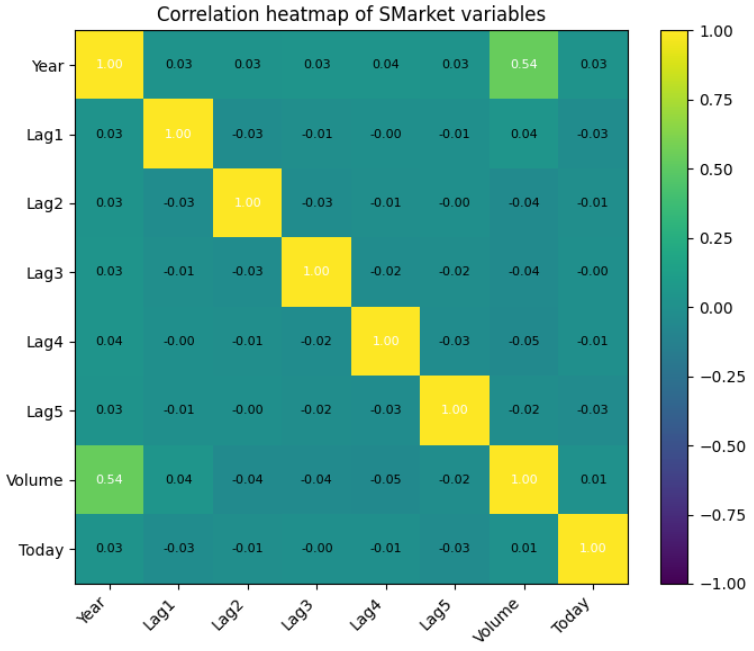

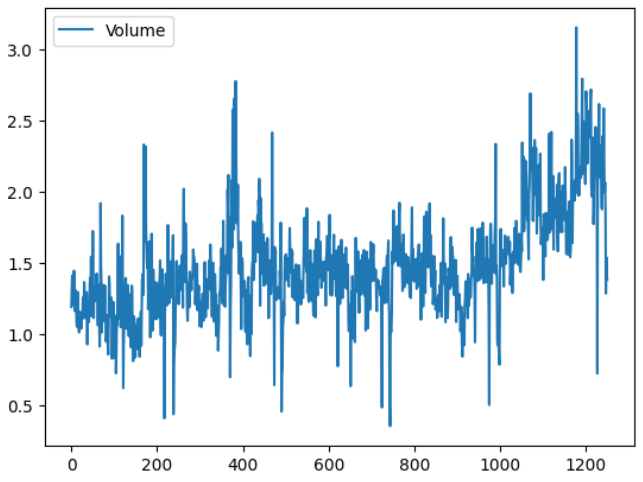
상관관계는 Voulume과 Year 간에 양의 상관관계가 존재하며, Volume은 시간이 지날수록 증가하는 양상을 보인다.

1.1. Logistic Regression

Lag와 Volume을 predictor로 하여 Direction을 분류해보자. 

allvars = Smarket.columns.drop(["Year", "Today", "Direction"])
design = MS(allvars)
X = design.fit_transform(Smarket)
y = Smarket.Direction == "Up"
glm = sm.GLM(y, X, family=sm.families.Binomial())
results = glm.fit()
summarize(results)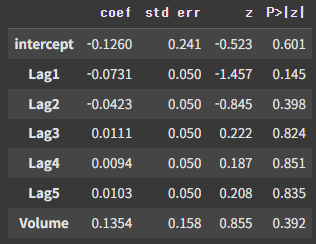

결과는 위와 같다. 그나마 Lag1이 가장 p값이 작지만, 그마저도 약 0.15이기에 큰 수치이다.

이제 예측 결과를 확률로 변환하여 confusion table을 만들어보도록 하자. 0.5를 threshold로 삼아 0.5 보다 크면 Up, 그렇지 않으면 Down이 되도록 세팅한다. 또한 accuracy도 출력한다. 

probs = results.predict()
labels = np.array(["Down"]*1250)
labels[probs > 0.5] = "Up"
confusion_table(labels, Smarket.Direction)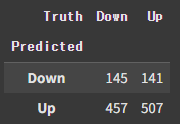

np.mean(labels == Smarket.Direction)

### np.float64(0.5216)

하지만 이 accuracy는 train test split을 하기 이전의 결과이기에, 그다지 신뢰할만하지 못하다. Split을 진행하고 다시 계산해보도록 하자. Train set은 2005년 이전의 데이터로 하고, test set은 2005년의 데이터로 한다. 

train = (Smarket.Year < 2005)
Smarket_train = Smarket.loc[train]
Smarket_test = Smarket.loc[~train]
Smarket_test.shape

### (252, 9)
X_train, X_test = X.loc[train], X.loc[~train]
y_train, y_test = y.loc[train], y.loc[~train]
glm_train = sm.GLM(y_train, X_train, family=sm.families.Binomial())
results = glm_train.fit()
probs = results.predict(exog=X_test)

D = Smarket.Direction
L_train, L_test = D.loc[train], D.loc[~train]
labels = np.array(["Down"]*252)
labels[probs>0.5] = "Up"
confusion_table(labels, L_test)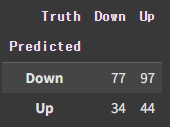

np.round(np.mean(labels==L_test), 3), np.round(np.mean(labels!=L_test), 3)

### (np.float64(0.48), np.float64(0.52))

Accuracy가 약 0.48로, 무작위 추측의 확률인 0.5보다 낮다.

Summarize 표에서 p값이 그나마 높았던 Lag1과 Lag2만 사용하여 예측을 진행해보자. 

model = MS(["Lag1","Lag2"]).fit(Smarket)
X = model.transform(Smarket)
y = Smarket.Direction == "Up"
X_train, X_test = X.loc[train], X.loc[~train]
y_train, y_test = y.loc[train], y.loc[~train]
glm_train = sm.GLM(y_train, X_train, family=sm.families.Binomial())

results = glm_train.fit()
probs = results.predict(exog=X_test)
labels = np.array(["Down"]*252)
labels[probs>0.5] = "Up"
D = Smarket.Direction
L_train, L_test = D.loc[train], D.loc[~train]
confusion_table(labels, L_test)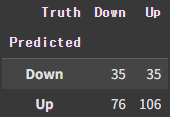

np.round(np.mean(labels==L_test), 3), np.round(np.mean(labels!=L_test), 3)

### (np.float64(0.56), np.float64(0.44))

Accuracy가 0.56으로, 모든 변수를 사용했을 때보다 상당히 값이 증가했다.

1.2. Linear Discriminant Analysis

Linear Discriminant Analysis(선형 판별 분석)을 사용하여 분류를 해보자. 이때 intercept는 제외하고 분석을 진행한다.

Smarket = load_data("Smarket")

model = MS(["Lag1","Lag2"]).fit(Smarket)
X = model.transform(Smarket)
train = (Smarket.Year < 2005)
X_train, X_test = X.loc[train], X.loc[~train]
D = Smarket.Direction
L_train, L_test = D.loc[train], D.loc[~train]

lda = LDA(store_covariance=True)
X_train, X_test = [M.drop(columns=["intercept"]) for M in [X_train, X_test]]
lda.fit(X_train, L_train)
np.round(lda.means_, 3)

### array([[ 0.043,  0.034],
###        [-0.04 , -0.031]])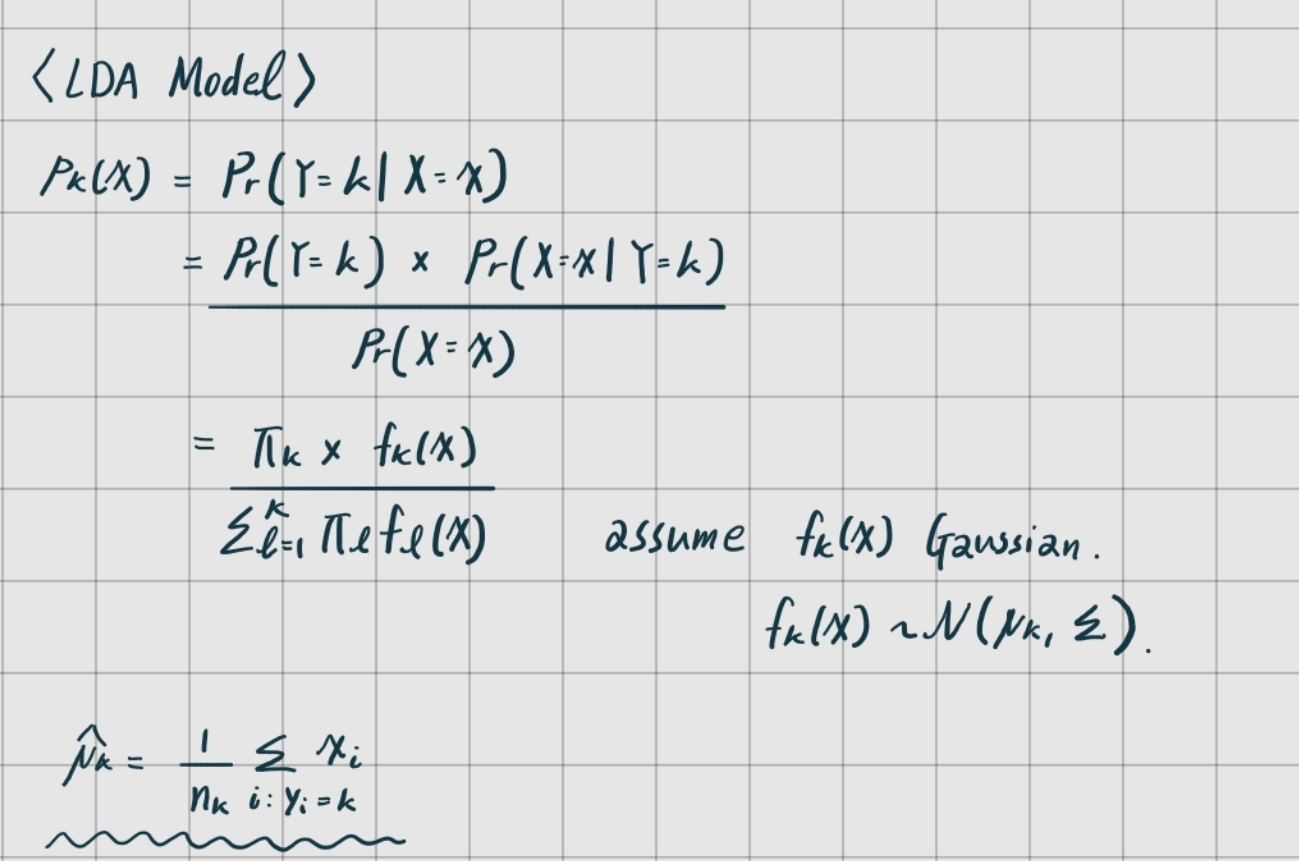

lda.means_는 추정된 μk^\hat{\mu_k}를 나타낸다.
즉 μ0^=[0.0430.034]\hat{\mu_0} = \begin{bmatrix} 0.043 \\ 0.034\end{bmatrix}, μ1^=[−0.04−0.031]\hat{\mu_1} = \begin{bmatrix} -0.04 \\ -0.031\end{bmatrix}이며 오늘의 장이 하락하는 장이었다면 평균적으로 이전 날과 전전 날의 장은 상승하는 장이었고, 오늘의 장이 상승하는 장이었다면 평균적으로 이전 날과 전전 날의 장은 하락하는 장이었다.

Confusion table을 통해 logistic regression의 경우와 비교해보자. 

lda_pred = lda.predict(X_test)
confusion_table(lda_pred, L_test)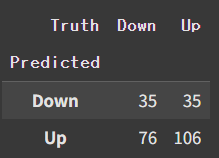

np.round(np.mean(lda_pred==L_test), 3), np.round(np.mean(lda_pred!=L_test), 3)

### (np.float64(0.56), np.float64(0.44))

Accurracy가 0.56으로, 로지스틱 회귀의 경우와 같다. Confusion table도 똑같다.

1.3. Quadratic Discriminant Analysis

Quadratic Discriminant Analysis(이차 판별 분석)을 사용하여 분류를 해보자. 이때 intercept는 제외하고 분석을 진행한다.

Smarket = load_data("Smarket")

model = MS(["Lag1","Lag2"]).fit(Smarket)
X = model.transform(Smarket)
train = (Smarket.Year < 2005)
X_train, X_test = X.loc[train], X.loc[~train]
D = Smarket.Direction
L_train, L_test = D.loc[train], D.loc[~train]

qda = QDA(store_covariance=True)
X_train, X_test = [M.drop(columns=["intercept"]) for M in [X_train, X_test]]
qda.fit(X_train, L_train)
qda_pred = qda.predict(X_test)
confusion_table(qda_pred, L_test)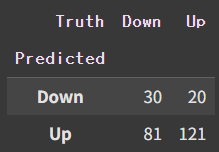

np.round(np.mean(qda_pred==L_test), 3), np.round(np.mean(qda_pred!=L_test), 3)

### (np.float64(0.599), np.float64(0.401))

약 0.6의 accuracy가 도출되었다. 주식시장에서 0.6의 예측 정확도는 꽤 높은 수치이다. 책에서도 "This level of accuracy is quite impressive for stock market data"라고 언급되어있다. 이는 앞선 linear한 모델보다 quadratic 모델이 true relationship을 더 잘 capture한다고 생각할 수 있게 한다.

1.4. Naive Bayes

다음은 Naive Bayes를 통해 분류를 진행해보도록 하자. GaussianNB를 사용할 것이다. 

Smarket = load_data("Smarket")

model = MS(["Lag1","Lag2"]).fit(Smarket)
X = model.transform(Smarket)
train = (Smarket.Year < 2005)
X_train, X_test = X.loc[train], X.loc[~train]
D = Smarket.Direction
L_train, L_test = D.loc[train], D.loc[~train]

NB = GaussianNB()
X_train, X_test = [M.drop(columns=["intercept"]) for M in [X_train, X_test]]
NB.fit(X_train, L_train)
nb_labels = NB.predict(X_test)
confusion_table(nb_labels, L_test)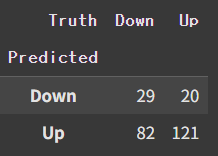

np.round(np.mean(nb_labels==L_test), 3), np.round(np.mean(nb_labels!=L_test), 3)

### (np.float64(0.595), np.float64(0.405))

Accuracy가 0.595로, QDA의 0.599보다 근소하게 떨어진다.

1.4 K-Nearest Neighbors

다음은 KNN을 이용해 분류를 해보겠다. 일단 K=1로 설정한 뒤 분류해보자. 

Smarket = load_data("Smarket")

model = MS(["Lag1","Lag2"]).fit(Smarket)
X = model.transform(Smarket)
train = (Smarket.Year < 2005)
X_train, X_test = X.loc[train], X.loc[~train]
D = Smarket.Direction
L_train, L_test = D.loc[train], D.loc[~train]

knn1 = KNeighborsClassifier(n_neighbors=1)
X_train, X_test = [M.drop(columns=["intercept"]) for M in [X_train, X_test]]
knn1.fit(X_train, L_train)
knn1_pred = knn1.predict(X_test)
confusion_table(knn1_pred, L_test)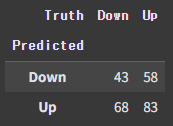

np.round(np.mean(knn1_pred==L_test), 3), np.round(np.mean(knn1_pred!=L_test), 3)

### (np.float64(0.5), np.float64(0.5))

약 0.5로, random guessing과 다르지 않은 수치가 나왔다. 왜 그런 것일까? 책에서도 나와있듯이 결정 경계가 "over-flexible"하기 때문이다. 경계가 일정한 line이 되지 않고 들쭉날쭉하여 over-fitting되었기 때문이다.

K=3으로 세팅한 후 다시 한 번 분류를 진행해보자.

knn3 = KNeighborsClassifier(n_neighbors=3)
knn3.fit(X_train, L_train)

knn3_pred = knn3.predict(X_test)
confusion_table(knn3_pred, L_test)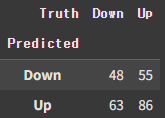

np.round(np.mean(knn3_pred==L_test), 3), np.round(np.mean(knn3_pred!=L_test), 3)

### (np.float64(0.532), np.float64(0.468))

Accuracy가 조금은 나아졌다. 그럼에도 QDA의 경우보단 낮은 수치이다.

2. Bikeshare Data

다음은 Bikeshare Data를 사용해 분류를 진행해보자.

Bike = load_data("Bikeshare")
Bike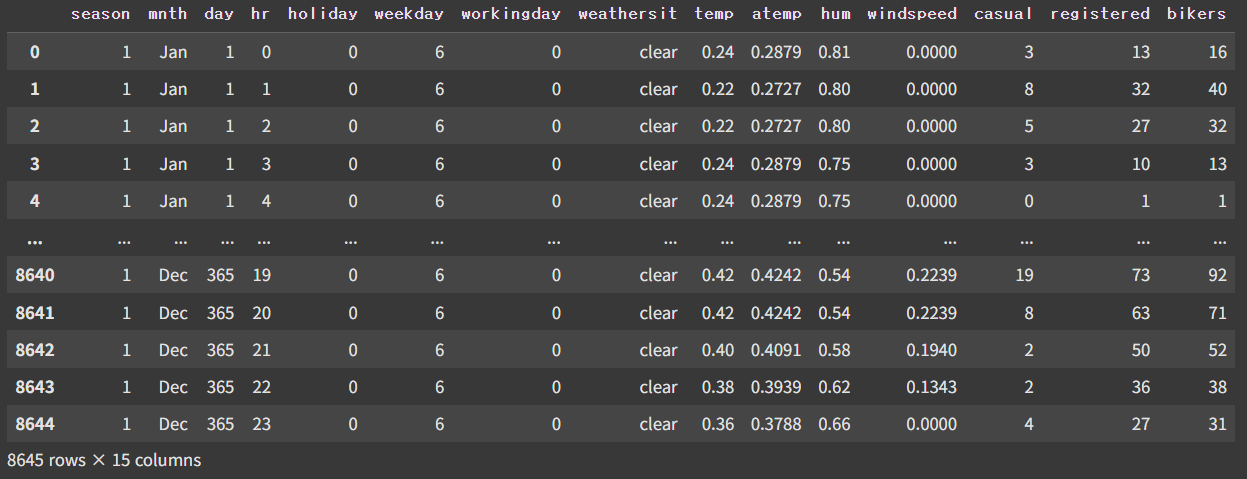

Bikeshare 데이터는 워싱턴 D.C.에서 진행한 자전거 대여 프로그램의 진행 로그이다. Target variable인 bikers는 해당 시간 에 대여된 자전거의 개수이다. 이전의 경우와 달리 타겟이 바이너리하지 않고, non-negative integer variable이라는 점에서 차이가 있다.

2.1. Linear Regression

hr_encode = contrast("hr", "sum")
math_encode = contrast("mnth", "sum")

X2 = MS([math_encode,
         hr_encode,
         "workingday",
         "temp",
         "weathersit"]).fit_transform(Bike)
Y = Bike["bikers"]
M2_lm = sm.OLS(Y, X2).fit()
summarize(M2_lm).head(15)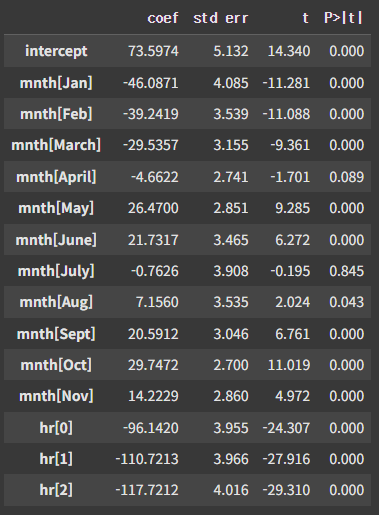

hr, mnth 변수에 대해서는 일반적인 Dummy Coding 대신 Effect Coding으로 처리했다. Effect coding의 주요한 특징은 다음과 같다.

  • 마지막 변수, 예를 들어 mnth[Dec]의 계수는 0이 아니다. 다른 모든 달의 계수를 합친 것의 음수값이다.
  • 각 계수는 평균으로부터의 차이로 해석할 수 있다. 예를 들어 January의 경우, 계수 -46.0871은 다른 모든 변수를 고정했을 때, 46.0871건의 대여가 연평균에 비해 적게 발생한다고 해석할 수 있다.

하지만 선형회귀를 사용할 경우 fitted value가 음수, 혹은 non-integer가 될 수 있기에 현재 Bikeshare 데이터에 사용하기에는 적합하지 않다.

2.2 Poisson Regression

포아송회귀모델을 사용해 분류를 진행해보자. 

Bike = load_data("Bikeshare")

hr_encode = contrast("hr", "sum")
math_encode = contrast("mnth", "sum")

X2 = MS([math_encode,
         hr_encode,
         "workingday",
         "temp",
         "weathersit"]).fit_transform(Bike)
Y = Bike["bikers"]

M_pois = sm.GLM(Y, X2, family=sm.families.Poisson()).fit()

선형회귀와 포아송회귀의 적합값을 비교해보자. 

fig, ax = subplots(figsize=(8,8))
ax.scatter(M2_lm.fittedvalues,
           M_pois.fittedvalues,
           s=20)
ax.set_xlabel("Linear Regression Fit", fontsize=20)
ax.set_ylabel("Poisson Regression Fit", fontsize=20)
ax.axline([0,0], c="black", linewidth=3,
          linestyle="--", slope=1)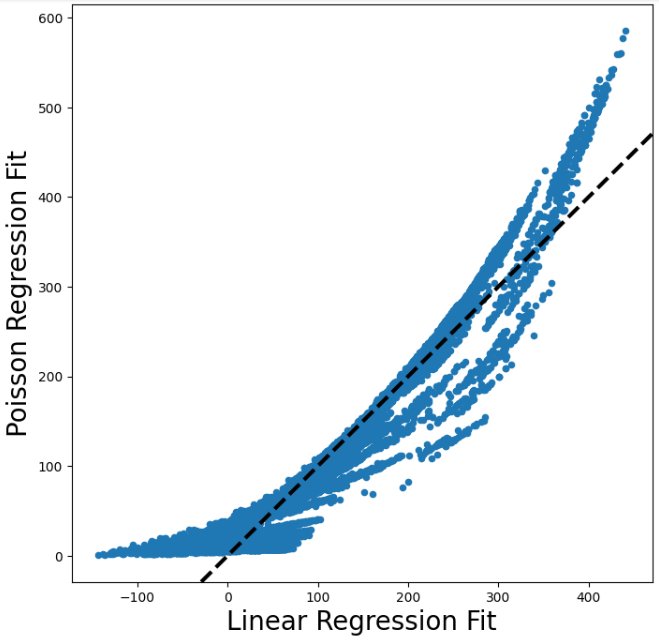

대여량이 낮거나 높은 영역에선 포아송이 더 높게 예측하는 경향이 있고, 그렇지 않은 영역에선 더 낮게 예측하는 경향이 있다.

Reference: An Introduction to Statistical Learning: with Applications in Python by Gareth James

profile
조성호
즐겁게 살자
이전 포스트

Single Layer Neural Networks

0개의 댓글