EDA & DataViz

AAiss·2024년 8월 23일

AI Basics

목록 보기

11/12

서론

현대의 데이터 분석과 머신러닝 모델링은 "데이터를 얼마나 잘 이해하고 다룰 수 있는가"에서 시작된다.
데이터는 단순한 숫자나 문자의 나열이 아니라, 그 안에 담긴 패턴과 의미를 해석하고 활용하는 것이 핵심이다.

본 포스팅에서는 데이터를 여러 관점에서 분류하고 설명하며, 각 데이터 유형의 특징과 전처리 방법, 분석 기법을 다룬다.
정형 데이터부터 시계열, 이미지, 텍스트 데이터까지 다양한 형태의 데이터를 폭넓게 이해할 수 있도록 구성하였다.

데이터

의사결정을 돕기 위해 수집된 정보, 특히 사실 또는 숫자, 또는 컴퓨터에 의해 저장되고 사용될 수 있는 전자적 형태의 정보

- Cambridge Dictionary -

정형 데이터

범주형 데이터

숫자로 측정하고 표시하는 것이 불가능한 자료

명목형 데이터

순서 없이 항목으로 구분되는 데이터
ex) 성별, 국가, 과일 종류 등

순서 정보를 모델에 주입하지 않기 위해 One-Hot Encoding 사용

sklearn.preprocessing.OneHotEncoder()

순서형 데이터

각 값의 우위 등 순서가 존재하는 데이터
ex) 리커트 척도, 영화 별점표 등

순환형 데이터

순서는 있지만 해당 값이 순환하는 데이터
ex) 각도, 요일 등

수치형 데이터

숫자 형태로 측정되는 자료

이산형 데이터

정수 형태를 띄고 있는 데이터
ex) 인구 수, 횟수 등

연속형 데이터

실수 형태를 띄고 있는 데이터
ex) 키, 몸무게 등

정규화(Normalization)

데이터의 범위를 [0, 1] 또는 [-1, 1]과 같은 특정 범위로 변환

A = [-10, -5, 3, 12, 90]

1. 모든 요소 - 최솟값: A = [0, 5, 13, 22, 100]
2. 모든 요소 / (최댓값 - 최솟값): A = [0, 0.05, 0.13, 0.22, 1]

표준화(Standardization)

데이터의 평균을 0, 표준편차를 1로 만들어, 데이터를 표준 정규 분포 형태로 변환

A = [-10, -5, 3, 12, 90]

1. 모든 요소 - 평균: A = [-28, -23, -15, -6, 72]
2. 모든 요소 / 표준편차(std): A = [-0.761, -0.626, -0.408, -0.163, 1.957]

대칭성

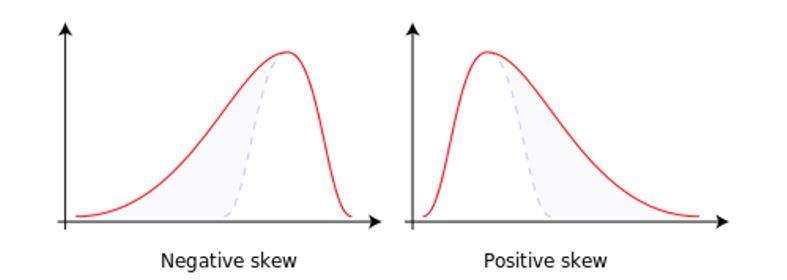
출처: https://en.m.wikipedia.org/wiki/File:Negative_and_positive_skew_diagrams_%28English%29.svg.

Negative skew

데이터가 큰 값에 집중되어 있고, 상대적으로 작은 값들이 적음

큰 값들이 있는 구간의 범위를 축소하여, 큰 값의 영향을 줄여야 함

Square/Power Transformation: 제곱 변환 또는 거듭 제곱

Exponential Transformation: 지수

Positive skew

데이터가 작은 값에 집중되어 있고, 큰 값들이 상대적으로 적음

작은 값들이 있는 구간의 범위를 확대하여, 작은 값의 영향을 줄여야 함

Log Transformation: 로그

Square-root Transformation: 제곱근

결측치

데이터셋에 누락된 값 (Null, NA)

결측치는 제외 또는 예측을 통해 처리

결측치 처리 기준

결측치가 과반수인 경우
– 결측치 유무만 사용
– 결측치 데이터 포함 열 제외

결측치가 유의미하게(>5%) 많은 경우
– 결측치 정보가 유의미한 정보임을 우선 파악
– 결측치를 채우기 위한 대푯값 전략

결측치의 개수가 매우 적은 경우
– 결측치가 포함된 행의 값을 미포함하는 경우도 고려 가능
– 결측치를 위한 대푯값 계산 필요

결측치 예측

규칙 기반
– 도메인 지식이나 논리적 추론에 의한 방법
– 지나치게 복잡하거나 단순한 경우 잘못된 편향이 반영될 수 있음

집단 대푯값
– 특정 집단의 대푯값(평균, 중앙값, 최빈값) 등 사용
– 집단 설계가 중요하고 이상치에 민감할 수 있음

모델 기반
– 회귀모델을 포함한 다양한 모델을 통해 예측
– 복잡한 패턴을 예측할 수 있으나 과적합 이슈 발생 가능

이상치

관측된 데이터의 범위에서 과하게 벗어난 값

명확한 기준은 없으나 대표적으로 사용되는 기준 존재

IQR (Inter Quantile Range)

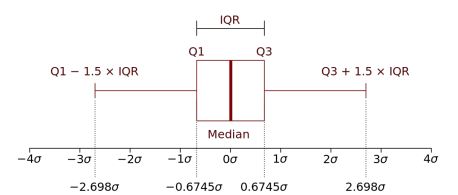
출처: https://en.wikipedia.org/wiki/Interquartile_range

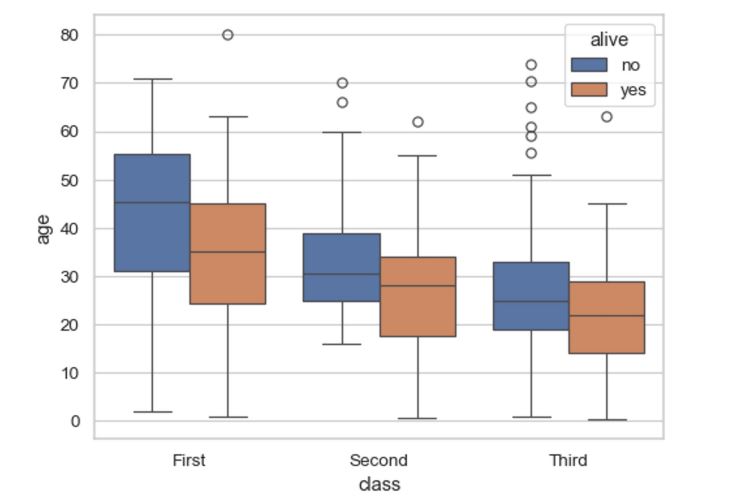
출처: https://seaborn.pydata.org/generated/seaborn.boxplot.html

특성 추출

특성 간의 결합을 통해 새롭게 특성을 만들어 내는 과정

사칙 연산을 통해 값을 연산

아들의 수와 딸의 수가 별개로 있다면 => 합쳐서 자녀의 수로 새로운 피쳐 추출

범주와 범주, 범주와 수치 간의 연결을 통해 새로운 범주를 만들고 LabelEncoding

국가와 나이대에 따라 연결하고 이를 범주형으로 변경 => 한국20, 중국30=> 1,2

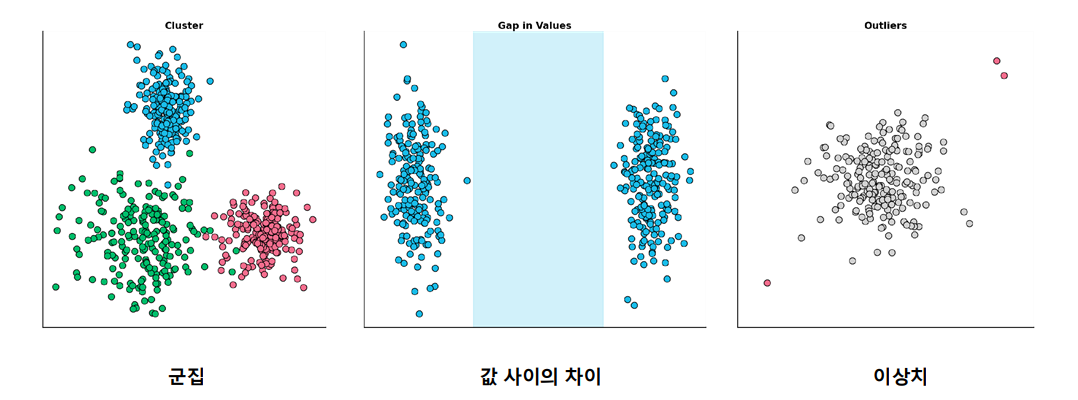
클러스터링

유사한 성격을 가진 데이터를 그룹으로 분류하는 것

데이터 전 과정에서 유의미하게 사용 가능

[관찰] EDA작업에서 대략적인 그룹에 대한 확인

[모델] 모델에 사용할 새로운 피쳐 (특성 추출)

[해석 및 결정] 최종 그룹 구분 및 의사 결정

K-Mean: 그룹을 K개로 그룹화하여, 각 클러스터의 중심점을 기준으로 데이터 분리

Hierarchical Clustering: 데이터를 점진적으로 분류

DBSCAN: 밀도 기반 클러스터링

GMM: 가우시안 분포가 혼합된 것으로 모델링

차원 축소

특성 추출 방법 중 하나로 데이터의 특성(feature) N개를 M개로 줄이는 방법을 통칭

데이터 복잡성 감소: 고차원 데이터 => 저차원 데이터

시각화: 패턴 발견에 용이 => 클러스터링과 매우 밀접한 관련

모델 성능 향상

차원 축소 방법

정보를 최대한 보유하고, 왜곡을 최소화해야 함

가까운 데이터는 최대한 가깝게, 먼 데이터는 최대한 멀게

PCA: 데이터의 공분산을 계산하여 고유 벡터를 찾아 투영

t-SNE: 데이터 포인트 간 유사성을 모델링하여 저차원 공간에 재현

UMAP: 위상 구조의 정보를 최대화하여 저차원 공간에 재현

LDA: 클래스 간 분산을 최대화하고, 클래스 내 분산을 최소화하는 방식

Isomap: 고차원에서 최단 경로 거리에 대한 정보를 저장

Autoencoder: 인코더/디코더 구조로 고차원 데이터의 정보를 최대한 저장한 저차원 공간

시계열 데이터

하나의 변수를 시간에 따라 여러 번 관측한 데이터

가격, 매출, 온도, 성장 등 변화 예측과 반복되는 패턴에 대한 인사이트 도출이 목표

단순히 값 뿐만 아니라 변동성 등에 대한 다양한 예측 가능

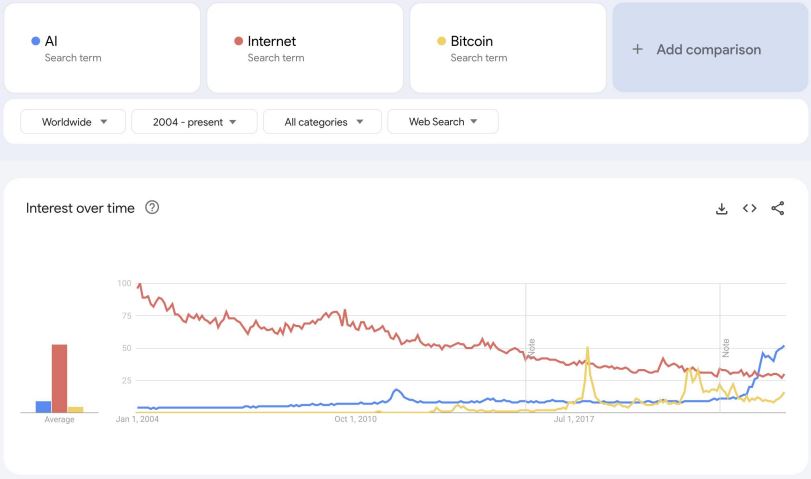
출처: https://trends.google.com/trends/

특징

추세(trend): 장기적인 증가 또는 감소

계절성(seasonality): 특정 요일/계절에 따라 영향

주기(cycle): 고정된 빈도가 아니지만 형태적으로 유사하게 나타나는 패턴

노이즈(noise): 측정 오류, 내부 변동성 등 다양한 요인으로 생기는 왜곡

분석 방법

가법모델(additive model): 추세 + 계절성 + 주기 + 노이즈

승법모델(multiplicative model): 추세 x 계절성 x 주기 + 노이즈

시간에 따라 변동폭이 비교적 일정하다면 가법모델, 변동폭이 커진다면 승법모델 사용

정상성 & 비정상성

대부분의 시계열 데이터는 시간에 따라 통계적 특성이 변함(물가, 가격, 사용자수 등)

정상성: 시간에 따라 통계적 특성이 변하지 않음

비정상성: 시간에 따라 통계적 특성이 변함

비정상성 처리

차분(Differencing): 이웃된 두 값의 차이값을 사용

[1, 2, 4, 7, 8, 10] => [None, 1, 2, 3, 1, 2]

경우에 따라 2차 차분도 가능

바로 직전 데이터가 아닌 계절성 주기에 따라 차이를 두는 계절성 차분도 존재

로그 연산: 로그 연산을 통해 비정상성 일부 제거 가능

시계열 데이터 전처리

평활(Smooting): 데이터의 불필요한 변동을 제거하여 쉬운 해석을 돕는 것

평활의 목적

추세 및 계절성 파악: 노이즈 감소로 쉬운 추세와 계절성 파악

데이터 시각화 개선: 시각적 해석에 용이

구간별 평균/구간별 통계 사용

구간으로 나누어 통계값 사용

데이터 개수가 줄어들 수 있어 관찰에만 용이

이동평균(Moving Average)

이전 데이터의 총 평균을 주기별로 움직여가며 사용

그 외 이동평균

최신 데이터에 더 가중치를 두기 위한 방법

가중 이동평균(Weighted Moving Average,WMA): 가중치 기반

지수 이동평균(Exponential Moving Average,EMA): 지수함수로 가중치 계산

이동평균

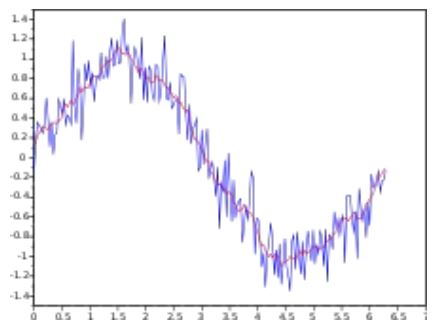
지수 이동평균

이미지 데이터

픽셀(pixel)이라고 하는 작은 이미지를 직사각형 형태로 모은 것

이미지 데이터 EDA

[Target 중심] 분포 위주의 초기 비교(정형 데이터 해석)

범주 또는 값의 분포가 균등하지 않고 편향되어 있는 경우

특정 범주의 이미지가 지나치게 적은 경우

전체 이미지 개수가 적은 경우

[Input 중심] 이미지 데이터의 개별 비교(도메인 지식)

[Process 중심] 전처리-모델-결과해석 반복

이미지 데이터 저장 방식

RGB: 빛의 삼원색(빨강,초록,파랑)의 합으로 색을 표현

HSV: 인간의 색인지와 유사(Hue, Saturation, Value = 색상, 채도, 명도)

CMY(K): RGB의 보색, 일반적으로 인쇄에 용이

YCbCr: 밝기 / 파랑에 대한 색차 / 빨강에 대한 색차로 구분하여 디지털 영상에 용이

이미지 포맷

JPEG(Join Photographic Expert Group): 손실 압축 방법론

웹 게시용에 사용

YCbCr을 사용하며, 양자화를 통해 일부 손실 압축

PNG(Portable Network Graphics): 무손실 압축 방법

투명도를 포함할 수 있음

WepP: 구글이 만든 이미지 포맷

위 둘의 방식을 포함할 수 있음

SVG(Scalable Vector Graphics): 벡터 이미지를 통한 저장

방식과 크기에 무관한 저장, 로고 등에 적합

이미지 데이터 전처리

목적

데이터 퀄리티 향상

데이터 양 증대

시각화를 통한 인지 개선

방법

색상 공간(Color Space):RGB, HSV, Grayscale

노이즈 삽입(Noise)

사이즈 조정(Resizing): Crop & Interpolation

아핀 변환(Affine Transformation): 회전, 왜곡, 평행이동 등

특성 추출(FeatureExtraction): SIFT, SURF, ORB, FAST 등

라이브러리

OpenCV: 효율적인 처리. 복잡한 사용

BGR 순서로 데이터 저장. H x W로 저장

PIL(Python Image Library => Pillow): 쉬운 이미지 전처리 기능 모두 제공

RGB 순서로 데이터 저장. W x H로 저장

scikit-image: SciPy 기반 이미지 처리

scikit-learn과 유사한 포맷으로 쉬운 사용

albumentations: 이미지 전처리용 라이브러리

일반적으로 데이터 증강 등에 활용

torchvision: torch 기반 이미지 전처리

SciPy: 대부분의 기능적 요소 탑재

다만 사용성이 다른 라이브러리에 비해 아쉬움

텍스트 데이터

특징

언어는 구조에 따라 의미가 변경될 수 있음

구조가 달라도 의미가 같을 수 있음

언어에 따라 구조가 다름

문법에는 다양한 규칙이 존재

문장에는 필요 없는 표현도 존재

일부러 오타를 사용 및 활용하는 경우도 있음

방언,신조어 등이 포함될 수 있음

개인정보가 포함될 수 있음

의미가 시기적, 사회적으로 달라질 수 있음

전처리

정규표현식

문자열의 특정한 패턴을 표현하는 방법

Ex) 이메일: [a-zA-Z0-9]+@[a-zA-Z0-9]+.[a-zA-Z]{2,}

토큰화

1) 선택적 전처리(cleansing): 대소문자 통일, 불필요한 문자 제거, 철자 교정
2) 문단/문장 토큰화: 마침표, 물음표 등 특수부호를 통한 구분
3) 단어 토큰화: 공백, 쉼표 등을 통한 구분
4) 서브워드 토큰화: 복합어/합성어 등의 구분
5) 불용어 제거(stopword): 문맥적으로 의미 없는 표현 제거
6) 어간추출 & 표제어 추출(stemming & lemmatization)
- 표제어: 언어의 원형(are,is => be)
- 어간 추출: 형태학적 언어에서 어간 추출(beginning => begin)

데이터 시각화

Bar Plot

직사각형 막대를 사용하여 데이터의 값을 표현하는 차트/그래프

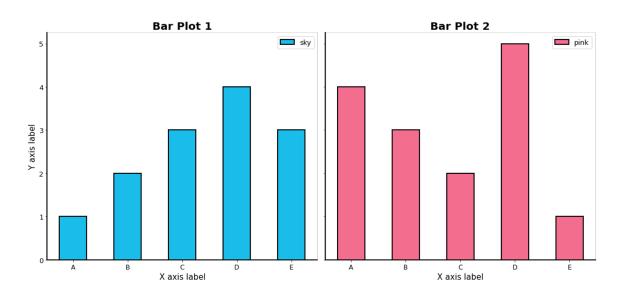
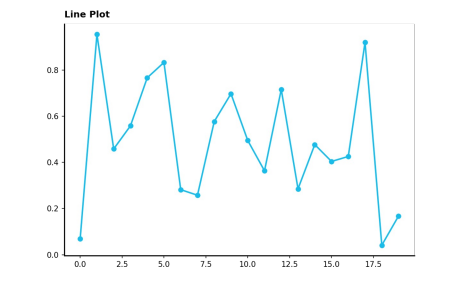
Line Plot

연속적으로 변화하는 값을 순서대로 점으로 나타내고, 이를 선으로 연결한 그래프

Scatter Plot

점을 사용하여 두 feature간의 관계를 알기 위해 사용하는 그래프

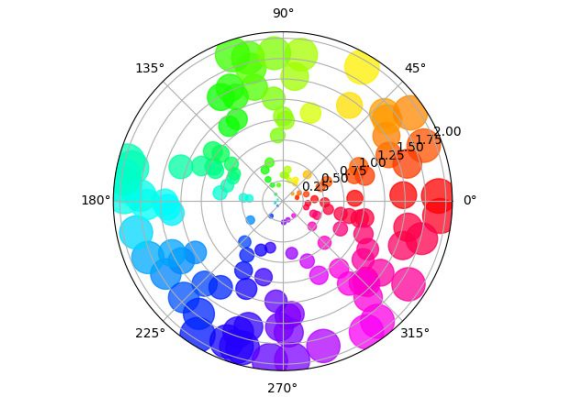
Polar Plot

극 좌표계(Polar Coordinate)를 사용하는 시각화

회전, 주기성 등 표현에 적합

Radar Chart

극 좌표계를 사용하는 대표적인 차트

중심점을 기준으로 N개의 변수값을 표현할 수 있음

각 feature는 독립적이며, 척도가 같아야 함

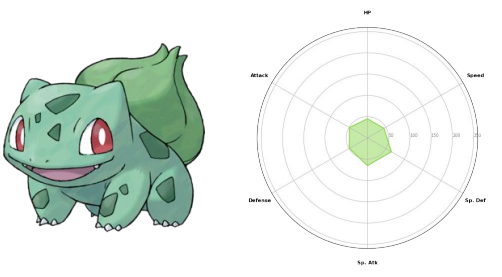출처: https://bulbapedia.bulbagarden.net/wiki/Bulbasaur_(Pok%C3%A9mon)

Pie Chart

원을 부채꼴로 분할하여 표현하는 통계 차트

전체를 백분율로 나타낼 때 유용

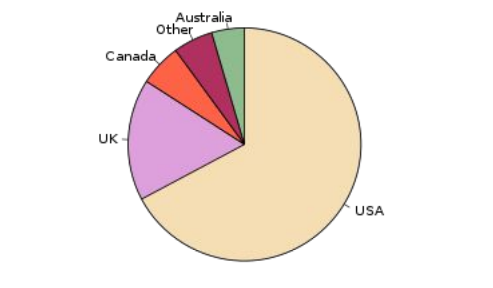출처: Pie chart of populations of English native speakers | wikipedia

Donut Chart

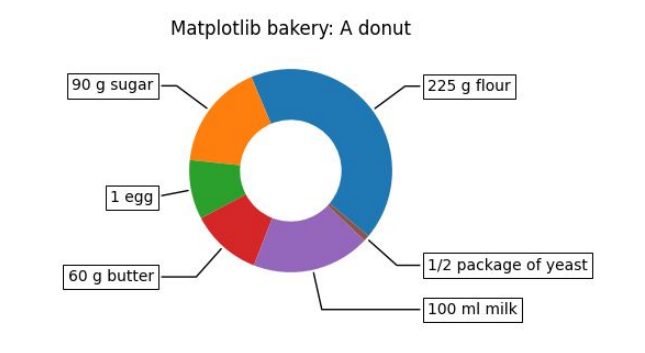
Sunburst Chart

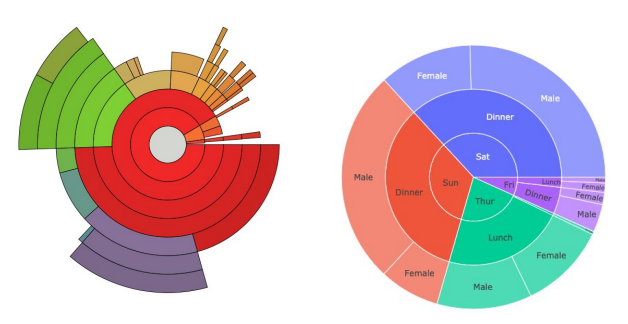
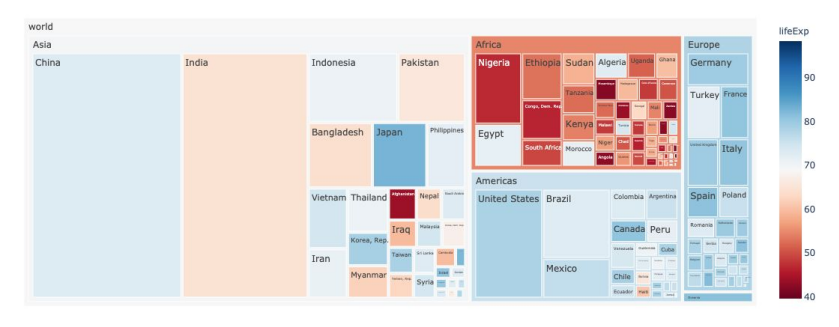
Treemap

계층 데이터에 대해 직사각형을 사용하여 포함 관계를 표현

사각형을 분할하는 타일링 알고리즘에 따라 형태가 다양

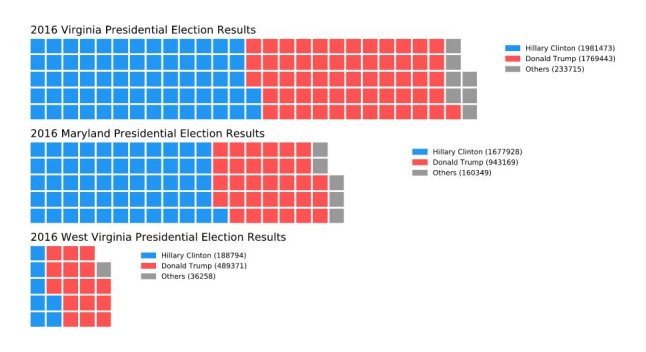
Waffle Chart

와플 형태로 discrete 하게 값을 나타내는 차트

기본적인 형태는 정사각형이나 원하는 벡터 이미지로도 사용 가능

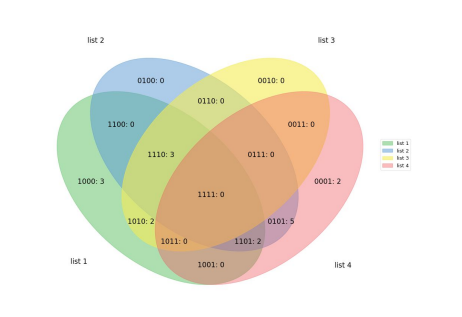
Venn

집합(set) 등에서 사용하는 익숙한 벤 다이어그램

EDA보다는 출판 및 프레젠테이션에 사용

결론

이번 포스팅에서는 데이터를 유형별로 분류하고, 각 유형의 특징과 전처리 및 분석 방법을 정리하였다.
데이터의 형태에 따라 필요한 접근 방식과 처리 기법이 달라지며, 이는 모델의 성능과 해석 가능성에 큰 영향을 미친다.

따라서 데이터를 단순히 입력으로 바라보지 않고, 데이터 자체에 대한 깊은 이해를 바탕으로 분석에 접근하는 것이 중요하다.
데이터 전처리, 시각화, 이상치 탐지, 결측치 처리 등의 기초 작업은 그 자체로도 충분히 가치 있으며, 최종 결과의 품질을 좌우하는 핵심 요소임을 잊지 말자.

AAiss

이전 포스트

Neural Network

다음 포스트