Neural Network

서론

인공신경망(Neural Network)은 인간의 뇌 구조에서 영감을 받아 개발된 머신러닝 알고리즘으로, 복잡한 패턴 인식과 데이터 분석에 뛰어난 성능을 발휘한다.

특히, 최근 몇 년 간 딥러닝 기술의 발전으로 인해 다양한 분야에서 인공신경망의 활용이 급증하고 있다.

본 포스팅에서는 퍼셉트론(Perceptron)부터 시작해 단층 및 다층 퍼셉트론(Multiple Layer Perceptron, MLP), 활성화 함수(Activation Functions)와 역전파(Back Propagation) 알고리즘까지, 신경망의 기초 개념과 구조를 설명할 것이다.

---

Perceptron

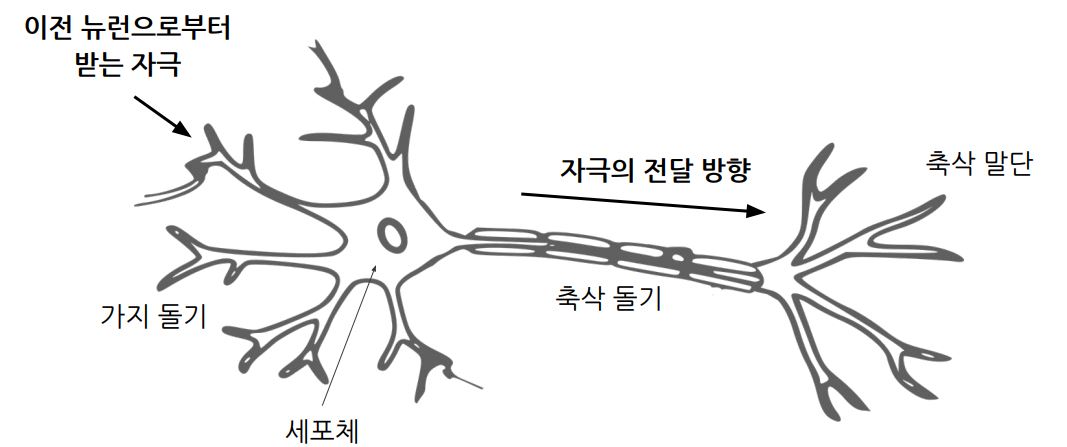
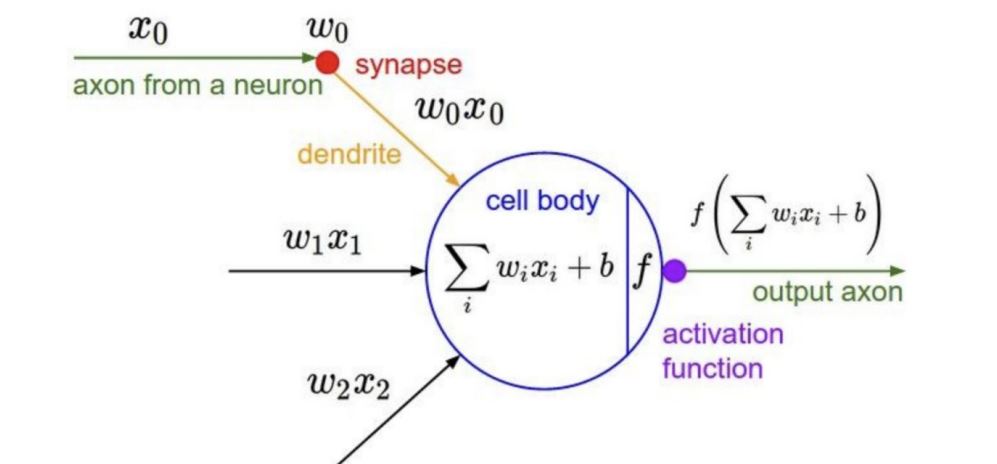
두뇌의 신경세포, 즉 뉴런이 연결된 형태를 모방한 모델

출처: https://svgsilh.com/ko/image/2022398.html

출처: https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture4.pdf

---

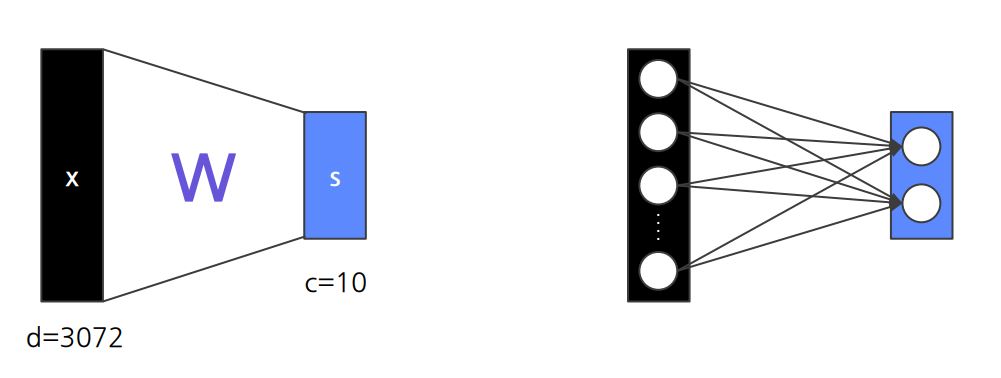
Single Layer Perceptron

$f(x) = Wx$

---

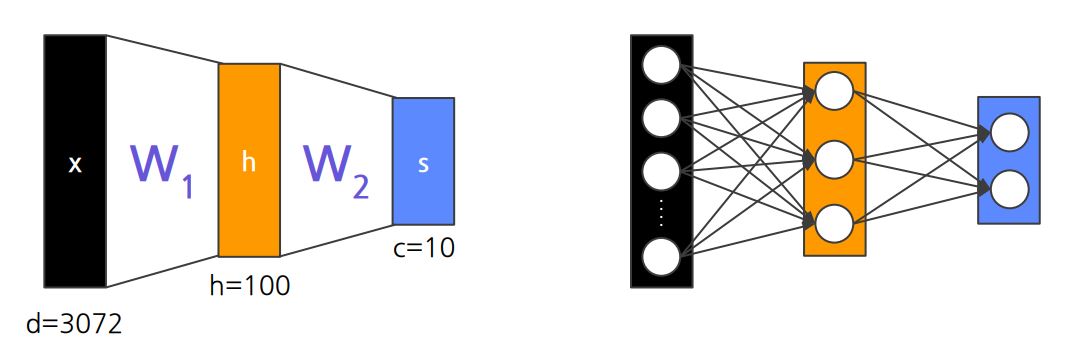
Multiple Layer Perceptron (MLP)

• $f(x) = W_2(W_1x)$
• $W_2W_1 = W$ 즉, Multiple Layer는 여전히 Linear
• 이를 해결하기 위해 Activation function을 통해 Hidden Layer(은닉층) 필요
• $f(x) = \sigma_2(W_2\sigma_1(W_1x))$

---

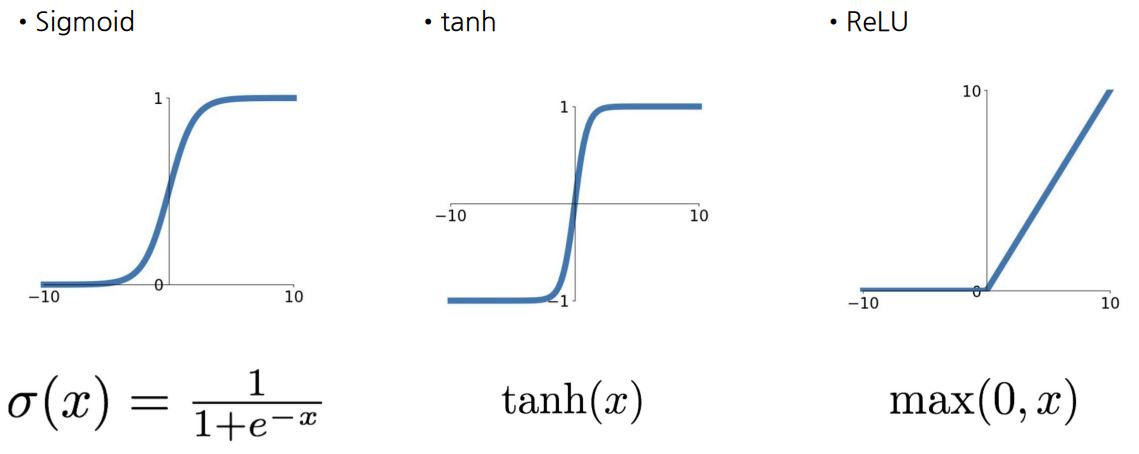
Activation Functions

• 입력 신호의 가중합을 계산한 후, 이 가중합에 활성화 함수를 적용하여 뉴런의 최종 출력을 생성
• 신경망의 비선형성을 도입하여 복잡한 패턴을 학습할 수 있도록 지원

---

Sigmoid

특징

• 출력값의 범위: [0, 1]
• 가장 많이 사용 되었던 함수

단점

• Vanishing Gradient: input이 크거나 작을 때 기울기가 0에 가까워짐
• zero-centered X
• exp()의 연산 비용이 큼

---

Tanh

특징

• 출력값의 범위: [-1, 1]
• Zero-centered

단점

• Vanishing Gradient가 여전히 발생
• 확장된 Sigmoid

---

ReLU (Rectified Linear Unit)

특징

• (+) 영역에서 Saturate(특정 값에 고정되어 더 이상 변화하지 않는 상태) X
• 연산이 효율적
• Sigmoid, Tanh보다 빠르게 수렴

단점

• zero-centered X
• (-) 영역에서 Saturate
• $x = 0$일 때, 미분 불가능

---

Leaky ReLU

특징

• 모든 영역에서 Saturate X
• 연산이 효율적
• Gradient Vanishing 발생 X

단점

• zero-centered X
• (-) 영역에서 Saturate
• 추가적인 하이퍼파라미터 필요 ($x < 0$일 때의 기울기)

---

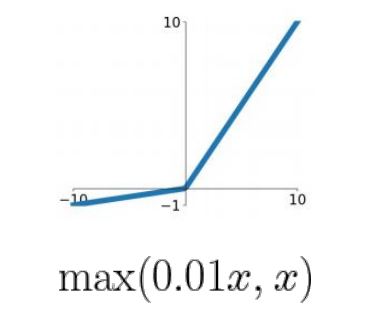
ELU (Exponential Linear Unit)

특징

• ReLU의 모든 장점 포함
• (Leaky)ReLU에 비해 Saturated된 (-) 영역이 더욱 Robust(견고)

단점

• exp()의 연산 비용이 큼

---

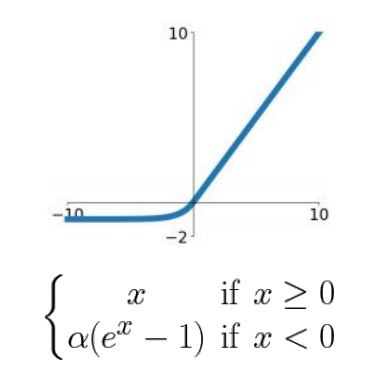
Tip

• (학습률에 주의하며) 주로 ReLU 사용
• Sigmoid, Tanh는 필요시 Last Layer에만 사용

---

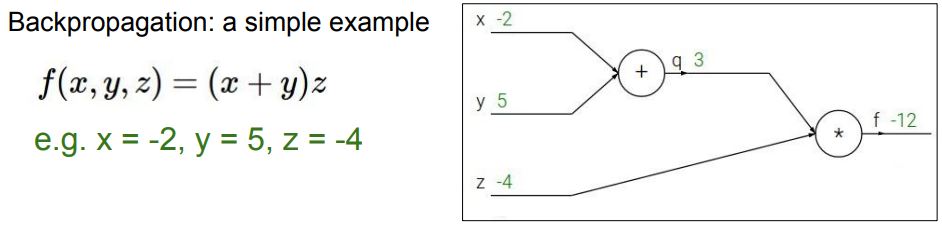
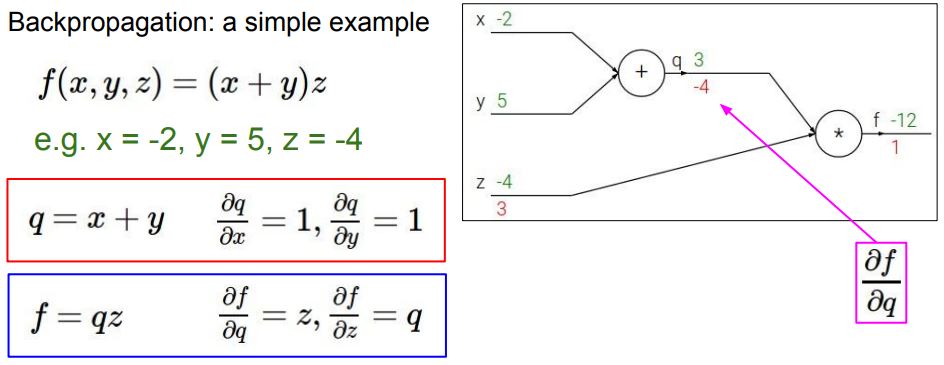
Back Propagation

• 손실에 대한 기울기를 계산하고 이를 기반으로 가중치를 업데이트
• 업데이트 시 학습률이 중요하게 작용함
• Adam Optimizer가 압도적 성능

---

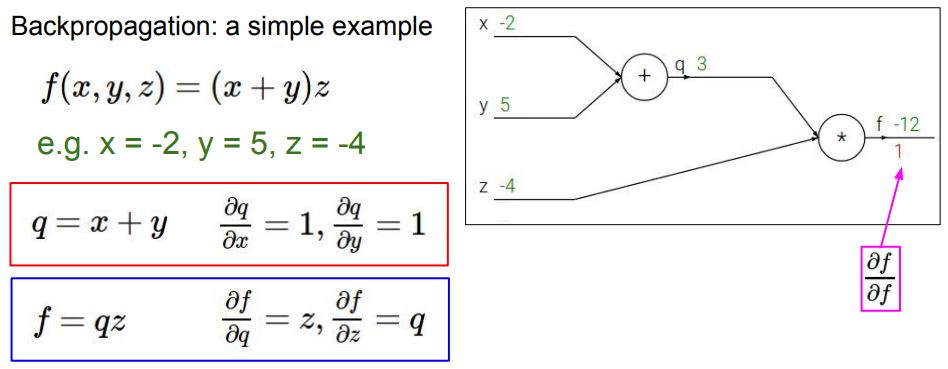
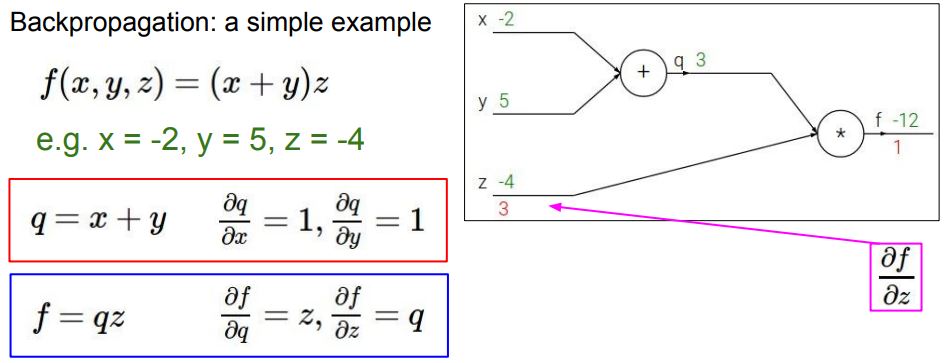
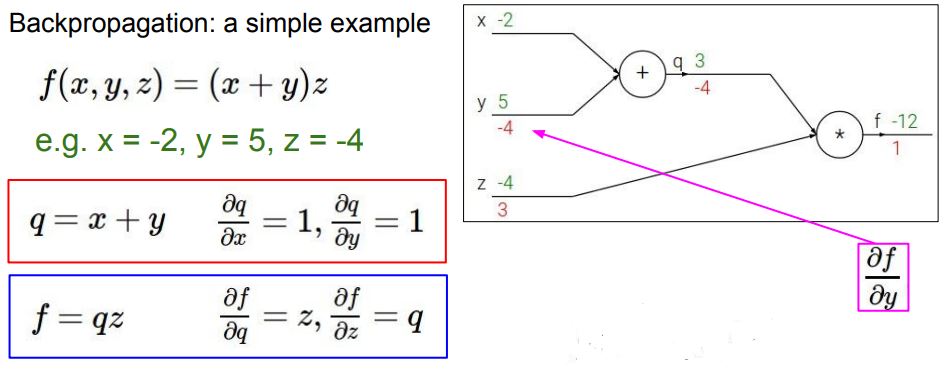
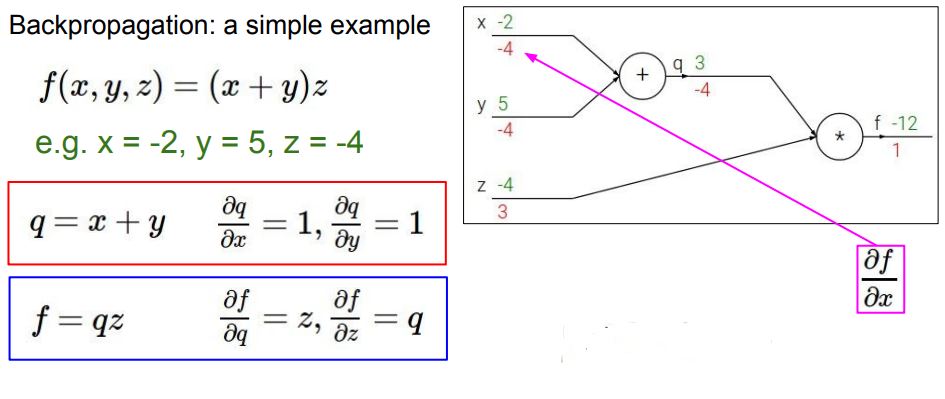
계산 과정

출처: https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture4.pdf

$x_{new} = x_{old} - 0.01 \cdot (-4) = -2 + 0.04 = -1.96$
$y_{new} = y_{old} - 0.01 \cdot (-4) = 5 + 0.04 = 5.04$
$z_{new} = z_{old} - 0.01 \cdot (3) = -4 - 0.03 = -4.03$

Forward Propagation, Back Propagation을 반복하여 loss 값이 점차 감소

---

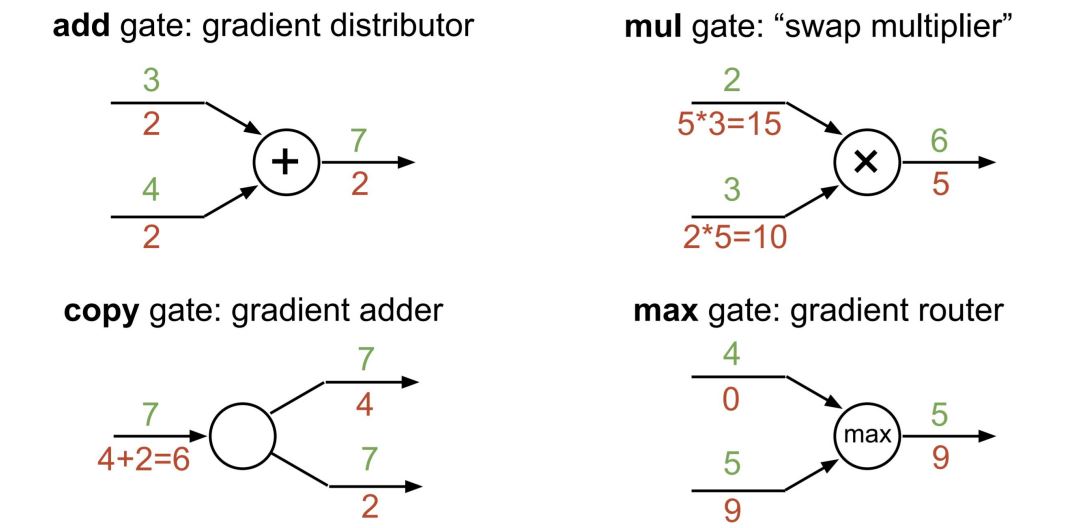
Tip

출처: https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture4.pdf

---

결론

이번 포스팅에서는 인공신경망의 기본 구조와 작동 원리를 살펴보았다.

퍼셉트론에서 시작하여 다층 퍼셉트론과 다양한 활성화 함수, 그리고 역전파 알고리즘의 중요성을 강조했다.

이러한 요소들은 신경망의 성능과 효율성을 결정짓는 핵심 요소로, 각 알고리즘과 함수의 특성을 이해하는 것이 필수적이다.

---