Linear Regression

AAiss·2024년 8월 12일

AI Basics

목록 보기
5/12
post-thumbnail

서론

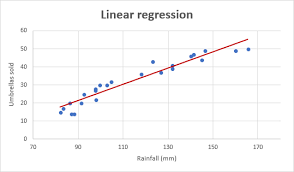
선형 회귀는 통계학과 머신러닝 분야에서 가장 기본적이면서도 중요한 기법 중 하나이다.

데이터 간의 관계를 모델링하고 예측하는 데 사용되는 이 기법은 간단한 수학적 원리에 기반하여 직선 형태의 함수로 데이터 포인트를 설명한다.

본 포스팅에서는 선형 회귀의 개념부터 시작하여, 데이터 전처리, 모델 학습, 그리고 테스트까지 단계별로 살펴볼 것이다.

선형 회귀

  • 트레이닝 데이터를 통해 특징 변수와 목표 변수 간의 선형 관계 분석
  • 이를 바탕으로 모델 학습, 테스트 데이터의 결과를 연속적인 값으로 예측

데이터 전처리

  • 데이터 분석을 위해 데이터를 분석에 적합한 형태로 가공하는 과정
  • 불필요한 데이터 제거하고, 결측치나 이상치를 처리하여 데이터의 질 향상
  • 특징 변수(xx) - YearsExperience
  • 목표 변수(tt) - Salary

사용 데이터셋: Salary Dataset
저작권 정보: CC0 1.0 Universal

데이터 로드

# Donwload dataset from kaggle
!kaggle datasets download -d abhishek14398/salary-dataset-simple-linear-regression
# unzip zip file
!unzip salary-dataset-simple-linear-regression.zip
import pandas as pd

data = pd.read_csv("Salary_dataset.csv", sep = ",", header = 0)

특징 변수와 목표 변수 분리

x = data.iloc[:, 1].values # x: YearsExperience
t = data.iloc[:, 2].values # t: Salary

데이터 표준화

특징 변수 값과 목표 변수 값의 차이가 클 때 두 변수의 평균을 0, 분산을 1로 표준화

from sklearn.preprocessing import StandardScaler

scaler_x = StandardScaler()
x_scaled = scaler_x.fit_transform(x.reshape(-1, 1))

scaler_t = StandardScaler()
t_scaled = scaler_t.fit_transform(t.reshape(-1, 1))

Tensor로 변환

# nn.Module 클래스 사용을 위해 1차원 numpy 배열을 2차원 Tensor로 변환
x_tensor = torch.tensor(x_scaled, dtype=torch.float32).view(-1, 1)
t_tensor = torch.tensor(t_scaled, dtype=torch.float32).view(-1, 1)

상관관계 분석

rxt=∑i=1n(xi−xˉ)(ti−tˉ)∑i=1n(xi−xˉ)2∑i=1n(ti−tˉ)2r_{xt} =\frac{\displaystyle\sum_{i=1}^{n}{(x_i-\bar{x})(t_i-\bar{t})}} {\sqrt{\displaystyle\sum_{i=1}^{n}{(x_i-\bar{x})^2}\displaystyle\sum_{i=1}^{n}{(t_i-\bar{t})^2}}}　　　　(표본상관계수)

  • −1 ≤ rxt ≤ 1-1\ \le\ r_{xt}\ \le\ 1
    • ∣rxt∣|r_{xt}|가 1에 가까울수록 상관 관계 높음
    • ∣rxt∣|r_{xt}|가 1에 가까울수록 상관 관계 낮음

  • rxt≈1r_{xt} \approx 1 (양의 상관)
    • 기온과 아이스크림 판매량: 기온이 상승하면 아이스크림 판매량도 증가

  • rxt≈−1r_{xt} \approx -1 (음의 상관)
    • 기온과 난방비: 기온이 하강하면 난방비는 증가

참고: https://datascienceschool.net/02%20mathematics/07.05%20%EA%B3%B5%EB%B6%84%EC%82%B0%EA%B3%BC%20%EC%83%81%EA%B4%80%EA%B3%84%EC%88%98.html

  • np.corrcoef(x, t)
    • xx와 tt의 상관계수 반환
import numpy as np

correlation_matrix = np.corrcoef(x, t)
correlation_coefficient = correlation_matrix[0, 1]

print(correlation_matrix)

print('Correlation Coefficient:', correlation_coefficient)

[[1. 0.97824162]
[0.97824162 1. ]]

Correlation Coefficient: 0.9782416184887599

상관관계 시각화

  • plt.scatter(x, t)
    • xx와 tt의 상관 관계를 산점도로 시각화
import matplotlib.pyplot as plt

plt.scatter(x, t)
plt.xlabel('YearsExperience')
plt.ylabel('Salary')
plt.title('YearsExperience vs Salary')
plt.grid(True)
plt.show()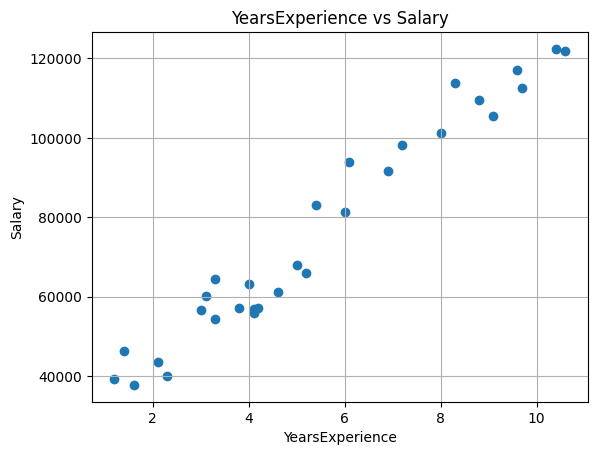

모델 학습

  • 트레이닝 데이터의 특성을 가장 잘 표현할 수 있는 직선 탐색
    • 직선: y=wx+by = wx + b
    • 최적의 ww (가중치)와 bb (바이어스) 탐색

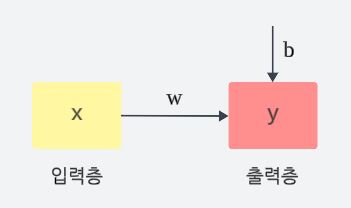
선형 회귀 모델 (by 신경망)

  • 입력층: 특징 변수들(xx)
  • 출력층: 예측 변수(yy)
  • nn.Module
    • 신경망의 모든 계층을 정의하기 위한 기본 클래스
    • nn.Module 클래스를 상속하여 선형 회귀 모델 생성 가능

장점

  • 일관성: 모든 신경망 모델을 같은 방식으로 정의 및 사용
  • 모듈화: 모델을 계층별로 나누어 관리하므로 코드가 깔끔함
  • GPU 지원: 대규모 연산을 가속화하여 모델의 학습 속도 향상
import torch.nn as nn

class LinearRegressionModel(nn.Module):
    def __init__(self):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(1, 1)  # 입력 Tensor 차원, 출력 Tensor 차원 모두 1인 선형 회귀 모델

    def forward(self, x_tensor):
        y = self.linear(x_tensor) # y = wx + b
        return y
        
model = LinearRegressionModel()
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

model.to(device) # 모델을 GPU로 전송
x_tensor = x_tensor.to(device) # 입력 데이터를 GPU로 전송
t_tensor = t_tensor.to(device) # 정답 데이터를 GPU로 전송

손실함수

  • 목표 변수(tt)와 예측 변수(yy) 간의 차이를 측정하는 함수
  • 모델 최적화를 위해 사용
  • 손실 함수의 값이 크다면 목표 변수와 예측 변수의 평균 오차가 큼 😢
  • 손실 함수의 값이 작다면 목표 변수와 예측 변수의 평균 오차가 작음 😊

오차는 음수와 양수 모두 존재할 수 있기 때문에 오차의 절댓값 혹은 제곱을 이용

MSE(Mean Squared Error)

Loss Function=1n∑i=1n[ti−yi]2=1n∑i=1n[ti−(wxi+b)]2Loss\ Function = \frac{1}{n}\displaystyle\sum_{i=1}^{n}[t_i - y_i]^2 = \frac{1}{n}\displaystyle\sum_{i=1}^{n}[t_i - (wx_i + b)]^2

  • nn.MSELoss()
    • MSE 손실함수

경사하강법

  • 머신러닝의 최적화(Optimization) 알고리즘 중 하나
  • 손실함수에서 모델의 w (가중치)와 b (바이어스)의 최적의 값을 찾기 위해 사용

w∗=w−α∂l(w,b)∂ww^* = w - \alpha\frac{\partial l(w,b)}{\partial w}
　　　　　　　　　　　　　　 α:\alpha: 학습률
b∗=b−α∂l(w,b)∂bb^* = b - \alpha\frac{\partial l(w,b)}{\partial b}

  • 모든 데이터를 사용하여 가중치와 바이어스를 업데이트하기 때문에 계산이 정확하고 안정적
  • 하지만, 데이터가 많을 경우 계산 비용이 높아지며 특히 대규모 데이터셋에 비효율적
  • 전체 데이터셋의 기울기를 평균 내어 계산하므로 Local Minima에 갇힐 가능성 높음

확률적 경사하강법 (SGD)

  • 각 데이터 포인트마다 오차를 계산하여 가중치와 바이어스를 업데이트하는 최적화 알고리즘
  • 각 데이터 포인트의 기울기를 계산하므로 이 과정에 노이즈가 포함되어 Global Minima 도달 용이
  • optimizer.zero_grad()
    • 이전 단계에서 계산된 경사(기울기) 초기화

  • loss.backward()
    • 현재 손실 값에 대한 경사(기울기)를 자동 미분

  • optimizer.step()
    • 계산된 기울기(경사)를 사용하여 가중치 𝑤값을 업데이트
import torch.optim as optim

loss_function = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr = 0.01)  # 학습률은 적절히 설정

y = model(x_tensor)  # 순전파
loss = loss_function(y, t_tensor)  # 손실 값 계산

loss.backward()  # 역전파
optimizer.step()  # 계산된 경사(기울기)를 사용하여 가중치 업데이트
optimizer.zero_grad()  # 이전 단계에서 계산된 경사(기울기) 0으로 초기화

에폭 (Epoch)

  • 모델이 전체 데이터셋을 한 번 완전히 학습하는 과정
  • 에폭이 너무 크면 과대적합(Overfitting) 발생 가능
  • 에폭이 너무 작으면 과대적합(Underfitting) 발생 가능

과대적합 (Overfitting)

트레이닝 데이터셋에 지나치게 최적화되어 테스트 데이터셋에 대해 낮은 성능 😥

과소적합 (Underfitting)

트레이닝 데이터셋에 최적화가 제대로 되지 않아 낮은 성능 😥

num_epochs = 1000
loss_list = []

for epoch in range(num_epochs):
    y = model(x_tensor)  # 순전파
    loss = loss_function(y, t_tensor)  # 손실 값 계산

    loss.backward()  # 역전파
    optimizer.step()  # 계산된 경사(기울기)를 사용하여 가중치 업데이트
    optimizer.zero_grad()  # 이전 단계에서 계산된 경사(기울기) 0으로 초기화

    loss_list.append(loss.item())  # 손실 값 저장

    if (epoch+1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item()}')       

        for name, param in model.named_parameters():  # 디버깅 정보 출력
            print(f'{name}: {param.data}')
import matplotlib.pyplot as plt

plt.figure()
plt.plot(loss_list, label='Train Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)
plt.title('Loss Trend')
plt.show()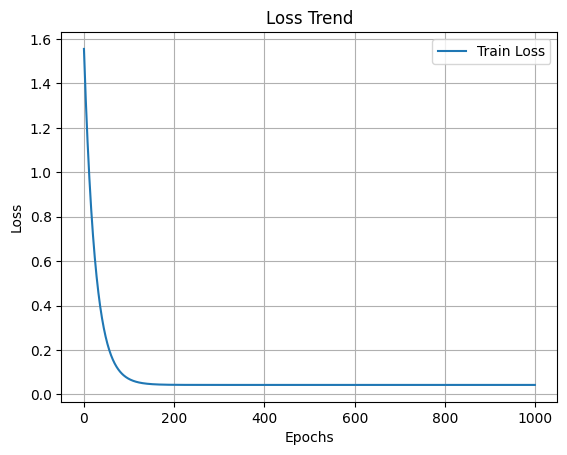

테스트

학습된 모델을 통해 테스트 데이터의 결과 예측

import numpy as np

def predict_test_data(test_data):
    # 테스트 데이터 표준화
    test_scaled = scaler_x.transform(test_data.reshape(-1, 1))
    test_tensor = torch.tensor(test_scaled, dtype=torch.float32).view(-1, 1).to(device)

    # 모델을 사용하여 예측
    model.eval()  # 평가 모드로 전환
    with torch.no_grad():
        predictions_scaled = model(test_tensor)

    # 표준화 해제
    predictions = scaler_t.inverse_transform(predictions_scaled.cpu().numpy())
    return predictions

# 예측할 테스트 데이터
test_years_experience = np.array([1.0, 2.0, 7.0])  # 1년, 2년, 7년의 경력을 가진  데이터를 사용
predicted_salaries = predict_test_data(test_years_experience)

# 결과 출력
for YearsExperience, salary in zip(test_years_experience, predicted_salaries):
    print(f'YearsExperience: {YearsExperience}, Predicted Salary: {salary[0]:.0f}')

YearsExperience: 1.0, Predicted Salary: 34298
YearsExperience: 2.0, Predicted Salary: 43748
YearsExperience: 7.0, Predicted Salary: 90998

결론

선형 회귀는 데이터 분석과 예측 모델링의 기초로서, 다양한 분야에서 널리 활용되고 있다.

본 포스팅을 통해 데이터 전처리, 모델 학습, 손실 함수 및 경사 하강법의 개념을 이해하고, 실제로 모델을 구현하는 과정까지 경험하였다.

이러한 지식은 단순한 선형 회귀 모델을 넘어, 다중 선형 회귀 모델 등 더 복잡한 머신러닝 기법으로 나아가는 토대를 마련해 줄 것이다.

profile
AAiss
.
이전 포스트

Supervised Learning

다음 포스트

Binary Classification

0개의 댓글