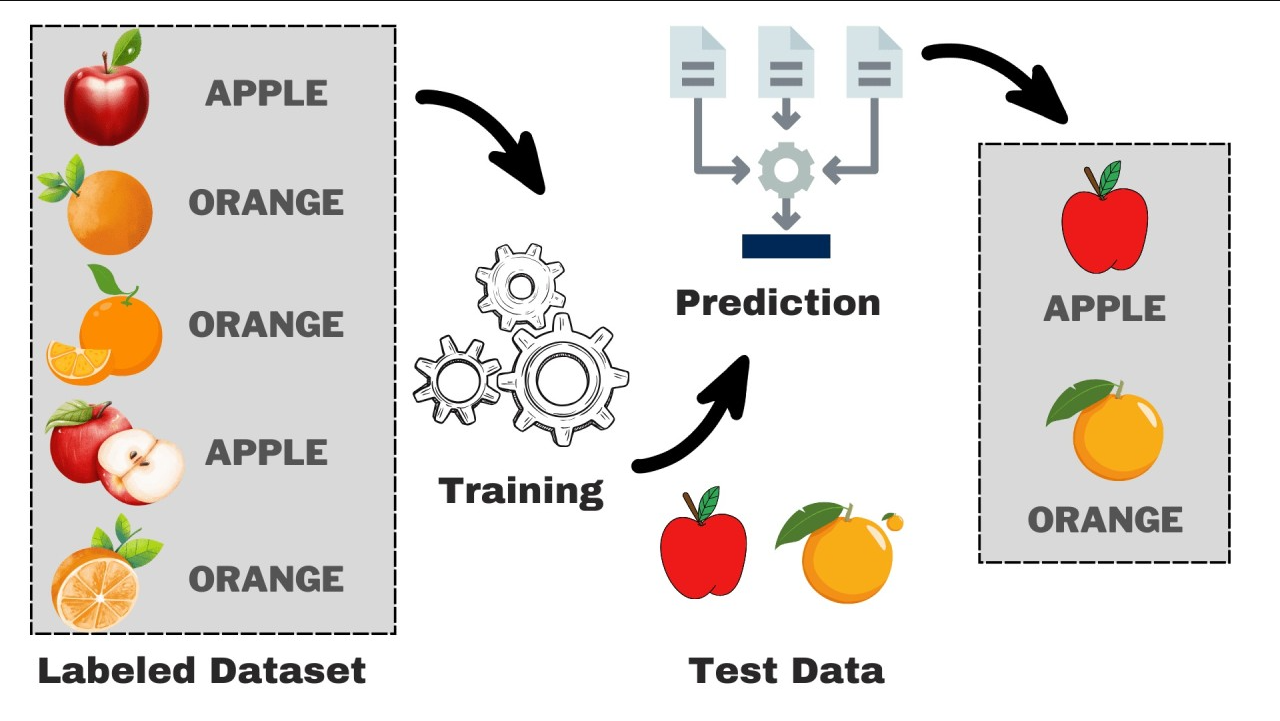
Supervised Learning

출처: https://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.kdnuggets.com%2Funderstanding-supervised-learning-theory-and-overview&psig=AOvVaw34FHZ4IWwtPShgE

입력 데이터(x)와 그에 대한 정답(y)를 이용해서 모델을 학습시키고 예측을 만드는 것

---

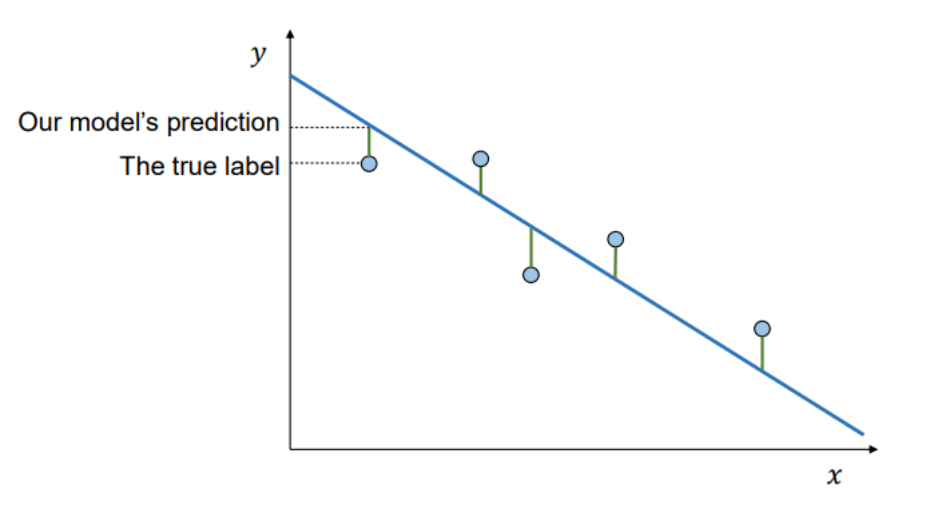
Cost Function

• 모델의 예측이 얼마나 잘못되었는지를 수치로 표현한 함수
• 즉, 정답(label)과 예측(prediction) 사이의 오차를 정량화함
• Loss function 또는 Objective function이라고도 불림
• 모델이 학습을 통해 오차를 줄이는 방향으로 파라미터를 조정할 수 있게 해 줌
• 비용이 높을수록 성능이 나쁜 모델이라는 뜻

Cost Function에 따라 학습 속도, 최종 정확도 등 학습 결과가 크게 달라질 수 있음

• Mean Absolute Error (MAE)
• Mean Squared Error (MSE)
• Cross-Entropy
• Hinge Loss
• Kullback-Leibler Divergence (KL-Divergence)

이외에도 다양한 Cost Function 존재

---

Linear Regression

• 독립 변수 𝑥와 종속 변수 𝑦사이의 선형 관계를 모델링하는 기법
• $𝑥=$ {$𝑥_1,$ $𝑥_2,$$...,$ $𝑥_𝑛$}, $𝑥_𝑖∈𝑅^𝑑$
• $y=$ {$y_1,$ $y_2,$$...,$ $y_𝑛$}, $y_𝑖∈𝑅$
• $a=$ {$a_1,$ $a_2,$$...,$ $a_𝑛$}, $a_𝑖∈𝑅$,     a: parameter
  
  
• $y=a_0+a_1x_1+a_2x_2+⋯+a_dx_d = \sum_{i=1}^d a_ix_i+a_0$

---

MSE

$C(x)= \frac{1}{n} \sum_{i=1}^n ∥y_i −y_i'∥^2 = \frac{1}{n} \sum_{i=1}^n∥y_i −f(x)∥^2$

---

MAE

$C(x)= \frac{1}{n} \sum_{i=1}^n ∥y_i −y_i'∥ = \frac{1}{n} \sum_{i=1}^n∥y_i −f(x)∥$

---

Training

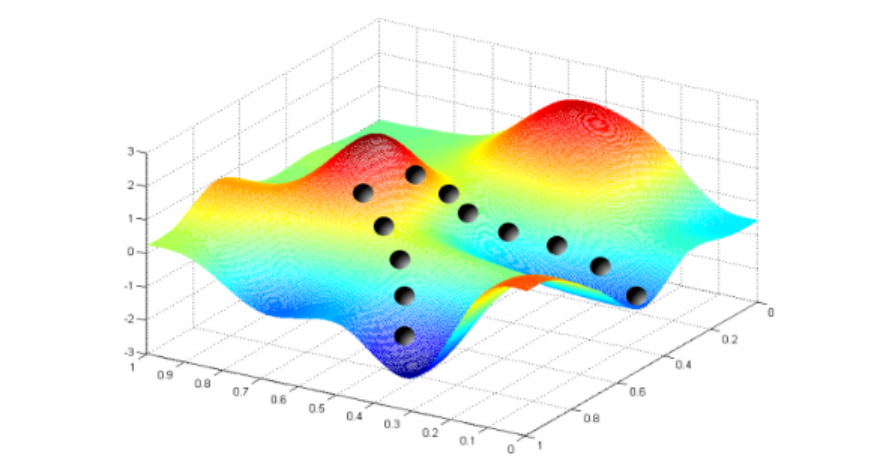
• 파라미터 $a_0,$ $a_1,$$...$를 조정하여 비용 함수 $C(a, x)$를 최소화하는 과정
• 대부분의 경우, 파라미터 공간(parameter space)은 매우 크고 복잡함
  • GPT-3는 약 1750억 개의 파라미터를 가짐
  • 조합의 수는 사실상 무한대에 가까움
• 학습은 무작위 초기값에서 시작하여 비용을 줄이는 방향으로 파라미터를 업데이트함
• 다양한 지역 최소점(local minima)이 존재
• 전역 최소점(global minimum)에 도달하는 것이 목표
  
  
  $Given a function$  $f:A→R,$ $find$   $x'∈A such that f(x')≤f(x),$ $∀x∈A$

• Gradient Descent (GD)
• Stochastic Gradient Descent (SGD)
• Gradient Descent with Momentum (Momentum)
• Adaptive Gradient Algorithm (AdaGrad)
• Adaptive Moment Estimation (Adam)
• Newton's methods
• Quasi-Newton (BFGS)

이외에도 다양한 알고리즘 존재

---

Gradient Descent

$\frac{dC(w)}{dw}= \frac{1}{n} X(Xw−y),$      $\frac{2}{n}$가 맞는 표현이지만 step size($η$)를 통해 $\frac{1}{n}$로 대체

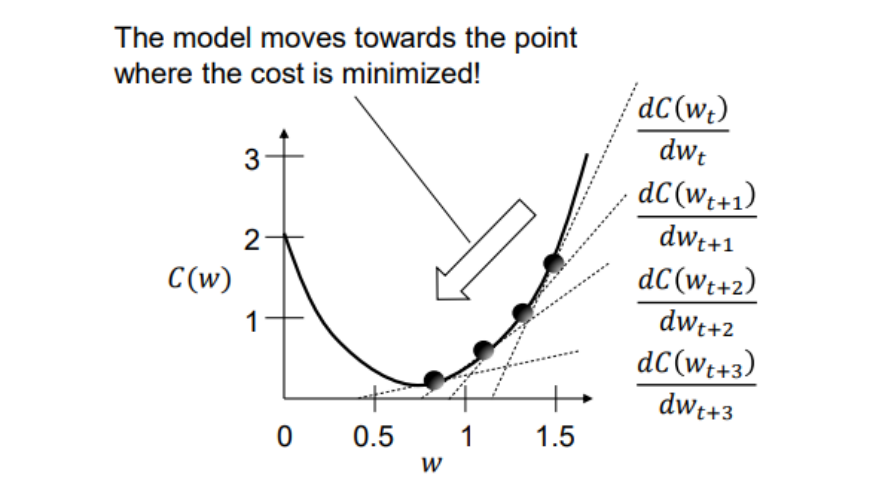
• 머신러닝, 신호처리, 통계학 등 다양한 분야에서 널리 사용되는 최적화 알고리즘
• 비용 함수(cost function)를 최소화하기 위해 파라미터를 점진적으로 업데이트
• 손실 함수의 수렴(convergence)을 보장(guarantee)
• 특히, 볼록 함수(convex function)의 경우 전역 최적해(Global minimum)에 도달 가능

---

Learning Rate (Step Size)

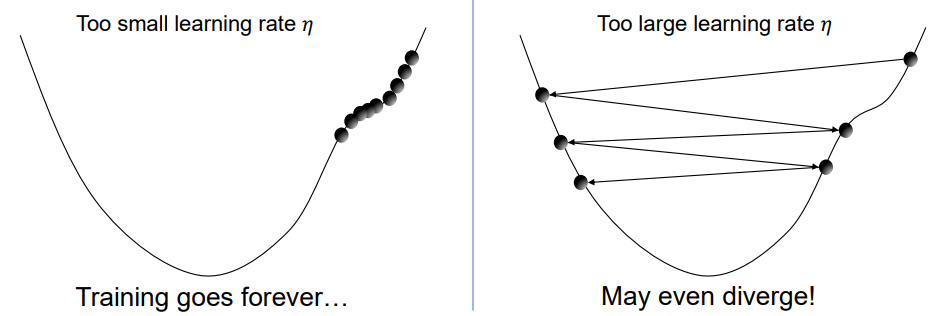
• 학습률 $η$는 경사 하강법에서 파라미터를 얼마나 업데이트할지를 결정하는 요소
• 일반적으로는 학습률 스케줄링 또는 적응형 옵티마이저(예: Adam)를 활용

---

Closed From Solutuion

$C(w)= \frac{1}{n}​ (Xw−y)^⊤ (Xw−y) ∝w^⊤ X^⊤Xw−2w^⊤ X^⊤ y+y^⊤y$


$\frac{dC(w)}{dw} = \frac{d}{dw}(w^⊤ X^⊤ Xw−2w^⊤ X^⊤ y+y^⊤y) = 0$
$\Leftrightarrow 2X^⊤Xw−2X^⊤y = 0 \Leftrightarrow X^⊤Xw=X^⊤y$


$w = (X^⊤X)^{-1}X^⊤y$

• 수학적으로 정확한 해를 계산
• $(X^⊤X)$가 비가역행렬이라면 의사역행렬(pseudo-inverse) 사용
• 시간 복잡도가 $O(n^3)$이기에 고차원 데이터에 적용 어려움

반면, GD는 $(X^⊤X)$를 직접 계산하지 않기에 고차원 데이터에 적용 가능
$𝑋∈𝑅^{𝑛×𝑑},$ $W∈𝑅^{d×1}$이므로 미분의 시간복잡도는 $O(nd)$

---

Logistic Regression

• 분류 문제를 위한 확률 기반 모델
• Sigmoid 함수를 사용해서 출력을 스쿼싱(squashing)함

• $f(x)=σ(w^⊤x)= \frac{1}{1+e^{−w^⊤x}}$
• $p(y=1∣x;w)≈f(x)$
• $p(y=0∣x;w)≈1-f(x)$
  
  
• $f(x) \geq 0.5 \rightarrow y = 1$
• $f(x) < 0.5 \rightarrow y = 0$

$f(x) = \frac{1}{1+e^{−w^⊤x}}$는 non-convex
이를 해결하기 위해 Maximum Likelihood Estimation 도입

---

Maximum Likelihood Estimation (MLE)

$w_{MLE} =argmax_w \sum_{i=1}^{n}log$ $p(y^i ∣x^i ;w)$

= $argmax_w \sum_{i=1}^{n}log$ $(p(y^i = 1 ∣x^i ;w)^{y^i} \cdot (1 - p(y^i = 1 ∣x^i ;w)^{1 - y^i}))$

= $argmax_w \sum_{i=1}^{n}[y^ilog$ $p(y^i = 1 ∣x^i ;w) \cdot (1 - y^i)log(1 - p(y^i = 1 ∣x^i ;w))]$
(Probability mass function of a Bernoulli distribution)

$C(w) = -\sum_{i=1}^{n}[y^ilog$ $f(x^i) \cdot (1 - y^i)log(1 - f(x^i))]$
(Binary Cross Entropy)

$\frac{dC(w)}{dw} = \frac{1}{n}\sum_{i=1}^{n}[(f(x^i) - y^i)x^i]$  
(MSE Cost Function의 미분 결과와 유사)

계산의 편의를 위해 상수는 고려하지 않음
이후, GD를 통해 파라미터 업데이트

---

Muiti-Class Logistic Regression

• $f(x)=σ(w^⊤x)= \frac{exp({w_c}^⊤x)}{\sum_{c=1}^{C}exp({w_c}^⊤x)}$
  
  
• $p(y=c∣x;w_1, w_2, ... , w_c)≈f(x)$
  
  
• $C(w) = -\sum_{i=1}^{n}\sum_{c=1}^{C}y_c^ilog$ $f_c(x^i)$
  
  
• $\frac{∂C(w)}{∂w_c}= \frac{1}{n}\sum_{i=1}^{n}(f_c(x^i )−y_c^i)x^i$

---

Decision Tree

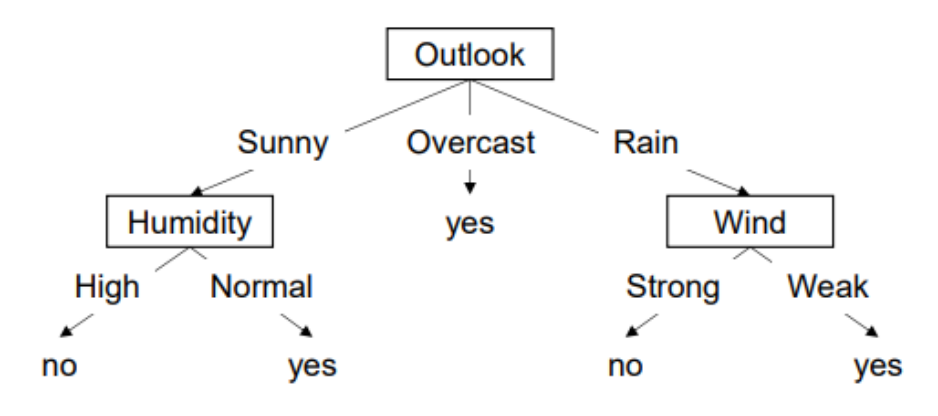
• 데이터로부터 의사 결정 규칙(decision rules)을 학습하여 예측 수행
• Non-parametric, supervised learning
• 분류(Classification)와 회귀(Regression) 모두에 사용 가능
• Feature scaling 불필요

• Internal Node: 특정 속성(변수)을 테스트하는 노드
  • ex) Humidity, Wind
    
    
• Branch: 테스트 결과(속성 값)에 따른 경로
  • ex) Humidity = High
    
    
• Leaf Node: 최종 예측값
  • ex) yes / no 또는, $p(y|x∈leaf)$

---

Algorithm

• CART (Classification and Regression Trees)
• ID3 (Iterative Dichotomister 3)
• C4.5
• CHAID (Chi-squared Automatic Interaction Detection)

ID3에 대해 다룰 예정

---

Iterative Dichotomister 3 (ID3)

• 결정 트리를 구성하는 탑다운(top-down) 방식의 탐욕적(greedy) 알고리즘
• 각 단계에서 가장 Information Gain이 큰 속성을 선택해 트리를 분할
• 순도 높은 집합으로 분리하므로, 더 적은 깊이로 leaf에 도달하는 구조를 유도

---

Entropy (Impurity)

• 랜덤 변수 𝑥의 정보량(uncertainty, 불확실성)의 평균
• $H(x)=− \sum_{i=1}^{n}p(x=i)log_2p(x=i)$

정보 이론에서는 정보의 불확실성이나 무질서도를 측정하는 지표
최적 부호화를 위해 필요한 평균 비트 수를 의미
평균 부호 길이: $\sum_{i=1}^{n}p(x=i) −log_2 p(x=i)$
자연계는 엔트로피가 높음

---

Information Gain (IG)

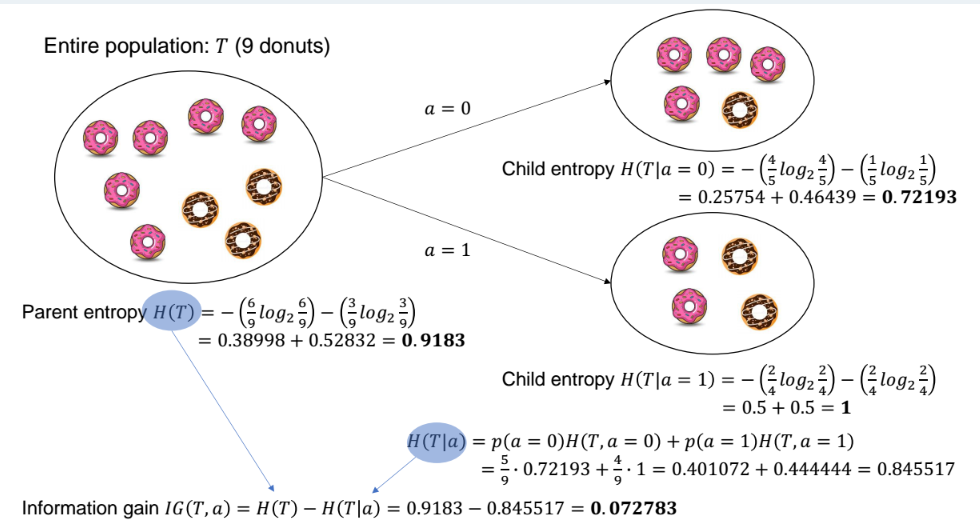
• 데이터를 어떤 feature로 분할했을 때 Entropy가 얼마나 줄어드는지를 측정
• $IG(T,a)=H(T)−H(T∣a)$
• $H(T|a)=\sum_{v∈values(a)} p(a=v)⋅H(Sa(v))$
• $S_a(v) =$ {$x∈T|x_a = v$}

장점

• 자동적이며 체계적인 노드 분할이 가능
• 모든 노드에서 엔트로피를 최소화하는 방향으로 트리를 구성

단점

• 많은 고유값을 가지는 속성에 의존 -> Fat Tree
  • ex) 고객 패턴 분류 시, 수많은 고유값을 가진 고객 ID를 기준으로 분할
  • 고유값이 많다고 해서 유익한 정보라고 보장할 수 없음

이를 개선하기 위해 Infromation Gain Ratio (IGR) 도입

---

Information Gain Ratio (IGR)

• IG를 각 속성의 분할 정보(Split Information)로 정규화함으로써 공정성을 확보
• $IGR(T,a)=\frac{IG(T,a)}{SplitInfo(T,a)}$
• $SplitInfo(T,a)=-\sum_{v∈values(a)}\frac{|T_v|}{|T|}log_2\frac{|T_v|}{|T|}$

$SplitInfo(T,a)=-(\frac{5}{9}log_2\frac{5}{9} + \frac{4}{9}log_2\frac{4}{9})=0.99085$
$IGR(T,a)=\frac{IG(T,a)}{SplitInfo(T,a)}=\frac{0.072783}{0.99085} ≈0.07345$

---

Overfitting

• 모델이 학습 데이터에는 정확히 맞추지만, 새로운 데이터에는 잘 일반화하지 못하는 현상
• 결과적으로 training accuracy는 높지만, validation accuracy는 낮음

• Training data: $error_{train}(h)$
• Entire distribution D of data: $error_D(h)$
• $error_{train}(h)<error_{train}(h')$ $and$ $error_D(h)>error_D(h')$

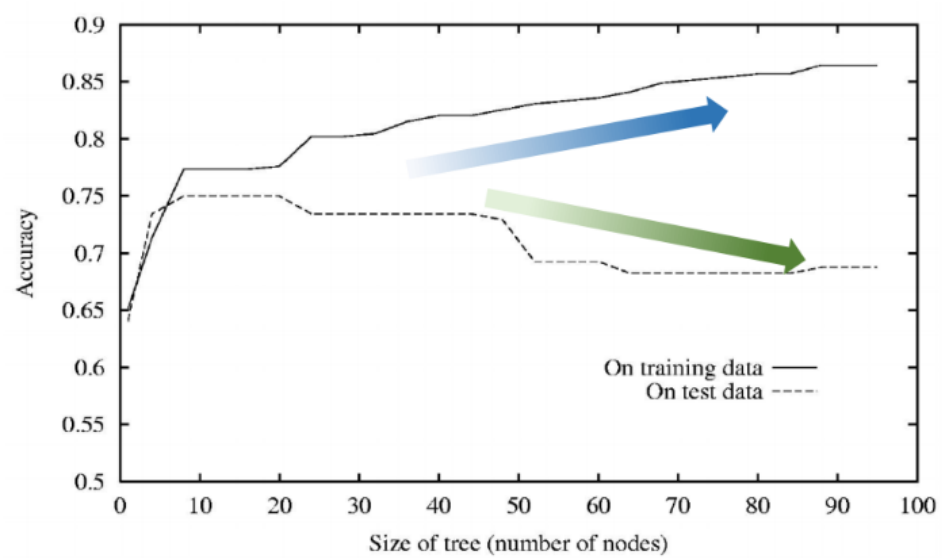
발생 원인

• 훈련 데이터 양이 부족하거나, 데이터가 전체 분포를 충분히 대표하지 못함
• 노이즈가 많은 데이터가 포함되어 있음 → 모델이 의미 없는 패턴까지 학습
• 특정 데이터셋에 대해 너무 오랫동안 학습
• 모델의 복잡도가 너무 높음 → 노이즈까지 학습함

해결 방법

• 더 많은 양질의 데이터 수집
• 데이터 정제
• 모델이 훈련 데이터에 완벽하게 맞추기 전에 학습을 멈추기
• 학습 후 가지치기(pruning)를 수행
  • Reduced-Error Pruning: 검증 데이터 기준으로 가지 제거
  • Rule Post-Pruning: 생성된 규칙을 간단히 다듬는 방식

---

Reduced-Error Pruning

1. 데이터를 훈련셋과 검증셋으로 분리
2. 훈련 데이터를 이용해 전체 트리 생성
3. 트리를 아래에서 위로(bottom-up) 탐색하면서
   • 각 노드를 제거해보고
   • 제거 후의 검증 정확도를 측정
   • 정확도가 유지되거나 향상된다면 해당 노드를 제거

이 경우 Humidity 노드를 제거하고 leaf 노드(negative)로 대체하면 4 corrects and 2 wrongs
즉, Humidity 노드를 제거함으로써 검증 정확도 향상

---

Why Might Predictions be Wrong?

True Non-determinism (비결정성)

• 동전을 던지면 결과는 확률적임
• $p(heads) = θ$라는 확률을 모델이 추정
• 머신러닝은 관측값으로부터 학습한 뒤, 기대값 측면에서 최선을 다하길 바라는 것
  
  

Partial Observability (부분 관측성)

• 예측에 필요한 정보가 관측된 x에 포함되어 있지 않거나 일부만 포함될 수 있음
  
  

Representational Bias (표현 편향)

• 적절한 특징(x) 선택이 중요
• 현재 특징만으로는 분리가 어려울 수 있음

---

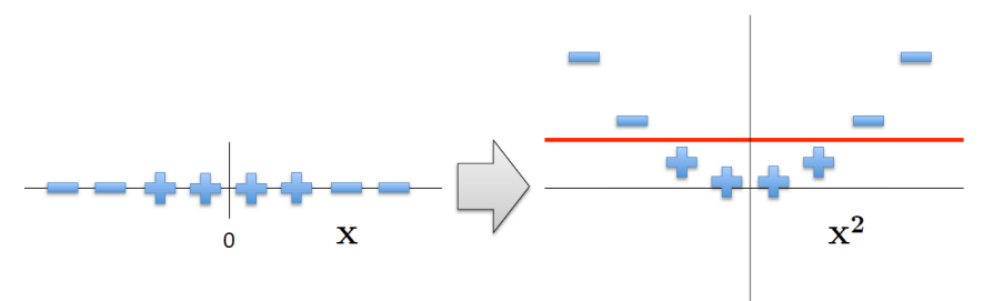
SVM (Support Vector Machine)

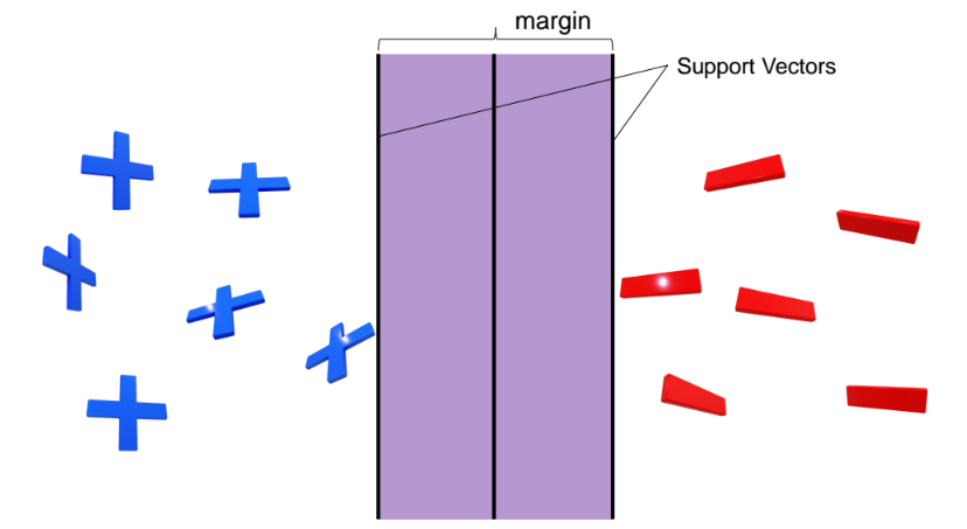
• 고차원 공간에서 데이터 포인트들을 명확히 분류하는 초평면(hyperplane) 을 찾는 것
• 두 클래스 사이의 margin(마진) 을 최대화(maximize)
• 즉, 각 클래스와 결정 경계 간의 최소 거리를 가장 크게 만드는 것이 목표

장점

• Versatile
  • 분류(classification)와 회귀(regression) 문제 모두에 사용 가능
    
    
• Linearity
  • 커널 트릭(Kernel Trick)을 통해 비선형 문제도 선형적으로 다룰 수 있음
    
    
• Well-Studied
  • 수학적으로 잘 연구되어 있고 이해가 쉬움
    
    
• Robust
  • 데이터가 적거나 노이즈가 많아도 상대적으로 좋은 성능을 보임

---

Decision Rules

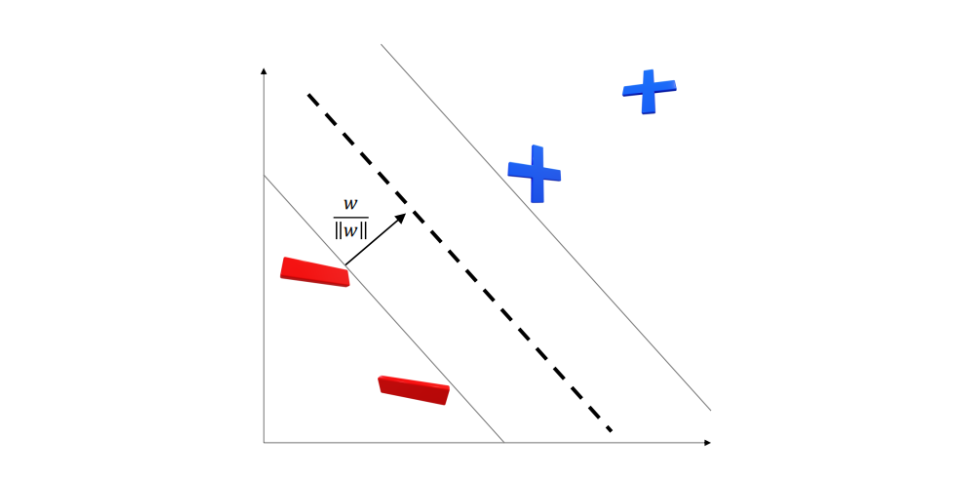
• $y_i(w⋅x_i +b)≥1,$  $y_i∈$ {$-1, 1$}
• $width = \frac{2}{||w||} \rightarrow min\frac{1}{2}||w||^2,$ $Subject$ $to$ $y_i(w⋅x_i +b)-1\geq0,$ $i = 1, 2, ... , n$

• $L(w,b,α)= \frac{||w||^2}{2} − \sum_{i=1}^{n}α_i(y_i(w^Tx_i +b)−1)$
• $Subject$ $to$ $\alpha_i\geq0,$ $i = 1, 2, ..., n$
• $min_{w,b}L(w, b, a)$

이후 Lagrangian Primal-Dual을 통해 최적의 $\alpha_i$ 도출
$w = \sum\alpha_iy_ix_i$, 이를 $y_i(w⋅x_i +b)-1=0$에 대입하여 $b$ 도출
이렇게 도출된 $w$와 $b$는 마진의 최대화를 보장

---

Complementary Slackness Condition

$\alpha_i(y_i(w⋅x_i +b)-1=0),$ $\alpha_i\ge0$

• Support Vector
  • $y_i(w⋅x_i +b)-1=0$
  • $\alpha_i \neq 0$
  • 경계에 위치한 점
    
    
• Internal Point
  • $y_i(w⋅x_i +b)-1\neq0$
  • $\alpha_i = 0$
  • 여유 있게 잘 분류된 점

---

Kernel Method

• 커널 함수는 어떤 고차원 feature space에서의 inner product를 의미
• 어떤 함수가 symmetric하고 positive semi-definite이면 유효한 커널 함수
• $K(x_i ,x_j)=ϕ(x_i)^T ϕ(x_j)=x_i^TA^TAx_j$

• $K(u, v) = (u\cdot v)^d$
• $K(u, v) = (u\cdot v + 1)^d$
• $K(u, v) = tanh(u\cdot v + 1)^d$
• $K(u, v) = exp(-\frac{||u-v||^2}{2σ^2})$

---

Kernel Trick

고차원 맵핑을 하지 않아도 마치 고차원 공간에서 작동하는 것처럼 구현 가능

$K(x_i, x_j) = <x_i, x_j>^2 = (x_{i1}x_{j1}+x_{i2}x_{j2})^2 = (x_{i1}^2 x_{j1}^2 + x_{i2}^2 x_{j2}^2 + 2x_{i1}x_{i2}x_{j1}x_{j2})$

$=$ $<\Phi(x_i), \Phi(x_j)>,$ $\Phi(x_i)=(x_{i1}^2, x_{i2}^2, \surd{2} x_{i1}x_{i2}),$ $\Phi(x_j)=(x_{j1}^2, x_{j2}^2, \surd{2} x_{j1}x_{j2})$

---

Soft-Margin SVM

$min\frac{1}{2}||w||^2 + C\sum_{i=1}^{n}ξ_i,$ $Subject$ $to$ $y_i(w⋅x_i +b)-1\geq0,$ $i = 1, 2, ... , n$

Complementary Slackness Condition

$\alpha_i(y_i(w⋅x_i +b)-1+ξ_i=0),$ $\alpha_i=C-γ_i,$ $γ_iξ_i=0$

• Support Vector
  • $y_i(w⋅x_i +b)-1=0$
  • $0<\alpha_i<C,$ $γ_i>0,$ $ξ_i=0$
  • 경계에 위치한 점
    
    
• Internal Point
  • $y_i(w⋅x_i +b)-1\neq0$
  • $\alpha_i=0,$ $γ_i=C,$ $ξ_i=0$
  • 여유 있게 잘 분류된 점
    
    
• Beyond Margin
  • $\alpha_i(y_i(w⋅x_i +b)-1+ξ_i)\neq0$
  • $\alpha_i=C,$ $γ_i=0,$ $ξ_i>0$
  • 마진을 침범한 데이터(오분류)

---