RNN
1. BackGround
1) Sequential Data
앞서 보았던 딥러닝 모델들은 크기가 정해져있는 데이터들을 다루는 모델이었다.
하지만, 실생활에서 접할 수 있는 데이터의 대부분은 시계열 데이터로, 그 크기가 정해져 있지 않고 시간순서 또한 고려해야 하는 데이터들이다.
예를 들어, 주식 가격을 생각해 보자.
과거의 데이터를 활용해 미래의 주가를 예측해본다고 할 때, 시간순서대로 데이터를 학습해야 할 것이다.
2) 과거의 모델
이 문제를 해결하기 위해 과거에는 아래와 같이 주로 통계학이나 확률과 같이 수학적으로 접근했었다.
- Naive Sequence Model
- Autoregressive Model
- Markov Model
해당 모델들은 우리의 예측에 대한수학적 근거를 제시해 주지만 모든 경우에 대한 확률을 알아야 하기 때문에 정확한 예측이 힘들다는 단점이 있었다.
2. Vanilla RNN
1) Idea
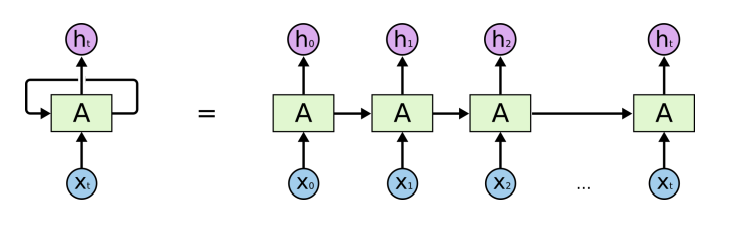
Sequential Data를 처리하기 위해서는 미래의 예측에 과거의 정보를 반영해야 한다.
즉, 과거의 정보를 함축해서 담고 있을 공간이 필요하다는 것이다.
Vanilla RNN에서는 과거의 정보를 Hidden Cell이라는 공간에 과거의 정보를 저장하고 있다가,
현재의 Input이 들어올 경우 이 두 정보를 동시에 고려해 예측값을 구하도록 구현해 주었다.
2) BPTT
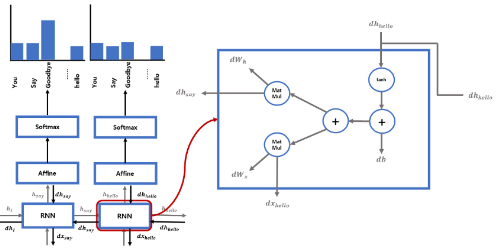
RNN에서의 BackPropagation방법은 일반적인 방법과 다르게 동작한다.
이 방법을 BPTT(BackPropagation Through Time)라고 한다.
우리는 이 BPTT를 통해 RNN을 기반으로 하는 모델들의 학습이 가능하다.
해당 내용 학습시 다음 블로그 참조
3) 특징
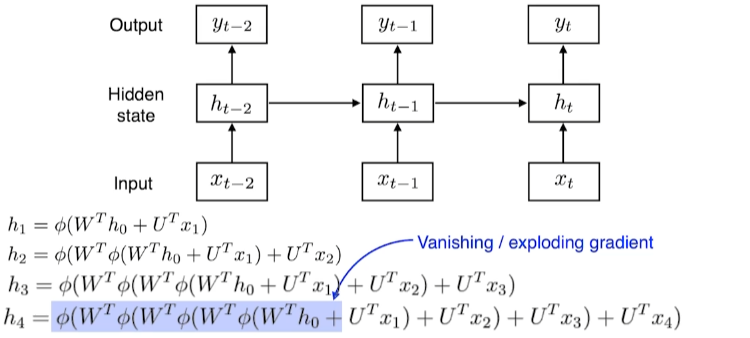
입력이 길어질 때, 과거의 정보는 계속 연산의 대상이 되기 때문에 결국 미래에는 사라지거나 너무 커지게 된다.
예를 들어 활성화 함수로 Sigmoid나 tanh를 사용한다고 하면 입력이 길어지면 처음 입력되었던 정보는 점점 작아진다.
반면에 활성화 함수로 ReLU를 사용한다고 할 때, 입력이 길어지면 처음 입력했던 정보의 크기는 계속 커지게될 것이다.
2. LSTM
1) Idea
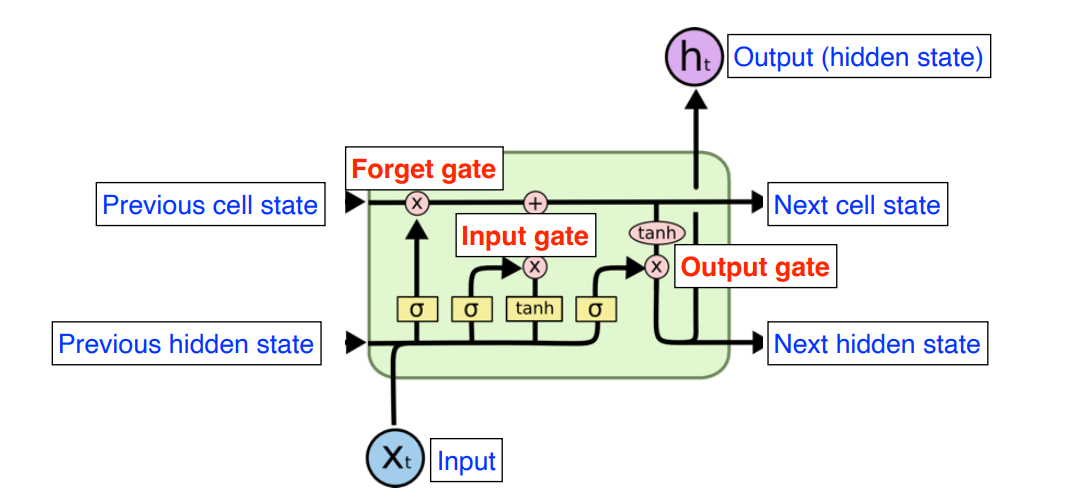
먼저 있었던 RNN은 Data의 길이가 길어질수록 Vanishing, Exploding Gradient에 의해 과거의 정보를 보존할 수 없다는 단점을 가지고 있었다.
이를 해결하기 위해 LSTM은 Gate의 개념을 도입하였는데, Forget Gate를 통해 Exploding Gradient를, Input gate와 Cell State를 통해 Vanishing Gradient를 방지해 주었다.
2) 동작과정
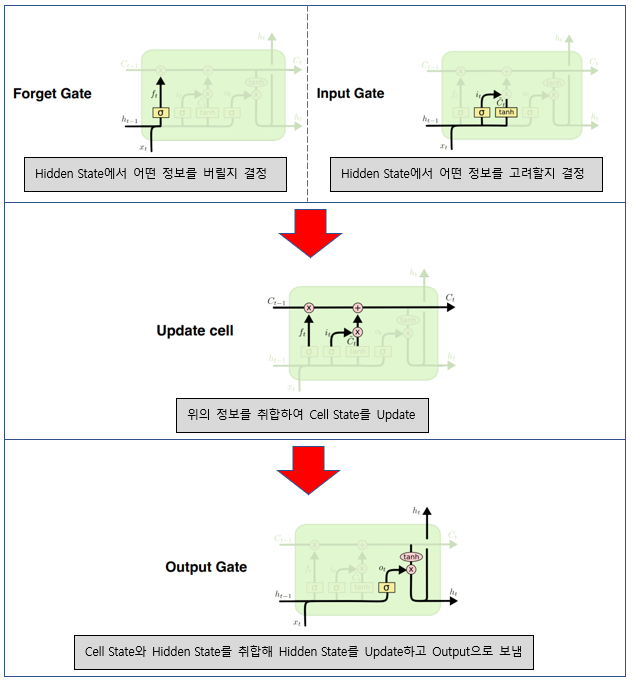
내부가 RNN에 비해 많이 복잡해 졌지만 동작 과정을 천천히 살펴보면 위와 같다.
- Gate를 통해 과거의 내용 중 버릴 정보와 기억할 정보를 골라낸다.
- 해당 정보를 Cell State에 Update한다.
- 현재의 정보와 Cell State를 합친다.
- 위에서 합친 정보를 다음 LSTMCell에 넘겨줌과 동시에 Output으로 내보낸다.
3) 특징
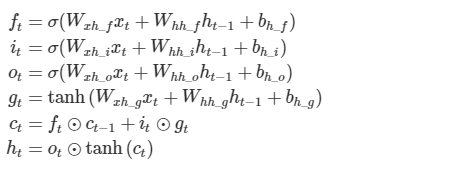
위의 과정을 잘 살펴 보면 Cell State를 두번 Update하게 되어 불필요한 과정이 생긴 것 같음을 느낄 수 있다.
즉, 불필요한 연산과 Parameter들로 인해 예측 시간과 성능이 떨어질 수 있다는 것이다.
(Parameter의 수가 많아질 수록 Generalization성능이 떨어진다는 것은 앞서 설명했다.)
3. GRU
1) Idea
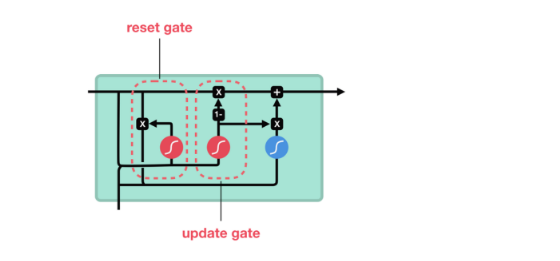
LSTM은 그 복잡한 구조 때문에 RNN에 비해 많은 파라미터가 필요하게 되었다.
GRU는 이 점을 해결하기 위해 제안되었는데 이 아이디어의 핵심은 Reset Gate와 Update Gate만을 활용해 LSTM의 Forget, Input, Output을 모두 수행하는 것이다.
(여담으로, GRU를 만드신 교수님 중 한분이 우리나라의 조경현 교수님이라고 한다.)
2) 동작 과정
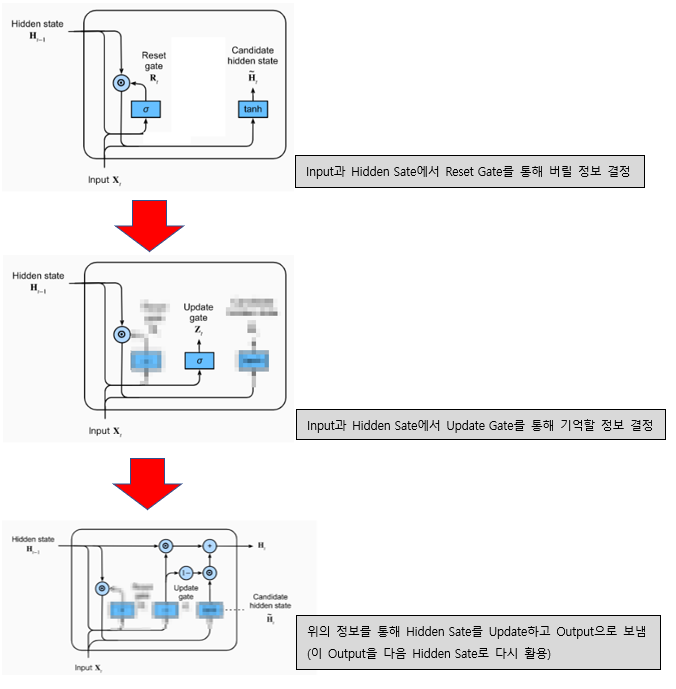
동작 과정을 살펴보면 LSTM에 비해 훨씬 간단해 졌다는 것을 확인할 수 있고, 필요한 Gate의 수도 작아졌음을 눈으로 확안할 수 있다.
간단하게 살펴보면 다음과 같은 과정을 거친다.
- 버릴 정보와 기억할 정보를 설정한다.
- 위의 정보를 Hidden State에 Update한다.
- 이 Hidden State를 Output으로도 활용한다.
RNN - Pytorch 예제
1. Back Ground
1) 객체 생성
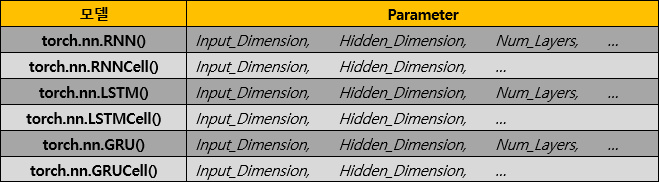
Pytorch에서는 기본적으로 완전히 구현된 RNN, LSTM, GRU모델을 Class로 제공한다.
즉, 해당 Class로 객체를 만들고 사용할 줄만 알면 간단하게 구현할 수 있다.
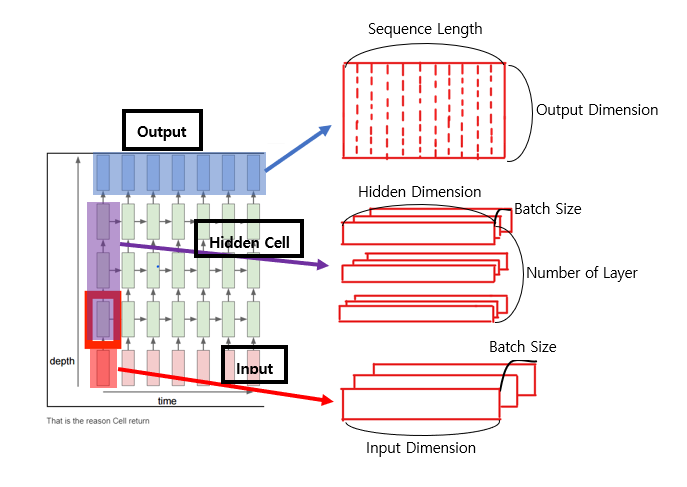
Parameter 설명
- Input_Dimension
: Input으로 들어오는 데이터의 Feature의 개수
(Input데이터의 길이가 아님을 유의하자)
- Hidden_Dimension
: Hidden Layer에서 사용할 Feature의 수
(Input데이터와 과거의 데이터를 합쳐 Hidden Layer에 저장할 때, 몇개의 Feature를 사용하고 싶은지)
- Num_Layer
: 사용할 Hidden Layer의 개수(아래 Input과 Output에서 그려놓은 그림을 참고하면 이해하기 쉬울 것이다.)
RNN Vs RNNCell
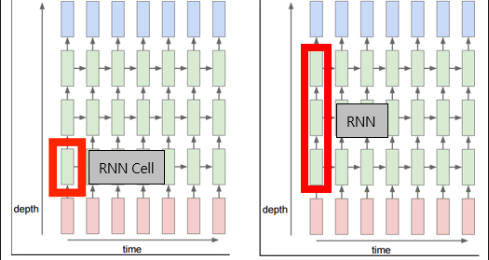
Pytorch에서는 Cell버전과 온전한 버전 두가지로 나누어 모델을 제공한다.
이때, Cell은 위의 표시와 같이 Hidden Layer가 1개인 객체를 만들어 주어, 사용자가 자유롭게 모델을 구성할 수 있도록 해준다.
반면에 그냥 RNN은 Num_Layers라는 Parameter를 따로 받아 내부적으로 정해진 방식대로 객체를 만들어 사용자에게 제공해 준다.
2) Input과 Output
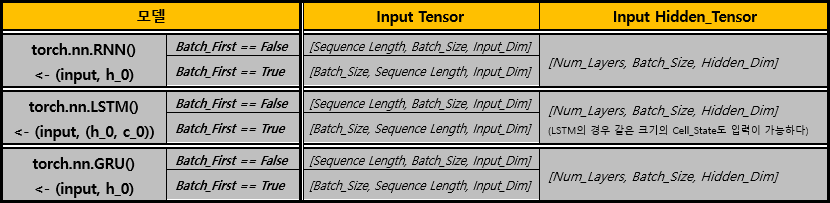

Input
rnn객체에 Input Data를 입력할 때에는 위의 형식을 지켜야 한다.
또한, Input과 같이 미리 Hidden Layer도 설정이 가능한데, 만약 해당 Tensor를 전달하지 않을 경우 Hidden Layer가 자동으로 0으로 채워지는 것 같다.
LSTM의 경우 c_0도 같이 입력이 가능하다.
Output
rnn객체에서 학습 결과를 받아올 때에는 위와 같은 형식으로 Return된다.
마찬가지로 추후에 사용할 수 있도록 Hidden Layer(LSTM의 경우 c_0)도 같이 출력되는 것 같다.
그림
그림으로 위의 과정들을 전체적으로 표현해 보면 다음과 같다.
(자세한 내용은 공식 문서를 참조)
2. 예시문제1
1) 방법1
먼저 RNN의 기본적인 IDEA를 가지고 처음부터 끝까지 구현해 보자.
import torch.nn as nn class RNN(nn.Module): def __init__(self, input_size, hidden_size, output_size): super(RNN, self).__init__() self.hidden_size = hidden_size self.i2h = nn.Linear(input_size + hidden_size, hidden_size) self.i2o = nn.Linear(input_size + hidden_size, output_size) self.softmax = nn.LogSoftmax(dim=1) # 이 경우 hidden cell을 반복적으로 입력받도록 구현해야 하므로 # hidden또한 return값에 포함해야 한다. def forward(self, input, hidden): combined = torch.cat((input, hidden), 1) hidden = self.i2h(combined) output = self.i2o(combined) output = self.softmax(output) return output, hidden def initHidden(self): return torch.zeros(1, self.hidden_size)
import torch.optim as optim n_hidden = 128 rnn = RNN(n_letters, n_hidden, n_categories) learning_rate = 0.005 criterion = nn.NLLLoss() optimizer = optim.SGD(rnn.parameters(), lr = learning_rate) def train(category_tensor, name_tensor): hidden = rnn.initHidden() rnn.zero_grad() for i in range(name_tensor.size()[0]): output, hidden = rnn(name_tensor[i], hidden) loss = criterion(output, category_tensor) # 학습 (w = w - learning_rate * gradient) optimizer.zero_grad() loss.backward() optimizer.step() return output, loss.item() ##### optimizer.step()의 경우 다음과 같이 사용할 수 있다.##### # # # loss.backward() # # for p in rnn.parameters(): # # p.data.add_(p.grad.data, alpha=-learning_rate) # # # #########################################################
2) 방법2
이 방법은 Pytorch library에 존재하는
nn.RNN을 이용해 방법1과 똑같이 작동하는 모델을 구현해 보는 방식이다.
# RNN모델 구현(2번 -> nn.RNN사용) import torch.nn as nn class RNN(nn.Module): def __init__(self, input_size, hidden_size, output_size, num_layers): super(RNN, self).__init__() self.hidden_size = hidden_size self.input_size = input_size self.num_layers = num_layers self.output_size = output_size self.rnn = nn.RNN(input_size, hidden_size, num_layers) self.fc = nn.Linear(hidden_size, output_size) def initHidden(self): return torch.zeros(self.num_layers, 1, self.hidden_size) def forward(self, input): hidden = self.initHidden() output, _ = self.rnn(input, hidden) output = output[-1] output = self.fc(output) output = nn.LogSoftmax(dim=1)(output) #output = output.reshape(-1) return output
import torch.optim as optim n_hidden = 128 # hidden의 출력층 크기 rnn = RNN(n_letters, n_hidden, n_categories, 2) learning_rate = 0.005 # learning rate criterion = nn.NLLLoss() # nn.LogSoftmax에 가장 적합한 손실함수 optimizer = optim.SGD(rnn.parameters(), lr = learning_rate) # Gradient Descent의 방법으로 SGD Optimzer 사용 def train(category_tensor, name_tensor): hidden = rnn.initHidden() rnn.zero_grad() output = rnn(name_tensor) loss = criterion(output, category_tensor) optimizer.zero_grad() loss.backward() # 학습 (w = w - learning_rate * gradient) optimizer.step() return output, loss.item()