딥러닝
3) Loss Function Select
우리는 위에서 정한 Hypothesis Model을 통해 구한 결과값 y와 우리가 원했던 값(정답값)의 차이를 구하고, 이것이 줄어들도록 하여 학습을 진행시키게 된다.
이를 위해선 우선 결과값
y와 우리가 원했던 값(정답값)t의 차이에 대한 정의를 할 필요가 있다.
가장 간단하게 생각할 수 있는 방법은 그냥 단순하게 두 값의 차이의 절대값으로 정의하는 것이다. 하지만 실제로는 이 방법보다 주로 다음의 방법을 사용한다.
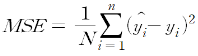
- MSE(Mean Squared Error)
: 두 값의 차이의 제곱의 평균
:0 < |y-t| < 1인 y에 대해서는 작은 차이를, 그 외의 y에 대해서는 큰 차이를 주어 학습의 속도를 빠르게 할 수 있다.
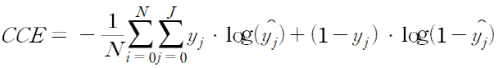
- CCE(Cross Entropy Error)
: KL Divergence(두 확률 분포의 차이)를 활용한 Error표현
: 정보이론에서 불확실성에 대한 척도를 의미하는 Entropy를 도입해 이 Entropy를 줄이는 방향으로 학습을 하는 방식이다.(Cross Entropy Error를 사용하기 전, 정답값에 대한 One Hot Encoding이 필요하다.)
(Cross Entropy Error는 주로 Classification문제에 대해 많이 사용된다)
- Hinge Loss
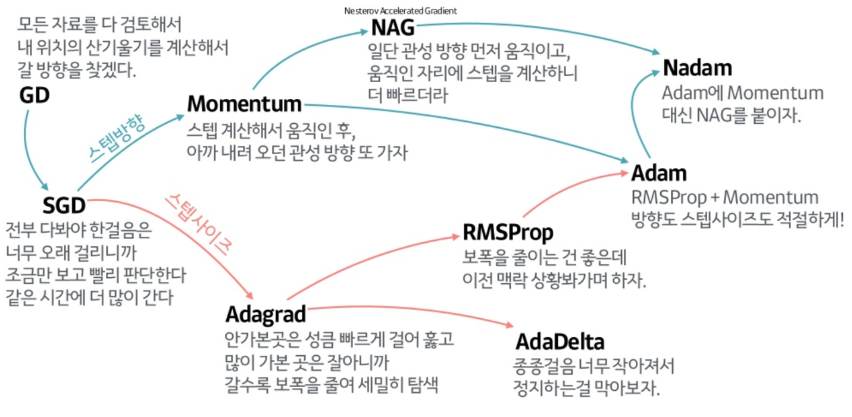
4) Optimization
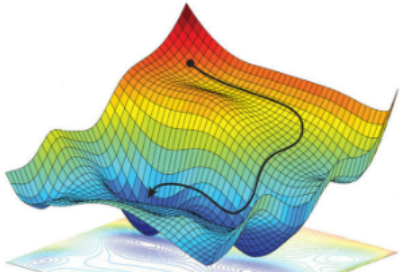
Gradient Descent(경사 하강법)
model의 Parameter를 조절해 Loss Function의 값을 줄이도록 하는 방법을 의미한다.
이를 위해서 벡터 미적분학에 존재하는 Gradient의 개념을 도입하게 된다.
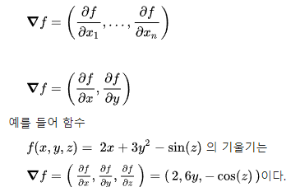
Gradient는 벡터 미적분학에서 함수(스칼라장)의 최대 증가율을 나타내는 벡터장을 의미한다.
즉, Gradient는 해당 지점에서의 최대 기울기와 그 방향을 나타낸다.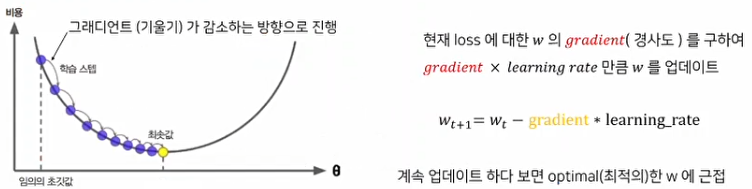
따라서 위와 같이 현재의 Parameter에서 이 Gradient를 빼주는 방식을 반복함으로써 Loss Function의 값을 0에 가깝게 만들 수 있다.
가장 기본적인 개념은 위와 같고, 추가적으로 어떤것을 고려해 주냐에 따라 여러 종류의 경사 하강법이 존재한다.
(참고: learning rate)
Gradient를 얼마만큼 변경해 줄 것인가에 관한것을 learning rate라고 한다. 이 때, 이 learning rate(학습률)의 변경률을 조절할 때, 다음과 같은 상황이 발생할 수 있으므로 주의해야 한다.
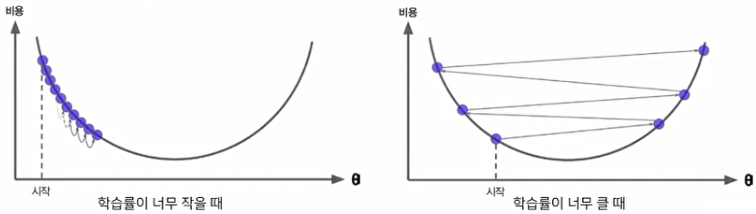
또, 이 learning rate는 어떤 종류의 Gradient Descent를 사용하는지에 따라 적절한 설정값이 다르기 때문에 이에 유의해야 한다.
(참고: Gradient descent의 종류)