알고리즘 - 6. Dynamic Programming

Ui Jin·2022년 2월 27일

DP 알고리즘

Algorithm

목록 보기

6/10

Dynamic Programming의 이해

다이나믹 프로그래밍이란 큰 문제를 작은 문제들로 나누어 풀고, 이 결과들을 저장해 두어 후에 큰 문제를 풀 때 이용하는 것을 의미한다.

이렇게 문제를 작은문제들로 나누어 풀 경우 다음과 같은 장점이 있게 된다.

큰 문제를 풀기 위해 비교적 쉬운 작은 문제부터 접근하기 때문에 쉽게 풀어나갈 수 있다.
한번 풀었던 작은 문제들은 다시 풀지 않아도 저장된 값을 활용할 수 있기 때문에 시간 단축이 가능하다.

위의 두 장점을 차근차근 이해해 보자.

우선, 첫번째 장점에 대한 예시로 제일 많이 설명되는 것이 피보나치 수열이다.

피보나치 수열은 다들 알다 싶이 Fibo[i] = Fibo[i-1] + Fibo[i-2]의 규칙을 가지는 수열이다.

1. 간단한 피보나치 수열

1) 코드
int Fibo(int n){
    if (n == 1)
        return 0;
    else if (n == 2)
        return 1;
    else
        return Fibo(n - 1) + Fibo(n - 2);
}
2) 전개 과정(그림)

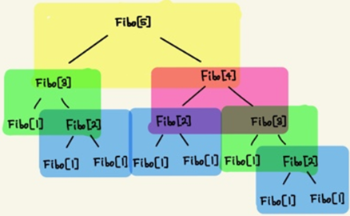
3) 설명

해당 코드에서Fibo[5]를 구하는 과정을 살펴보자.

먼저, Fibo[5]는 Fibo[3]과 Fibo[4]를 호출한다.

또 Fibo[4]는 Fibo[3]과 Fibo[2]를,Fibo[3]는 Fibo[2]과 Fibo[1]을 호출한다.

이 때 잘 생각해 보면 Fibo[5]를 구하기 위해 호출한 Fibo[3]이 있었음에도 불구하고 Fibo[4]를 구하기 위해 Fibo[3]를 다시 한번 구하게 된다.

즉, 다시 말해서, Fibo[i]를 구해야 할 때마다 계속 계산해야 한다는 것이다.

2. DP 피보나치 수열

1) 코드
(코드2)
int Fibo_Table[100];
int Fibo(int n) {
    if (n == 1) 
        return 1;
    if (n == 2) 
        return 1;
    if (Fibo_Table[n] != 0) 
        return Fibo_Table[n];
    return Fibo_Table[n] = Fibo(n - 1) + Fibo(n + 1);
}
2) 전개과정(그림)

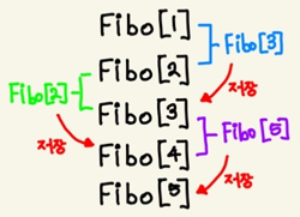
3) 설명

위의 과정을 간단한 피보나치 수열에서의 코드와 비교하여 생각해보자

먼저, Fibo[5]는 Fibo[3]과 Fibo[4]를 호출한다.

또 이와 마찬가지로 Fibo[4]는 Fibo[3]과 Fibo[2]를,
Fibo[3]는 Fibo[2]과 Fibo[1]을 호출한다.

이 때 잘 생각해 보면 Fibo[4]를 구하기 위해 Fibo[3]를 구했었고, 이를 Fibo_Table에 저장해 놓았기 때문에, Fibo[5]를 구하기 위해 호출한 Fibo[3]는 계산을 하지 않고 값을 가져오기만 하면 된다.

즉, 다시 말해서, 연산 시간을 훨씬 줄일 수 있게 된다.

3. DP의 의의

즉, Dynamic Programming의 가장 큰 의미는 Exponential Time Complexity를 갖는 알고리즘을 Polynomial Time Complexity를 갖도록 바꿔줄 수 있다는 것이다.

DP 적용과정

DP는 경우의 수, 최소값/최대값 을 구하는 문제를 최적화 할 때 사용할 수 있다.

-> 작은 경우 예시 생각
-> 우리가 비교해야 하는 값을 구한다.
-> 해당 값들이 더 작은 SubProblem으로 나누어 지는 지 생각해본다.
이 때 최적성의 원칙 생각.
즉, 우리가 쪼갠 여러개의 SubProblem들이 각각 최적의 해를 항상 포함하도록 해야함
-> 위의 과정을 일반화하여 dp Table을정의
-> dp Table의 의미 파악
-> dp Table을 채우는 방향 파악

DP 연습

1. String 편집 거리

두 String, Source와 Target의 유사도를 측정하는 알고리즘으로 삽입, 삭제 변환 연산을 사용해 S를 T로 변환하는데 드는 최소 연산 비용을 구하는 문제이다.

(참고: String 편집거리는 Levenshtein Distance라고도 한다.)

1) 아이디어

1. 부분 문제의 가능성 판단

예를 들어, 우리는 GU를 GAM으로 바꾸는데 필요한 최소 비용을 구해야 한다고 가정해보자.

이 때, 우리는 "삽입", "삭제", "변환" 이 3가지 연산만 사용할 수 있다. 결국 마지막에 3가지 연산중 하나를 사용하는 순간 GAM이 완성되는 것이다.

따라서 결과를 구하기 위해서는 이 3가지 경우만 비교해보면 되고, 이 과정은 다음과 같이 생각해 볼 수 있다.

삽입
: GA를 만들어 놓고 M을 삽입한다.

삭제
: Source에서 맨 뒤 글자만 빼고 GAM을 만들고 맨 뒤 글자를 삭제한다.

변환
: Source에서 맨 뒤 글자만 빼고 GA까지만 만들고, 맨 뒤 글자를 변환

즉, 잘 생각해보면 GU를 GAM으로 만들기 위해서는 좀 더 작은 문제의 정보가 필요하게 된다.

2. DP Table 정의

(참고)
: 위의 예시에서 생각해보면 맨 뒤의 글자가 같은 경우 굳이 변환할 필요가 없다.

2) 코드

DP Table의 의미

i-1->i인 경우는 삽입, j-1->j인 경우는 삭제, i-1->i and j-1->j인 경우는 변환 이라는 것을 확인할 수 있다.

DP Table을 채우는 방향

dp[i][j]를 구하기 위해서는 dp[i-1][j], dp[i][j-1], dp[i-1][j-1]이 먼저 구해져 있어야 한다.
즉 왼쪽에서 오른쪽, 위에서 아래로 DP Table을 채워야 한다
double dp[100][100];
int Levenshtein_Distance(string source, string target){
	double del=1, ins=1, exc=1;				// 각 비용 설정
	for(int i=0; i<=source.length(); i++)	// dp Table초기화
    	dp[0][i] = del*i;
    for(int i=0; i<=target.length(); i++)
    	dp[i][0] = ins*i;

    for(int i=1; i<=target.length(); i++) {	// dp Table 채워넣기
    	for(int j=1; j<=source.length(); j++) {
        	if(target[i]==source[j])
            	dp[i][j] = dp[i-1][j-1];
            else
            	dp[i][j] = dp[i-1][j-1] + exc;
            dp[i][j] = min(dp[i-1][j]+ins, dp[i][j-1]+del, dp[i][j]);
        }
    }
    return dp[source.length()][target.length()];
}
Time Complexity: O(NM)

(N은 Source문자열의 길이, M은 Target문자열의 길이)

2. 연쇄 행렬 곱셈

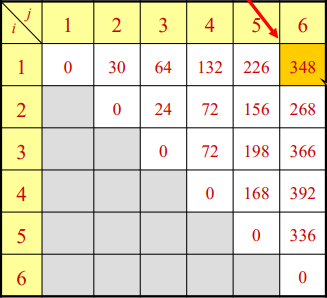
N개의 행렬을 구해야 한다고 할때, 이 행렬의 곱셈순서에 따라 컴퓨터가 수행하는 총 연산의 횟수가 달라진다. 이때, 이 연산 횟수의 최솟값을 구하는 문제이다.

예를들어 A1(10*100)행렬, A2(100*5)행렬, A3(5*50)행렬을 곱한다고 할 때,
(A1 * A2) * A3의 순서로 계산할 경우 7500번의 연산이 발생하고
A1 * (A2 * A3)의 순서로 계산할 경우 75000번의 연산이 발생한다.

(참고: 행렬곱 알고리즘은 보통 O(n^3)의 복잡도를 가지는데, 슈트라센 알고리즘을 사용하면 O(n^2.3)까지 줄일 수 있다.)

1) 아이디어

우선 가장 간단한 방법인 가능한 모든 순서를 고려해 보는 방법을 생각해보자. 이 경우, O(2^n)의 Exponential Time이 걸린다. 즉, Time Complexity를 줄일 수 있는 새로운 방법을 생각해 보아야 한다.

1. 부분 문제의 가능성 판단

5개의 행렬 A1, A2, A3, A4, A5를 곱하는 경우를 생각해 보자.

이 때, 우리가 비교해야 하는 경우를 생각해 보면 A12345는 A1 * A2345, A12 * A345, ..., A1234 * A5로 나눌 수 있다.
(참고로, 행렬 곱셈은 연속되는 행렬에 대해서만 가능하기 때문에 A2* A1345와 같은 경우들은 불가능하다.)

해당 경우가 더 작은 SubProblem으로 나누어지는지 생각해 보자.
이것은 A2345, A345, ...에 대한 최소값을 구하는 SubProblem으로 생각해 볼 수 있다.

즉, 잘 생각해보면 마치 위의 피보나치수열의 예시와 비슷하게 작동하고, 해당 문제의 결과를 구하기 위해서는 좀 더 작은 문제의 정보가 필요하게 된다.

2. DP Table 정의

N개의 행렬을 곱하는 경우는 A[1:i] * A[i+1:N]으로 나눌 수 있다.

위의 식은 다음과 같은 표현이다.

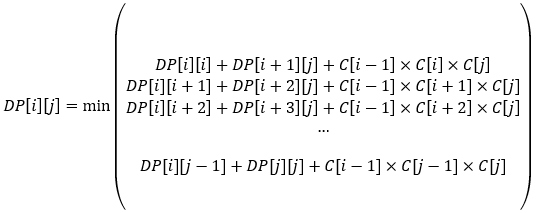
(참고)
: 크기가 A[x][y], A[y][z]인 두 행렬을 곱할 때 필요한 곱셈 연산의 횟수는
x * y * z 이다.

: i번째 행렬의 열의 크기를 C[i]라고 한다면,

A[i~k]의 크기는 C[i-1]*C[k]

A[k+1~j]의 크기는 C[K]*C[j]

따라서 두 행렬을 곱할 때 필요한 연산의 횟수는 C[i-1]*C[k]*C[j]이다.

2) 코드

DP Table의 의미

위의 그림을 참고해서 DP Table의 정의를 잘 생각해 보자.
DP[i][j]를 구할 때, DP[i:k]와 DP[k+1:j]를 활용하는데 이때 변수는 k뿐이다.

즉, DP[i:k]는 Table의 행부분을 DP[k+1:j]는 Table의 열 부분을 나타낸다고 생각할 수 있다.

DP Table을 채우는 방향

dp[i][j]를 구하기 위해서는 위에서 연결된 것들을 모두 계산해서 비교해야 한다.
즉, 왼쪽 위에서 오른족 아래의 대각선 방향으로 DP Table을 채워야 한다.

int dp[100][100];
int Matrix_chain_multiplication(int num, int C[]) {
	for(int i=1; i<=num; i++)	// dp Table 초기화
    	dp[i][i] = 0;

	// dp Table 채우기
	for(int i=1; i<=num-1; i++) {	// 대각선 number
		for(int j=0; j<num-i; j++) {	// 채울 dp Table number
        	dp[j][i+j] = INF;
            for(int k=j; k<=i+j; k++) {
            	dp[j][i+j] = min(dp[j][k]+dp[k+1][i+j]+C[j-1]*C[k]*C[i-j],
                				 dp[j][i+j]);
            }
            // path[j][i+j] = 위에서 최소가 되는 k값 
        }
	}
    return dp[0][num-1];
}

void PrintPath(int i, int j){
	if(i==j)
    	cout << "A" << i;
    else {
    	cout << "(";
        PrintPath(i, path[i][j]);
        printpath(path[i][j]+1, j);
        cout << ")";
    }
    return;
}

Time Complexity: O(n^3)

3. 최적 이진 탐색 트리

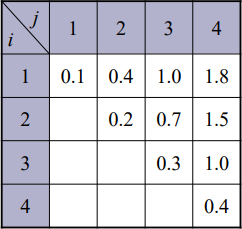
이진탐색 트리 중 각 키에 대한 검색확률이 주어졌을 때, 이를 기반으로 평균 탐색 시간이 가장 적게 걸리는 이진 탐색 트리의 모양을 찾는 문제이다.

예를들어 A, B, C 3개의 Node를 가지는 이진 트리를 구현한다고 할 때,
P(A)=0.1, P(B)=0.3, P(C)=0.6 이면

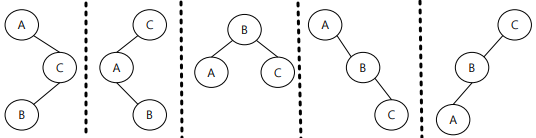
와 같이 5개의 모양을 만들 수 있고 여기서 마지막 모양이 평균 탐색 시간이 가장 적게 걸린다.

1) 아이디어

우선 가장 간단한 방법인 모든 모양을 고려해 보는 방법을 생각해 보자. 이 경우 O(2^n)의 Exponential Time이 걸린다. 즉, Time Complexity를 줄일 수 있는 새로운 방법을 생각해보아야 한다.

1. 부분 문제의 가능성 판단

5개의 Node N1, N2, N3, N4, N5으로 이진 트리를 구현하는 경우를 생각해 보자.
편의상 주어진 노드의 키 값이 N1<=N2<=N3<=N4<=N5라고 가정하자.

이때, 우리가 비교해야 하는 경우를 생각해 보면 N1이 Root인 경우, N2이 Root인 경우, ..., N5이 Root인 경우로 나눌 수 있다.

또 이 경우가 더 작은 SubProblem으로 나누어지는지 생각해보자.
이를 생각할 때 가장 중요한 것은 해당 Tree가 BST라는 것이다.

이 문제의 경우, 다음을 생각한다면 해당 문제의 결과는 이 SubTree에 대해 최솟값을 구하는 문제로 구성된다는 것을 생각할 수 있다.

왼쪽과 오른쪽에 SubTree가 존재한다.

Ni가 Root인 경우 i보다 작은노드는 왼쪽 큰 노드는 오른쪽에 들어간다.

2. DP Table 정의

n개의 노드가 주어진다고 하면 i번째 Node가 Root인 경우 A[1:i-1], A[i], A[i+1:n]으로 나눌 수 있다.

위의 식은 다음과 같은 표현이다.

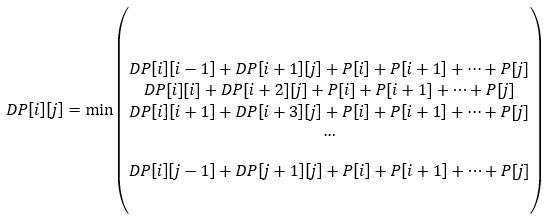
(참고)
: 어떤 노드를 탐색할 때 드는 비용(탐색시간)은 Cost = Probability * Depth이다.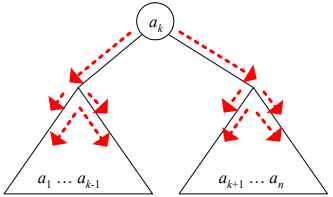

: 위의 그림을 잘 보고 생각해보면 SubTree의 정보를 활용하여 ak가 Root인 Tree를 만든다고 할 때, 각 SubTree가 만들어 질 때, ak를 거쳐서 만들어 진다.

즉, Cost = Probability * Depth이므로, 이 Depth가 Depth+1로 변경된다는 것이므로 SubTree를 구성하는 각각의 Node가 갖는 Probability를 한번 더 더해주어야 한다.

2) 코드

DP Table의 의미

위의 그림을 참고해서 DP Table의 정의를 잘 생각해 보자.
DP[i][j]를 구할 때, DP[i][k-1]와 DP[k+1][j]를 활용하는데, 이때 변수는 k뿐이다.

즉, DP[i][k-1]는 Table의 행 부분을 DP[k+1][j]는 열 부분을 나타낸다고 생각할 수 있다.

DP Table을 채우는 방향

dp[i][j]를 구하기 위해서는 위에서 연결된 것들을 모두 계산해서 비교해야 한다.
즉, 왼쪽 위에서 오른쪽 아리로의 대각선 방향으로 DP Table을 채워나가야 모든 값들을 막힘없이 구할 수 있다.

(참고로 "연쇄행렬곱셈"과는 다르게 0번 인덱스도 활용한다.)
double dp[100][100]
int Optimal_BST(int num, int P[]) {
	for(int i=1; i<=num; i++) {
    	dp[i][i] = P[i];
        result[i][i] = i;
    }

    // dp Table 채우기
    for(int i=1; i<=num-1; i++) {
    	for(int j=1; j<=num-i; j++) {
        	dp[j][i+j] = INF;
            int SUM = 0;
            for(int k=j; k<=i+j; k++)
            	SUM += P[k];
			for(int k=j; k<=i; k++) {
            	dp[j][i+j] = min(dp[j][k-1]+dp[k+1][i+j]+SUM, 
                				 dp[j][i+j]);
            }
            // result[j][i+j] = 위에서 최소가 되는 k값
        }
    }
    return dp[1][num];
}
Time Complexity: O(n^3)

4. 배낭문제(KnapSack)

무게와 가치를 갖는 N개의 Item이 주어졌을 때, 정해진 용량만 담을 수 있는 배낭에 최대한의 가치를 갖도록 Item을 넣는 문제이다.

예를들어 배낭의 정해진 용량이 30kg일 때, {가치, 무게}가 {50, 5kg}, {60, 10kg}, {140, 20kg}인 물건 3개가 있다고 해보자.

이 경우 무게당 가치가 가장 높은 물건부터 우선적으로 채우는 것은 최적의 방법이 아니다. 이 방법으로는 위의 경우 1번, 3번 물건을 채워야 하는데, 최적의 해는 2번과 3번을 채워야 하기 때문이다.

1) 아이디어

우선 가장 간단한 방법인 모든 경우의 수를 고려해 보는 방법을 생각해 보자. 이 경우 O(2^n)의 Exponential Time이 걸린다. 즉, Time Complexity를 줄일 수 있는 새로운 방법을 생각해보아야 한다.

1. 부분 문제의 가능성 판단

5개의 물건 A1, A2, A3, A4, A5로 KnapSack Problem을 해결하는 경우를 생각해 보자.
이 때, 각각의 물건의 무게와 가치를 Wi, Pi로 표현할 것이다.

이제 우리가 비교해야 할 경우를 생각해보자.
흔히 생각할 수 있는 아이디어는 A1, A2, A3, A4를 고려해 배낭에 몇개의 물건을 넣었을 때, 용량이 "M"이었을 경우 A5를 넣는다고 설정하는 것이다.

하지만 이 문제의 경우는 조금 다르게 접근해야 하는데, 비교 기준을 용량으로 해야한다.

즉, 용량이 "M"일 때, A1, A2, A3, A4, A5를 고려한 결과는

용량이 "M"이면서 A5를 반드시 넣지 않고, A1, A2, A3, A4만 고려한 결과

용량이 "M-W5"이면서 A5를 반드시 넣고, A1, A2, A3, A4를 고려한 결과

로 나눈 것과 같다는 것이다.

이렇게 나눌 경우, 해당 경우는

용량이 "M"이면서 A4를 넣지 않고 A1, A2, A3만 고려한 결과
용량이 "M-W4"이면서 A4를 넣고, A1, A2, A3를 고려한 결과

용량이 "M-W5"이면서 A4를 넣지 않고, A1, A2, A3만 고려한 결과
용량이 "M-W5-W4"이면서 A4를 넣고, A1, A2, A3를 고려한 결과

와 같이 SubProblem으로 잘 나누어 지는 것을 확인할 수 있다.

2. DP Table 정의

(참고)
최대 용량이 "M"이고 넣기를 고려하는 물건 Ai의 크기 Wi가 "M"보다 크다고 할 때에는 Ai를 넣지 않는 경우만 성립한다.

2) 코드

DP Table을 채우는 방향

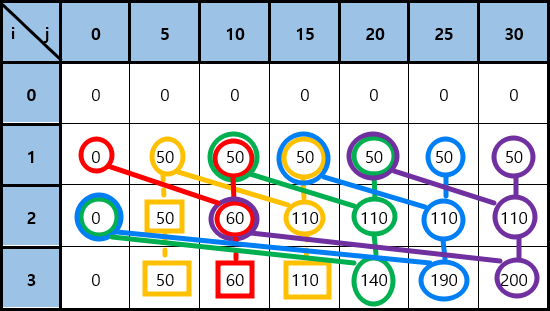
dp[i][j]를 구하기 위해서는 위에서 연결된 것들을 모두 계산해서 비교해야 한다.
즉, 위에서 아래로만 DP Table을 채워나간다면 모든 값들을 막힘없이 구할 수 있다.
int DP[10][100];

int KnapSack(int Max_Weight, int num, int W[], int P[]){
	for(int i=1; i<=num; i++) {
    	for(int j=1; j<=Max_Weight; j++){
        	if(W[i] > j)
            	DP[i][j] = DP[i-1][j];
            else
            	DP[i][j] = DP[i-1][j-W[i]]+P[i];
        }
    }
    return DP[num][Max_Weight];
}
Time Complexity: O(min(2^n, nW))

5. 가장 긴 증가하는 부분수열(LIS)

문제

수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.

예를 들어, 수열 A = {10, 20, 70, 50, 30, 40, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 70, 50, 30, 40, 50} 이고, 길이는 4이다.

해법

먼저 이 문제를 작은 문제로 나누어 보자. 이 문제는 어떤 방식으로 부분 문제를 만드는지가 중요한데, 당장 생각할 수 있는 방법은 다음이 있다.

1) DP[i]는 수열 A에서 i번째 까지의 원소 중, LIS의 크기

내가 처음 이 문제를 해결하기 위해 생각했던 방법이다.
하지만 이런 방식으로 생각을 해버리면 DP[i-1]과 DP[i]의 관계를 정하기 좀 복잡해 진다.

왜냐하면 A[i-1] < A[i]라고 해서 바로 DP를 정해버릴 수 없기 때문이다.
(A[i-1] < A[i]여도 A[i]를 선택하는 것 보다 A[i+3]를 선택하는 것이 결과적으로 LIS를 형성하게 될 수 있다.)

즉, 이런 방식으로 나눈다는 것은 최적의 부분 문제로 나누는 것이 아니게 된다.

따라서 이번엔 좀 다르게 생각해 보자.

2) DP[i]는 수열 A에서 i번째 원소를 마지막으로 가지는 LIS의 크기

이 경우에는 A[i]와 A[i-k] ( 0 <= k <= i )를 모두 비교하면, DP[i]를 만들 수 있다.

예를들어, 문제의 예시에서 DP[0] = 1, DP[1] = 2, DP[2] = 3, DP[3] = 3, DP[4] = 3까지 구한 상태라고 가정할 때 DP[5]를 구하는 과정을 생각해 보자.

A[0] < A[5], A[1] < A[5], A[2] > A[5], A[3] > A[5], A[4] < A[5] 이다.

즉, DP[0], DP[1], DP[4]만 고려하면 되고, 이중 가장 큰 값이 DP[4] 이므로 DP[5]= DP[4]+1이다.

따라서 코드는 다음과 같이 짤 수 있다.

int DP[8];
void LIS(vector<int> v) {
    fill(arr, arr + n, 1);
	for (int i = 1; i < v.size(); i++)
		for (int j = 0; j < i; j++)
			if (v[j] < v[i])
				arr[i] = max(arr[i], arr[j] + 1);
	int max = 0;
	for (int i = 0; i < v.size(); i++) {
		if (max < DP[i])
			max = DP[i];
	}
	cout << max;
}

해법

마찬가지로 이 문제를 작은 문제로 나누어 보자.

1) DP[i]는 수열 A에서 i번째 까지의 원소 중, LIS의 크기

즉, 이런 방식으로 나눈다는 것은 최적의 부분 문제로 나누는 것이 아니게 된다.

따라서 이번엔 좀 다르게 생각해 보자.

2) DP[i]는 수열 A에서 i번째 원소를 마지막으로 가지는 LIS의 크기

즉, DP[0], DP[1], DP[4]만 고려하면 되고, 이중 가장 큰 값이 DP[4] 이므로 DP[5]= DP[4]+1이다.

따라서 코드는 다음과 같이 짤 수 있다.

int DP[8];
void LIS(vector<int> v) {
    fill(arr, arr + n, 1);
	for (int i = 1; i < v.size(); i++)
		for (int j = 0; j < i; j++)
			if (v[j] < v[i])
				arr[i] = max(arr[i], arr[j] + 1);
	int max = 0;
	for (int i = 0; i < v.size(); i++) {
		if (max < DP[i])
			max = DP[i];
	}
	cout << max;
}

백준 문제

백준 1912(연속합)
백준 9465(스티커)
백준 12865(평범한 배낭)
백준 11054(바이토닉 수열)
백준 2096(내려가기)
백준 5557(1학년 상근이)
백준 1520(내리막길
백준 1915(가장 큰 정사각형)
백준 2193(이친수)
백준 14226(이모티콘)
백준 13549(숨바꼭질3)
백준 10844(쉬운 계단 수)
백준 1932(정수 삼각형)
백준 2631(줄세우기)

Ui Jin

github로 이전 중... (https://uijinee.github.io/)

이전 포스트

알고리즘 - 5. 파일압축 & 암호화

다음 포스트

알고리즘 - 6. Dynamic Programming

Algorithm

Dynamic Programming의 이해

1. 간단한 피보나치 수열

1) 코드

2) 전개 과정(그림)

3) 설명

2. DP 피보나치 수열

1) 코드

2) 전개과정(그림)

3) 설명

3. DP의 의의

DP 적용과정

DP 연습

1. String 편집 거리

1) 아이디어

1. 부분 문제의 가능성 판단

2. DP Table 정의

2) 코드

2. 연쇄 행렬 곱셈

1) 아이디어

1. 부분 문제의 가능성 판단

2. DP Table 정의

2) 코드

3. 최적 이진 탐색 트리

1) 아이디어

1. 부분 문제의 가능성 판단

2. DP Table 정의

2) 코드

DP Table의 의미

DP Table을 채우는 방향

4. 배낭문제(KnapSack)

1) 아이디어

1. 부분 문제의 가능성 판단

2. DP Table 정의

2) 코드

DP Table을 채우는 방향

5. 가장 긴 증가하는 부분수열(LIS)

문제

해법

해법

백준 문제

알고리즘 - 5. 파일압축 & 암호화

알고리즘 - 7. 그래프

0개의 댓글