논문 번역

• 이 글은 제가 읽는 논문을 번역해서 올려놓는 공간입니다.
• 번역은 LLM(현재는 GPT-4)를 통해 번역하고 있습니다.
• 대략의 pipeline은 mathpix를 통해 ocr후 gpt-4로 대략 1000토큰 단위로 나누어 번역하고 있습니다. 논문->ocr을 통한 markdown으로 변경 -> markdown로 작성된 논문을 gpt-4 api로 번역 및 markdown으로 작성
• 현재까지 완성된 파이프라인은 https://github.com/aeolian83/paper_translator 입니다
• 원문 링크는 다음과 같습니다.
  • https://arxiv.org/abs/2207.12598

분류기-프리 확산 가이던스(Classifier-Free Diffusion Guidance)

Jonathan Ho & Tim Salimans
Google 연구(Google Research), 브레인 팀(Brain team)
{jonathanho,salimans}@google.com

초록(Abstract)

분류기 가이던스(classifier guidance)는 최근에 조건부 확산 모델(conditional diffusion models)의 후속 훈련에서 모드 커버리지(mode coverage)와 샘플 충실도(sample fidelity) 사이의 균형을 맞추는 방법으로 소개되었습니다. 이는 다른 유형의 생성 모델에서 낮은 온도 샘플링(low temperature sampling)이나 절단(truncation)과 같은 정신으로 이루어집니다. 분류기 가이던스는 확산 모델의 점수 추정치(score estimate)와 이미지 분류기의 그래디언트(gradient)를 결합하여, 확산 모델과 별개로 이미지 분류기를 훈련해야 한다는 요구사항이 있습니다. 또한, 분류기 없이 가이던스를 수행할 수 있는지에 대한 질문을 제기합니다. 우리는 분류기 없이 순수 생성 모델로 가이던스를 수행할 수 있음을 보여줍니다: 우리가 분류기-프리 가이던스(classifier-free guidance)라고 부르는 것에서, 우리는 조건부와 비조건부 확산 모델을 함께 훈련하고, 결과적으로 얻은 조건부와 비조건부 점수 추정치를 결합하여, 분류기 가이던스를 사용하여 얻은 것과 유사한 샘플 품질과 다양성 사이의 균형을 달성합니다【

1 서론(INTRODUCTION)

확산 모델(diffusion models)은 최근에 표현력이 뛰어나고 유연한 생성 모델의 가족으로 부상하며, 이미지와 오디오 합성 작업에서 경쟁력 있는 샘플 품질과 가능성 점수를 제공하고 있습니다(Sohl-Dickstein et al. 2015; Song & Ermon, 2019; Ho et al. 2020; Song et al. 2021b; Kingma et al., 2021 . Song et al., 2021a). 이 모델들은 훨씬 적은 추론 단계로 자기회귀 모델(autoregressive models)의 품질에 필적하는 오디오 합성 성능을 제공했으며, FID 점수와 분류 정확도 점수 측면에서 BigGAN-deep (Brock et al. 2019)과 VQ-VAE-2 (Razavi et al. 2019)를 능가하는 ImageNet 생성 결과를 제공했습니다(Ho et al., 2021, Dhariwal & Nichol, 2021).

Dhariwal & Nichol (2021)은 추가로 훈련된 분류기를 사용하여 확산 모델의 샘플 품질을 향상시키는 기술인 분류기 가이던스를 제안했습니다. 분류기 가이던스 이전에는, 확산 모델에서 절단된 BigGAN (Brock et al. 2019)이나 낮은 온도의 Glow (Kingma & Dhariwal, 2018)와 유사한 "낮은 온도" 샘플을 생성하는 방법이 알려지지 않았습니다: 모델 점수 벡터를 스케일링하거나 확산 샘플링 중에 추가되는 가우시안 노이즈의 양을 줄이는 것과 같은 순진한 시도는 효과가 없었습니다(Dhariwal & Nichol, 2021). 대신 분류기 가이던스는 확산 모델의 점수 추정치와 로그 확률의 입력 그래디언트를 혼합합니다.

그림 1: 64x64 ImageNet 확산 모델에 대한 말라뮤트(malamute) 클래스의 분류기 없는 가이드(classifier-free guidance). 왼쪽부터 오른쪽으로: 왼쪽의 비가이드(non-guided) 샘플에서 시작하여 분류기 없는 가이드의 양을 증가시킴.

이 논문의 짧은 버전은 NeurIPS 2021 Workshop on Deep Generative Models and Downstream Applications에서 발표되었습니다: https://openreview.net/pdf?id=qw8AKxfYbI

그림 2: 각 혼합 성분이 클래스에 조건을 부여한 데이터를 나타내는 세 개의 가우스 혼합물에 대한 가이드의 영향. 가장 왼쪽의 그래프는 비가이드된 주변 밀도(non-guided marginal density)입니다. 왼쪽부터 오른쪽으로는 가이드 강도가 증가함에 따라 정규화된 가이드 조건부 혼합물의 밀도입니다.

분류기(classifier). Dhariwal & Nichol은 BigGAN의 절단 매개변수(truncation parameter)를 변화시키는 것과 유사한 방식으로 분류기 그래디언트(classifier gradient)의 강도를 변화시킴으로써 Inception 점수(Salimans et al. 2016)와 FID 점수(Heusel et al. 2017) (또는 정밀도(precision)와 재현율(recall)) 사이의 균형을 맞출 수 있습니다.

우리는 분류기 없이도 분류기 가이드(classifier guidance)를 수행할 수 있는지에 대해 관심이 있습니다. 분류기 가이드는 추가적인 분류기를 훈련해야 하고, 이 분류기는 잡음이 있는 데이터(noisy data)에 대해 훈련되어야 하기 때문에 사전 훈련된 분류기(pre-trained classifier)를 사용하는 것이 일반적으로 불가능하여 확산 모델 훈련 파이프라인(diffusion model training pipeline)을 복잡하게 만듭니다. 또한, 분류기 가이드는 샘플링 중에 점수 추정(score estimate)과 분류기 그래디언트를 혼합하기 때문에, 분류기 가이드된 확산 샘플링(classifier-guided diffusion sampling)은 그래디언트 기반의 적대적 공격(gradient-based adversarial attack)으로 이미지 분류기(image classifier)를 혼란시키려는 시도로 해석될 수 있습니다. 이는 분류기 가이드가 FID와 Inception 점수(IS)와 같은 분류기 기반 메트릭(classifier-based metrics)을 향상시키는 데 성공적인 것이 단순히 해당 분류기에 대한 적대적 행위(adversarial against such classifiers) 때문인지에 대한 의문을 제기합니다. 분류기 그래디언트 방향으로 나아가는 것은 GAN 훈련, 특히 비매개변수 생성기(nonparameteric generators)와도 어느 정도 유사성이 있으며, 이는 또한 분류기 가이드된 확산 모델이 이미 해당 메트릭에서 잘 수행되는 것으로 알려진 GAN과 유사해지기 시작하기 때문에 분류기 기반 메트릭에서 잘 수행하는지에 대한 의문을 제기합니다.

이러한 질문들을 해결하기 위해, 우리는 분류기(classifier)를 전혀 사용하지 않는 우리의 안내 방법인 분류기-자유 안내(classifier-free guidance)를 제시합니다. 이미지 분류기의 그래디언트 방향으로 샘플링하는 대신, 분류기-자유 안내는 조건부 확산 모델(conditional diffusion model)의 점수 추정치와 함께 훈련된 비조건부 확산 모델(unconditional diffusion model)의 점수 추정치를 혼합합니다. 혼합 가중치를 조절함으로써, 우리는 분류기 안내(classifier guidance)에 의해 달성된 것과 유사한 FID/IS 트레이드오프(tradeoff)를 얻을 수 있습니다. 우리의 분류기-자유 안내 결과는 순수 생성적 확산 모델(pure generative diffusion models)이 다른 유형의 생성 모델로 가능한 매우 높은 충실도(high fidelity) 샘플을 합성할 수 있음을 보여줍니다.

2 BACKGROUND

우리는 연속 시간(continuous time)에서 확산 모델(diffusion models)을 훈련합니다(Song et al., 2021b; Chen et al., 2021, Kingma et al. 2021): $\mathbf{x} \sim p(\mathbf{x})$와 $\mathbf{z}=\left\{\mathbf{z}_{\lambda} \mid \lambda \in\left[\lambda_{\min }, \lambda_{\max }\right]\right\}$에 대해 하이퍼파라미터(hyperparameters) $\lambda_{\min }<\lambda_{\max } \in \mathbb{R}$를 사용하여, 전방 과정(forward process) $q(\mathbf{z} \mid \mathbf{x})$는 분산을 보존하는 마르코프 과정(variance-preserving Markov process) (Sohl-Dickstein et al. 2015)입니다:

우리는 $p(\mathbf{z})$ (또는 $p\left(\mathbf{z}_{\lambda}\right)$)를 $\mathbf{x} \sim p(\mathbf{x})$ 및 $\mathbf{z} \sim q(\mathbf{z} \mid \mathbf{x})$일 때 $\mathbf{z}$ (또는 $\mathbf{z}_{\lambda}$)의 주변 확률(marginal)을 나타내는 표기법으로 사용할 것입니다. $\lambda=\log \alpha_{\lambda}^{2} / \sigma_{\lambda}^{2}$이므로, $\lambda$는 $\mathbf{z}_{\lambda}$의 로그 신호 대 잡음비(log signal-to-noise ratio)로 해석될 수 있으며, 전방 과정(forward process)은 $\lambda$가 감소하는 방향으로 진행됩니다.

$\mathbf{x}$에 조건을 달고, 전방 과정은 역방향으로 $q\left(\mathbf{z}_{\lambda^{\prime}} \mid \mathbf{z}_{\lambda}, \mathbf{x}\right)=$ $\mathcal{N}\left(\tilde{\boldsymbol{\mu}}_{\lambda^{\prime} \mid \lambda}\left(\mathbf{z}_{\lambda}, \mathbf{x}\right), \tilde{\sigma}_{\lambda^{\prime} \mid \lambda}^{2} \mathbf{I}\right)$의 전이로 설명될 수 있습니다. 여기서

역방향 과정(reverse process) 생성 모델은 $p_{\theta}\left(\mathbf{z}_{\lambda_{\min }}\right)=\mathcal{N}(\mathbf{0}, \mathbf{I})$에서 시작합니다. 우리는 전이를 명시합니다:

샘플링하는 동안, 우리는 증가하는 순서 $\lambda_{\min}=\lambda_{1}<\cdots<\lambda_{T}=\lambda_{\max}$를 따라 $T$ 타임스텝 동안 이 전이를 적용합니다; 즉, 우리는 Sohl-Dickstein et al. (2015); Ho et al. (2020)의 이산 시간 조상 샘플러(discrete time ancestral sampler)를 따릅니다. 모델 $\mathbf{x}_{\theta}$가 정확하다면, $T \rightarrow \infty$일 때, 우리는 $p(\mathbf{z})$로 분포하는 SDE의 샘플 경로를 얻게 되며, 연속 시간 모델 분포를 나타내기 위해 $p_{\theta}(\mathbf{z})$를 사용합니다(Song et al. 2021b). 분산은 Nichol & Dhariwal (2021)이 제안한 대로 $\tilde{\sigma}_{\lambda^{\prime} \mid \lambda}^{2}$와 $\sigma_{\lambda \mid \lambda^{\prime}}^{2}$의 로그 공간 보간입니다; 우리는 학습된 $\mathbf{z}_{\lambda}$-의존적인 $v$보다는 상수 하이퍼파라미터 $v$를 사용하는 것이 효과적이라는 것을 발견했습니다. $\lambda^{\prime} \rightarrow \lambda$로 갈수록 분산은 $\tilde{\sigma}_{\lambda^{\prime} \mid \lambda}^{2}$로 단순화되므로, $v$는 실제로 비무한소 타임스텝으로 샘플링할 때만 영향을 미칩니다.

역과정 평균(reverse process mean)은 추정치 $\mathbf{x}_{\theta}\left(\mathbf{z}_{\lambda}\right) \approx \mathbf{x}$를 $q\left(\mathbf{z}_{\lambda^{\prime}} \mid \mathbf{z}_{\lambda}, \mathbf{x}\right)$에 대입한 것에서 나옵니다(Ho et al. 2020, Kingma et al. 2021) ($x_{\theta}$는 또한 $\lambda$를 입력으로 받지만, 표기를 간결하게 하기 위해 이를 생략합니다). 우리는 $\mathbf{x}_{\theta}$를 $\boldsymbol{\epsilon}$-예측에 관한 것으로 파라미터화합니다(Ho et al. 2020): $\mathbf{x}_{\theta}\left(\mathbf{z}_{\lambda}\right)=\left(\mathbf{z}_{\lambda}-\sigma_{\lambda} \boldsymbol{\epsilon}_{\theta}\left(\mathbf{z}_{\lambda}\right)\right) / \alpha_{\lambda}$, 그리고 우리는 다음 목표로 학습합니다.

여기서 $\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}), \mathbf{z}_{\lambda}=\alpha_{\lambda} \mathbf{x}+\sigma_{\lambda} \boldsymbol{\epsilon}$이고, $\lambda$는 $\left[\lambda_{\min }, \lambda_{\max }\right]$ 범위에서 분포 $p(\lambda)$를 따라 추출됩니다. 이 목표는 다중 노이즈 스케일에서의 노이즈 제거 점수 매칭(denoising score matching)입니다(Vincent. 2011, Hyvärinen & Dayan 2005), 그리고 $p(\lambda)$가 균등 분포일 때, 이 목표는 잠재 변수 모델(latent variable model)의 주변 로그 가능도(marginal log likelihood)에 대한 변분 하한(variational lower bound)에 비례합니다. $\int p_{\theta}(\mathbf{x} \mid \mathbf{z}) p_{\theta}(\mathbf{z}) d \mathbf{z}$, 여기서 명시되지 않은 디코더 $p_{\theta}(\mathbf{x} \mid \mathbf{z})$와 $\mathbf{z}_{\lambda_{\min }}$에서의 사전 분포(prior)에 대한 항은 무시합니다(Kingma et al. 2021).

$p(\lambda)$가 균일하지 않은 경우, 이 목적은 샘플 품질(Ho et al., 2020, Kingma et al. 2021)을 조정할 수 있는 가중 변분 하한(weighted variational lower bound)으로 해석될 수 있습니다. 우리는 Nichol & Dhariwal (2021)의 이산 시간 코사인 노이즈 스케줄(discrete time cosine noise schedule)에서 영감을 받은 $p(\lambda)$를 사용합니다: 우리는 $\lambda$를 $\lambda=-2 \log \tan (a u+b)$를 통해 샘플링합니다. 여기서 $u \in[0,1]$는 균일하게 분포되어 있고, $b=\arctan \left(e^{-\lambda_{\max } / 2}\right)$, $a=\arctan \left(e^{-\lambda_{\min } / 2}\right)-b$입니다. 이것은 유계 구간(bounded interval)에서 지지되도록 수정된 쌍곡 세컨트 분포(hyperbolic secant distribution)를 나타냅니다. 유한 타임스텝 생성(finite timestep generation)을 위해, 우리는 균일하게 분포된 $u \in[0,1]$에 해당하는 $\lambda$ 값을 사용하고, 최종 생성된 샘플은 $\mathbf{x}_{\theta}\left(\mathbf{z}_{\lambda_{\max }}\right)$입니다.

$\epsilon_{\theta}\left(\mathbf{z}_{\lambda}\right)$에 대한 손실은 모든 $\lambda$에 대해 노이즈 점수 매칭(denoising score matching)이기 때문에, 우리 모델에 의해 학습된 점수 $\epsilon_{\theta}\left(\mathbf{z}_{\lambda}\right)$는 우리의 노이즈 데이터 $\mathbf{z}_{\lambda}$의 분포 로그 밀도(log-density)의 그래디언트를 추정합니다. 즉, $\boldsymbol{\epsilon}_{\theta}\left(\mathbf{z}_{\lambda}\right) \approx-\sigma_{\lambda} \nabla_{\mathbf{z}_{\lambda}} \log p\left(\mathbf{z}_{\lambda}\right)$입니다; 그러나, 우리가 $\epsilon_{\theta}$를 정의하기 위해 제약이 없는 신경망(unconstrained neural networks)을 사용하기 때문에, $\epsilon_{\theta}$의 그래디언트가 되는 어떤 스칼라 포텐셜(scalar potential)이 존재할 필요는 없습니다. 학습된 확산 모델(diffusion model)에서 샘플링하는 것은 원래 데이터 $\mathbf{x}$의 조건부 분포(conditional distribution) $p(\mathbf{x})$로 수렴하는 일련의 분포 $p\left(\mathbf{z}_{\lambda}\right)$에서 랑제뱅 확산(Langevin diffusion)을 사용하여 샘플링하는 것과 유사합니다.

조건부 생성 모델링(conditional generative modeling)의 경우, 데이터 $\mathbf{x}$는 조건 정보 $\mathbf{c}$와 함께 추출됩니다. 예를 들어, 클래스 조건부 이미지 생성(class-conditional image generation)을 위한 클래스 레이블입니다. 모델에 대한 유일한 수정은 역과정 함수 근사자(reverse process function approximator)가 $\mathbf{c}$를 입력으로 받는다는 것입니다. 예를 들어 $\epsilon_{\theta}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)$와 같이 말이죠.

3 지도(GuIdANCE)

GANs(Generative Adversarial Networks)나 플로우 기반 모델(flow-based models)과 같은 특정 생성 모델의 흥미로운 특성 중 하나는 샘플링 시 생성 모델에 입력되는 노이즈의 분산이나 범위를 줄여서 절단(truncated) 샘플링이나 저온도(low temperature) 샘플링을 수행할 수 있다는 것입니다. 의도된 효과는 샘플의 다양성을 감소시키면서 각 개별 샘플의 품질을 향상시키는 것입니다. 예를 들어, BigGAN(Brock et al. 2019)에서의 절단은 절단량이 적고 많을 때 각각 FID 점수와 Inception 점수 사이의 트레이드오프 곡선을 생성합니다. Glow(Kingma & Dhariwal. 2018)에서의 저온도 샘플링도 비슷한 효과를 가집니다.

불행히도, 확산 모델(diffusion models)에서 절단이나 저온도 샘플링을 구현하려는 직접적인 시도는 효과적이지 않습니다. 예를 들어, 모델 점수를 조정하거나 역과정에서 가우시안 노이즈의 분산을 줄이는 것은 확산 모델이 흐릿하고 저품질의 샘플을 생성하게 만듭니다(Dhariwal & Nichol, 2021).

3.1 분류기 가이던스(CLASSIFIER GUIDANCE)

확산 모델에서 절단과 유사한 효과를 얻기 위해, Dhariwal & Nichol (2021)은 분류기 가이던스(classifier guidance)를 도입합니다. 여기서 확산 점수 $\boldsymbol{\epsilon}_{\theta}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right) \approx-\sigma_{\lambda} \nabla_{\mathbf{z}_{\lambda}} \log p\left(\mathbf{z}_{\lambda} \mid \mathbf{c}\right)$는 다음과 같이 보조 분류기 모델 $p_{\theta}\left(\mathbf{c} \mid \mathbf{z}_{\lambda}\right)$의 로그 가능도(log likelihood)의 기울기를 포함하도록 수정됩니다:

여기서 $w$는 분류기(classifier) 지도의 강도를 조절하는 매개변수입니다. 수정된 점수 $\tilde{\boldsymbol{\epsilon}}_{\theta}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)$는 $\boldsymbol{\epsilon}_{\theta}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)$ 대신에 확산 모델(diffusion model)에서 샘플링할 때 사용되며, 이로 인해 대략적인 샘플이 다음 분포에서 생성됩니다.

이 효과는 분류기 $p_{\theta}\left(\mathbf{c} \mid \mathbf{z}_{\lambda}\right)$가 올바른 레이블(label)에 높은 가능성을 할당하는 데이터의 확률을 높이는 것입니다: 잘 분류될 수 있는 데이터는 인셉션 점수(Inception score)에서 높은 점수를 받으며, 이는 인지적 품질(perceptual quality)에 대한 평가로서, 생성 모델(generative models)이 이를 설계적으로 보상받도록 합니다(Salimans et al. 2016). 따라서 Dhariwal & Nichol은 $w>0$으로 설정함으로써 그들의 확산 모델의 인셉션 점수를 향상시킬 수 있었으나, 샘플의 다양성이 감소하는 대가를 치렀습니다.

그림 2는 각 클래스에 대한 조건부 분포가 등방성 가우시안(isotropic Gaussian)인 세 클래스의 장난감 $2 \mathrm{D}$ 예시에서 수치적으로 해결된 지도 $\tilde{p}_{\theta}\left(\mathbf{z}_{\lambda} \mid \mathbf{c}\right) \propto p_{\theta}\left(\mathbf{z}_{\lambda} \mid \mathbf{c}\right) p_{\theta}\left(\mathbf{c} \mid \mathbf{z}_{\lambda}\right)^{w}$의 효과를 보여줍니다. 지도를 적용한 후 각 조건부의 형태는 뚜렷하게 비가우시안(non-Gaussian)입니다. 지도의 강도가 증가함에 따라 각 조건부는 다른 클래스로부터 멀어지고 로지스틱 회귀(logistic regression)에 의해 주어진 높은 확신의 방향으로 확률 질량을 배치하며, 대부분의 질량은 더 작은 영역에 집중됩니다. 이러한 행동은 분류기 지도의 강도가 증가할 때 ImageNet 모델에서 발생하는 인셉션 점수 증가와 샘플 다양성 감소의 단순한 현상으로 볼 수 있습니다.

가중치 $w+1$을 가진 분류기(classifier) 가이던스를 조건 없는 모델(unconditional model)에 적용하는 것은 이론적으로 가중치 $w$를 가진 분류기 가이던스를 조건 있는 모델(conditional model)에 적용하는 것과 동일한 결과를 가져옵니다. 왜냐하면 $p_{\theta}\left(\mathbf{z}_{\lambda} \mid \mathbf{c}\right) p_{\theta}\left(\mathbf{c} \mid \mathbf{z}_{\lambda}\right)^{w} \propto p_{\theta}\left(\mathbf{z}_{\lambda}\right) p_{\theta}\left(\mathbf{c} \mid \mathbf{z}_{\lambda}\right)^{w+1} ;$ 또는 점수(score) 측면에서 보면,

하지만 흥미롭게도, Dhariwal & Nichol은 조건 없는 모델(unconditional model)에 가이던스를 적용하는 것이 아니라 이미 조건 있는 모델(class-conditional model)에 분류기 가이던스를 적용할 때 최상의 결과를 얻었습니다. 이러한 이유로, 우리는 이미 조건이 있는 모델에 가이던스를 적용하는 설정을 유지할 것입니다.

3.2 분류기 없는 가이던스(CLASSIFIER-FREE GUIDANCE)

분류기 가이던스는 절단(truncation)이나 낮은 온도 샘플링(low temperature sampling)에서 기대되는 것처럼 IS와 FID 사이의 균형을 성공적으로 맞추지만, 그럼에도 불구하고 이미지 분류기(image classifier)로부터의 기울기(gradients)에 의존하고 있으며, 우리는 섹션 11에서 언급한 이유로 분류기를 제거하고자 합니다. 여기서, 우리는 분류기 없는 가이던스(classifier-free guidance)를 설명하는데, 이는 그러한 기울기 없이도 동일한 효과를 달성합니다. 분류기 없는 가이던스는 분류기 없이도 분류기 가이던스와 같은 효과를 내기 위해 $\epsilon_{\theta}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)$를 수정하는 대안적인 방법입니다. 알고리즘 1과 2는 분류기 없는 가이던스를 사용한 훈련과 샘플링을 자세히 설명합니다.

별도의 분류기 모델을 훈련하는 대신, 조건부 모델 $p_{\theta}(\mathbf{z} \mid \mathbf{c})$과 함께 조건이 없는(unconditional) 노이즈 제거 확산 모델 $p_{\theta}(\mathbf{z})$을 스코어 추정기 $\epsilon_{\theta}\left(\mathbf{z}_{\lambda}\right)$를 통해 파라미터화하여 훈련하기로 결정했습니다. 조건부 모델은 $\boldsymbol{\epsilon}_{\theta}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)$를 통해 파라미터화됩니다. 우리는 두 모델 모두를 파라미터화하기 위해 단일 신경망을 사용하는데, 조건이 없는 모델의 경우 클래스 식별자 $\mathbf{c}$에 대해 null 토큰 $\varnothing$을 입력하여 스코어를 예측할 수 있습니다. 즉, $\epsilon_{\theta}\left(\mathbf{z}_{\lambda}\right)=\epsilon_{\theta}\left(\mathbf{z}_{\lambda}, \mathbf{c}=\varnothing\right)$입니다. 우리는 조건이 없는(unconditional) 모델과

조건부 모델을 함께 훈련하는데, 단순히 클래스 식별자 $\mathbf{c}$를 일정 확률 $p_{\text {uncond }}$로 조건이 없는 클래스 식별자 $\varnothing$로 무작위로 설정함으로써 이를 수행합니다. 이 확률은 하이퍼파라미터로 설정됩니다. (분명히, 별도의 모델을 훈련하는 것도 가능하지만, 우리는 공동 훈련을 선택했습니다. 왜냐하면 이는 구현하기 매우 간단하고, 훈련 파이프라인을 복잡하게 만들지 않으며, 전체 파라미터 수를 증가시키지 않기 때문입니다.) 그런 다음 우리는 조건부와 조건이 없는 스코어 추정치의 다음과 같은 선형 조합을 사용하여 샘플링을 수행합니다:

식 (6)에는 분류기 그래디언트가 존재하지 않으므로, $\tilde{\epsilon}_{\theta}$ 방향으로 한 걸음을 내딛는 것은 이미지 분류기에 대한 그래디언트 기반 적대적 공격으로 해석될 수 없습니다. 더욱이, $\tilde{\epsilon}_{\theta}$는 제약이 없는 신경망의 사용으로 인해 비보존적(non-conservative) 벡터 필드인 스코어 추정치로 구성되므로, $\tilde{\boldsymbol{\epsilon}}_{\theta}$가 분류기 가이드 스코어인 분류기 로그 가능성과 같은 스칼라 포텐셜이 일반적으로 존재할 수 없습니다.

Eq. (6)에 해당하는 분류기가 일반적으로 존재하지 않을 수도 있지만, 실제로는 암시적 분류기 $p^{i}\left(\mathbf{c} \mid \mathbf{z}_{\lambda}\right) \propto p\left(\mathbf{z}_{\lambda} \mid \mathbf{c}\right) / p\left(\mathbf{z}_{\lambda}\right)$의 기울기에서 영감을 받았습니다. 만약 우리가 정확한 점수 $\boldsymbol{\epsilon}^{*}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)$와 $\boldsymbol{\epsilon}^{*}\left(\mathbf{z}_{\lambda}\right)$ (각각 $p\left(\mathbf{z}_{\lambda} \mid \mathbf{c}\right)$와 $p\left(\mathbf{z}_{\lambda}\right)$에 대한)에 접근할 수 있다면, 이 암시적 분류기의 기울기는 $\nabla_{\mathbf{z}_{\lambda}} \log p^{i}\left(\mathbf{c} \mid \mathbf{z}_{\lambda}\right)=-\frac{1}{\sigma_{\lambda}}\left[\boldsymbol{\epsilon}^{*}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)-\boldsymbol{\epsilon}^{*}\left(\mathbf{z}_{\lambda}\right)\right]$가 될 것이고, 이 암시적 분류기를 사용한 분류 가이드는 점수 추정치를 $\tilde{\epsilon}^{*}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)=$ $(1+w) \boldsymbol{\epsilon}^{*}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)-w \boldsymbol{\epsilon}^{*}\left(\mathbf{z}_{\lambda}\right)$로 수정할 것입니다. Eq. 6과의 유사성을 주목하지만, $\tilde{\boldsymbol{\epsilon}}^{*}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)$가 $\tilde{\boldsymbol{\epsilon}}_{\theta}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)$와 근본적으로 다르다는 것도 주목해야 합니다. 전자는 스케일된 분류기 기울기 $\boldsymbol{\epsilon}^{*}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)-\boldsymbol{\epsilon}^{*}\left(\mathbf{z}_{\lambda}\right)$에서 구성되며, 후자는 추정치 $\epsilon_{\theta}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)-\boldsymbol{\epsilon}_{\theta}\left(\mathbf{z}_{\lambda}\right)$에서 구성되고, 이 표현은 일반적으로 어떤 분류기의 (스케일된) 기울기가 아닙니다. 다시 말해, 점수 추정치는 제약이 없는 신경망(neural networks)의 출력이기 때문입니다.

생성 모델을 베이즈 규칙(Bayes' rule)을 사용하여 뒤집는 것이 유용한 지도 신호를 제공하는 좋은 분류기를 만들어낸다는 것은 사전에 명백하지 않습니다. 예를 들어, Grandvalet & Bengio (2004)는 생성 모델에서 파생된 암시적 분류기가 그 생성 모델이 데이터 분포와 정확히 일치하는 인공적인 경우에도 일반적으로 판별 모델(discriminative models)보다 성능이 떨어진다는 것을 발견했습니다. 우리의 경우처럼 모델이 잘못 지정될 것으로 예상되는 상황에서, 베이즈 규칙에 의해 파생된 분류기는 일관성이 없을 수 있습니다(Grünwald & Langford, 2007) 그리고 그들의 성능에 대한 모든 보장을 잃게 됩니다. 그럼에도 불구하고, 4장에서 우리는 분류기 없는 지도(classifier-free guidance)가 분류기 지도(classifier guidance)와 마찬가지로 FID와 IS 사이의 균형을 맞출 수 있다는 것을 경험적으로 보여줍니다. 5장에서는 분류기 없는 지도가 분류기 지도와 관련하여 시사하는 바에 대해 논의합니다.

4 실험

우리는 분류기 없는 지도를 사용하여 클래스 조건부 ImageNet(Russakovsky et al. 2015)에 대한 확산 모델(diffusion models)을 훈련시킵니다. 이는 BigGAN 논문(Brock et al. 2019)부터 시작하여 FID와 Inception 점수 사이의 균형을 연구하기 위한 표준 설정입니다.

우리 실험의 목적은 분류기 없는 지도가 분류기 지도와 유사한 FID/IS 균형을 달성할 수 있음을 증명하는 개념 증명(proof of concept)으로서, 반드시 최신 기술의 샘플 품질 지표를 끌어올리기 위한 것은 아닙니다.

그림 3: 128x128 ImageNet에서의 분류기 없는 지도. 왼쪽: 비지도 샘플, 오른쪽: $w=3.0$인 분류기 없는 지도 샘플. 흥미롭게도, 이렇게 강하게 지도된 샘플은 채도가 높은 색상을 나타냅니다. 더 많은 예시는 그림 8을 참조하세요.

이 벤치마크에서. 이를 위해, 우리는 Dhariwal & Nichol (2021)의 지도된 확산 모델과 동일한 모델 구조와 하이퍼파라미터를 사용합니다(2장에서 명시된 연속 시간 훈련을 제외하고); 이 하이퍼파라미터 설정은 분류기 지도를 위해 조정되었으므로 분류기 없는 지도에는 최적이 아닐 수 있습니다. 또한, 우리는 조건부와 비조건부 모델을 별도의 분류기 없이 동일한 구조로 통합하기 때문에, 실제로는 이전 연구보다 적은 모델 용량을 사용하고 있습니다. 그럼에도 불구하고, 우리의 분류기 없는 지도 모델은 여전히 경쟁력 있는 샘플 품질 지표를 생산하며 때때로 이전 연구를 능가하기도 합니다. 다음 절에서 이를 볼 수 있습니다.

4.1 분류기 없는 지도 강도 변화

이 논문의 주요 주장을 실험적으로 검증합니다: 분류기 없는 가이던스(classifier-free guidance)가 분류기 가이던스(classifier guidance)나 GAN 절단(GAN truncation)처럼 IS(Inception Score)와 FID(Fréchet Inception Distance) 사이의 균형을 맞출 수 있다는 것입니다. 우리는 제안한 분류기 없는 가이던스를 $64 \times 64$ 및 $128 \times 128$ 클래스 조건부 ImageNet 생성에 적용합니다. 표 1과 그림 4에서는 가이던스 강도 $w$를 변경하면서 $64 \times 64$ ImageNet 모델의 샘플 품질 효과를 보여줍니다; 표 2와 그림 5는 $128 \times 128$ 모델에 대해 동일한 내용을 보여줍니다. 우리는 $w \in\{0,0.1,0.2, \ldots, 4\}$를 고려하고 Heusel et al. (2017)과 Salimans et al. (2016)의 절차에 따라 각 값에 대해 50000개의 샘플로 FID와 Inception Score를 계산합니다. 모든 모델은 로그 SNR(log SNR) 끝점 $\lambda_{\min }=-20$과 $\lambda_{\max }=20$을 사용했습니다. $64 \times 64$ 모델은 샘플러 노이즈 보간 계수 $v=0.3$을 사용하고 40만 단계를 학습했으며; $128 \times 128$ 모델은 $v=0.2$를 사용하고 270만 단계를 학습했습니다.

우리는 작은 양의 가이던스 $(w=0.1$ 또는 $w=0.3$, 데이터셋에 따라 다름)로 가장 좋은 FID 결과를 얻고, 강한 가이던스 $(w \geq 4)$로 가장 좋은 IS 결과를 얻습니다. 이 두 극단 사이에서 우리는 이 두 인식 품질 지표 사이의 명확한 균형을 볼 수 있으며, FID는 $w$가 증가함에 따라 단조롭게 감소하고 IS는 단조롭게 증가합니다. 우리의 결과는 Dhariwal & Nichol (2021)과 Ho et al. (2021)에 비해 유리하며, 실제로 우리의 $128 \times 128$ 결과는 문헌에서 최고의 성과를 보여줍니다. $w=0.3$에서, 우리 모델의 FID 점수는 $128 \times 128$ ImageNet에서 분류기 가이드 ADM-G를 능가하며, $w=4.0$에서, 우리 모델은 BigGAN-deep이 최고의 IS 절단 수준에서 평가될 때 FID와 IS 모두에서 BigGAN-deep을 능가합니다.

그림 1, 3 및 6에서 8까지는 다양한 수준의 가이던스에 대해 우리 모델에서 무작위로 생성된 샘플을 보여줍니다: 여기서 우리는 분류기 없는 가이던스 강도를 증가시키면 예상대로 샘플 다양성이 감소하고 개별 샘플 충실도가 증가하는 것을 명확하게 볼 수 있습니다.

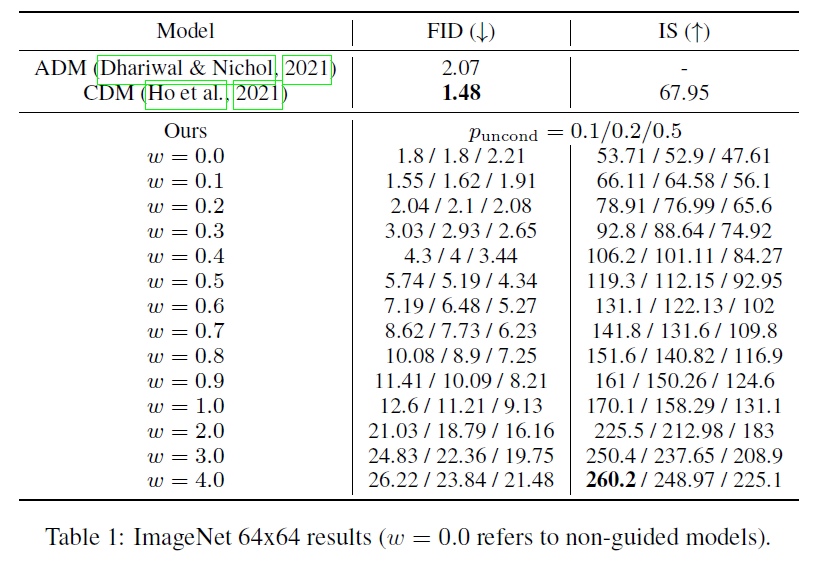
표 1: ImageNet 64x64 결과 ($w=0.0$은 비지도 모델을 의미합니다).

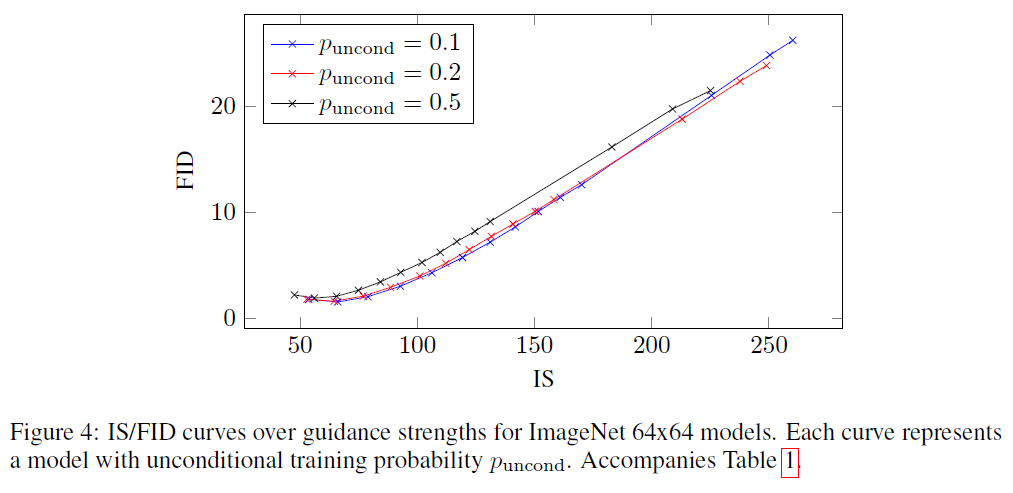
그림 4: ImageNet 64x64 모델에 대한 지도 강도에 따른 IS/FID 곡선. 각 곡선은 무조건적 학습 확률 $p_{\text{uncond}}$를 가진 모델을 나타냅니다. 표 1과 함께 제공됩니다.

4.2 무조건적 학습 확률 변화

분류기 없는 지도(classifier-free guidance)의 주요 하이퍼파라미터는 학습 시간에 조건부 및 무조건부 확산 모델의 공동 학습 중 무조건적 생성에 대한 학습 확률인 $p_{\text{uncond}}$입니다. 여기서는 $64 \times 64$ ImageNet에서 다양한 $p_{\text{uncond}}$에 대한 모델 학습의 영향을 연구합니다.

표 1과 그림 4는 $p_{\text{uncond}}$가 샘플 품질에 미치는 영향을 보여줍니다. 우리는 $p_{\text{uncond}} \in \{0.1,0.2,0.5\}$인 모델을 각각 40만 학습 단계로 학습시키고, 다양한 지도 강도에서 샘플 품질을 평가했습니다. 우리는 $p_{\text{uncond}}=0.5$가 IS/FID 프론티어 전체에서 $p_{\text{uncond}} \in \{0.1,0.2\}$보다 일관되게 성능이 떨어진다는 것을 발견했습니다; $p_{\text{uncond}} \in \{0.1,0.2\}$는 서로 비슷한 수준으로 잘 수행됩니다.

이러한 발견을 바탕으로, 샘플 품질에 효과적인 분류기 없는 지도 점수를 생성하기 위해서는 확산 모델의 모델 용량 중 상대적으로 작은 부분만이 무조건적 생성 작업에 할당되어야 한다는 결론을 내립니다. 흥미롭게도, 분류기 지도(classifier guidance)에 대해 Dhariwal & Nichol은 효과적인 분류기 지도 샘플링을 위해 상대적으로 작은 용량의 분류기가 충분하다고 보고하며, 이는 우리가 분류기 없는 지도 모델에서 발견한 현상을 반영합니다.

4.3 샘플링 단계 수 변화

확산 모델의 샘플 품질에 샘플링 단계 수 $T$가 중요한 영향을 미친다는 것이 알려져 있기 때문에, 여기서는 $128 \times 128$ ImageNet 모델에서 $T$를 변화시키는 효과를 연구합니다. 표 2와 그림 5는 다양한 지도 강도에서 $T \in \{128,256,1024\}$를 변화시키는 효과를 보여줍니다. 예상대로, $T$가 증가함에 따라 샘플 품질이 향상되며, 이 모델의 경우 $T=256$이 샘플 품질과 샘플링 속도 사이의 좋은 균형을 달성합니다.

$T=256$은 ADM-G(Dhariwal & Nichol, 2021)에서 사용된 샘플링 단계의 수와 대략 같으며, 우리의 모델이 이를 능가합니다. 그러나 우리 방법의 각 샘플링 단계는 조건부 $\epsilon_{\theta}\left(\mathbf{z}_{\lambda}, \mathbf{c}\right)$와 비조건부 $\epsilon_{\theta}\left(\mathbf{z}_{\lambda}\right)$에 대해 각각 한 번씩, 총 두 번의 잡음 제거 모델 평가를 필요로 한다는 점을 주목해야 합니다. 우리는 ADM-G와 동일한 모델 구조를 사용했기 때문에, 샘플링 속도 측면에서 공정한 비교를 위해서는 우리의 $T=128$ 설정을 봐야 하며, 이는 FID 점수 측면에서 ADM-G에 비해 성능이 떨어집니다.

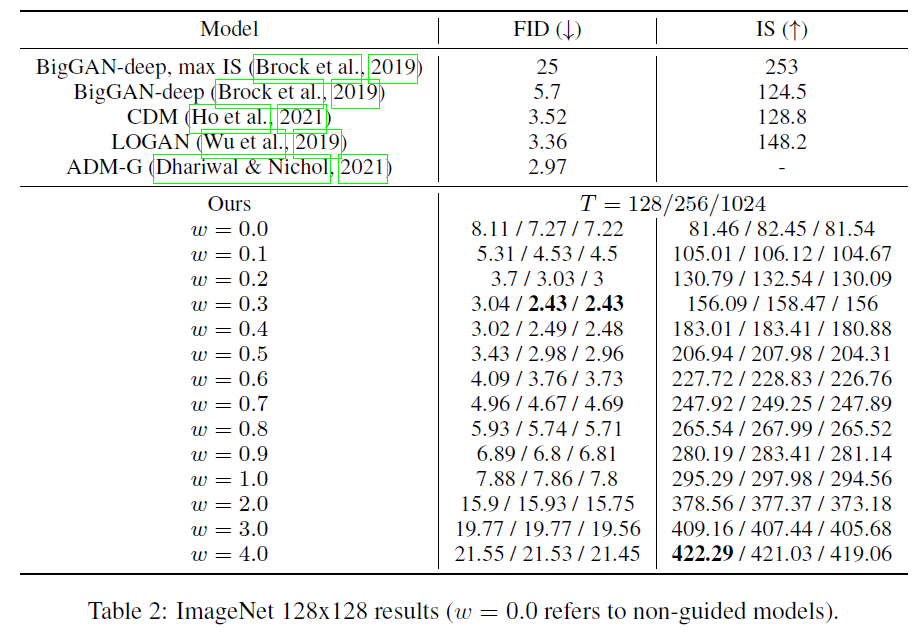
표 2: ImageNet $128 \times 128$ 결과 ($w=0.0$은 비지도 모델을 의미합니다).

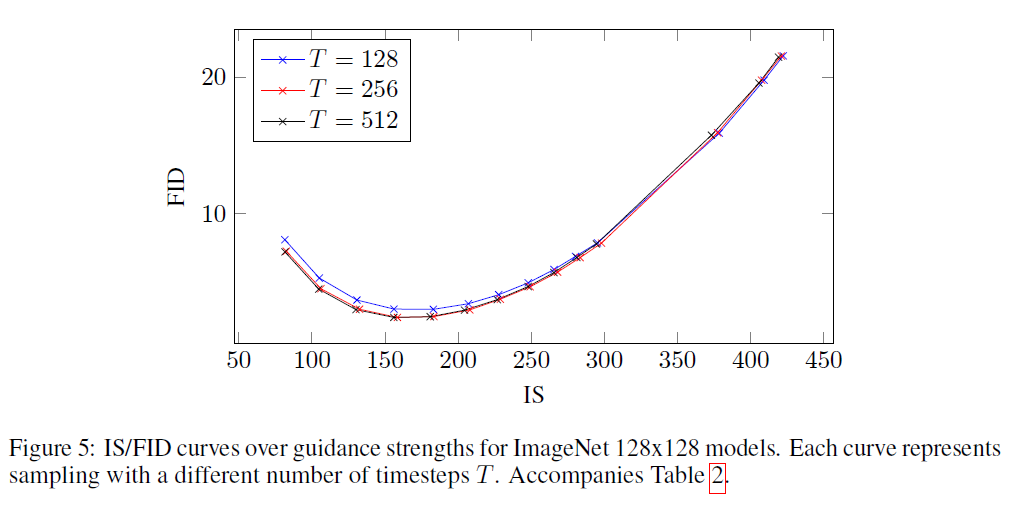
그림 5: ImageNet 128x128 모델에 대한 지도 강도에 따른 IS/FID 곡선. 각 곡선은 다른 시간 단계 $T$로 샘플링할 때를 나타냅니다. 표 2와 함께 제공됩니다.

5 토론

우리의 분류기-자유(classifier-free) 지도 방법의 가장 실용적인 장점은 극도로 단순하다는 것입니다: 훈련 중에는 조건부를 무작위로 드롭아웃하는 한 줄짜리 코드 변경이 필요하고, 샘플링 중에는 조건부와 비조건부 점수 추정치를 혼합하는 것입니다. 반면, 분류기 지도(classifier guidance)는 추가 분류기를 훈련해야 하므로 훈련 파이프라인을 복잡하게 만듭니다. 이 분류기는 잡음이 있는 $\mathbf{z}_{\lambda}$에 대해 훈련되어야 하므로, 표준 사전 훈련된 분류기를 그대로 사용할 수 없습니다.

분류기-자유 지도는 추가로 훈련된 분류기 없이도 분류기 지도처럼 IS와 FID를 조절할 수 있기 때문에, 순수 생성 모델(pure generative model)만으로도 지도가 가능하다는 것을 우리는 입증했습니다. 더욱이, 우리의 확산 모델(diffusion models)은 제약이 없는 신경망으로 매개변수화되어 있으므로, 그들의 점수 추정치는 분류기 그라디언트(classifier gradients)와 달리 반드시 보존 벡터 필드(conservative vector fields)를 형성하지 않습니다(Salimans & Ho, 2021). 따라서, 우리의 분류기-자유 지도 샘플러는 분류기 그라디언트와 전혀 닮지 않은 단계 방향을 따르므로, 분류기에 대한 그라디언트 기반의 적대적 공격(adversarial attack)으로 해석될 수 없으며, 따라서 우리의 결과는 순수 생성 모델과 분류기 그라디언트를 사용하는 이미지 분류기에 대한 적대적이지 않은 샘플링 절차로 분류기 기반의 IS와 FID 메트릭을 향상시킬 수 있음을 보여줍니다.

우리는 또한 지도가 작동하는 방식에 대한 직관적인 설명에 도달했습니다: 샘플의 비조건부 가능성(unconditional likelihood)을 감소시키면서 조건부 가능성(conditional likelihood)을 증가시킵니다. 분류기-자유 지도는 부정적인 점수 항으로 비조건부 가능성을 감소시켜 이를 달성하는데, 이는 우리가 알기로는 아직 탐구되지 않았으며 다른 응용 분야에서 사용될 수 있을 것입니다.

여기서 제시된 분류기-자유 지도는 비조건부 모델(unconditional model)의 훈련에 의존하지만, 경우에 따라 이를 피할 수 있습니다. 클래스 분포가 알려져 있고 클래스가 몇 개밖에 없다면, $\sum_{\mathbf{c}} p(\mathbf{x} \mid \mathbf{c}) p(\mathbf{c})=p(\mathbf{x})$를 사용하여 명시적으로 비조건부 점수를 훈련하지 않고도 조건부 점수로부터 비조건부 점수를 얻을 수 있습니다. 물론, 이는 가능한 $\mathbf{c}$의 값만큼 많은 순방향 패스(forward passes)를 필요로 하며, 고차원 조건부(high dimensional conditioning)에 대해서는 비효율적일 것입니다.

분류기 없는 가이던스(classifier-free guidance)의 잠재적인 단점은 샘플링 속도입니다. 일반적으로 분류기는 생성 모델보다 작고 빠를 수 있으므로, 분류기 가이드 샘플링이 분류기 없는 가이던스보다 빠를 수 있습니다. 왜냐하면 후자는 조건부 점수와 비조건부 점수를 위해 확산 모델(diffusion model)의 두 번의 순방향 패스를 실행해야 하기 때문입니다. 확산 모델을 여러 번 실행해야 하는 필요성은 네트워크 후반부에서 조건을 주입하는 구조로 변경함으로써 완화될 수 있지만, 이러한 탐색은 미래의 연구로 남겨두겠습니다.

마지막으로, 샘플의 충실도를 높이는 대가로 다양성을 희생하는 모든 가이던스 방법은 감소된 다양성이 받아들여질 수 있는지에 대한 질문에 직면해야 합니다. 특정 데이터 부분이 나머지 데이터 맥락에서 대표성이 부족한 응용 분야에서 샘플 다양성을 유지하는 것이 중요하기 때문에, 배포된 모델에서 부정적인 영향이 있을 수 있습니다. 샘플 품질을 향상시키면서 샘플 다양성을 유지하는 방법을 시도하는 것은 흥미로운 미래 연구 분야가 될 것입니다.

6 결론

우리는 확산 모델(diffusion models)에서 샘플 품질을 향상시키면서 샘플 다양성을 감소시키는 방법으로 분류기 없는 가이던스(classifier-free guidance)를 제시했습니다. 분류기 없는 가이던스는 분류기 없이 분류기 가이던스로 생각할 수 있으며, 분류기 없는 가이던스의 효과성을 보여주는 우리의 결과는 순수 생성 확산 모델이 분류기 기반 샘플 품질 메트릭을 최대화할 수 있으며 분류기 그래디언트를 전혀 사용하지 않고도 이를 달성할 수 있음을 확인시켜줍니다. 우리는 더 다양한 환경과 데이터 모달리티에서 분류기 없는 가이던스의 추가적인 탐색을 기대합니다.

7 감사의 말

우리는 토론에 참여해준 Ben Poole과 Mohammad Norouzi에게 감사를 표합니다.

참고 문헌

(a) 비지도 조건부 샘플링(Non-guided conditional sampling): FID=1.80, IS=53.71
(b) 분류기 없는 가이드(Classifier-free guidance) $w=1.0$ : $\mathrm{FID}=12.6, \mathrm{IS}=170.1$
(c) 분류기 없는 가이던스(classifier-free guidance) $w=3.0: \mathrm{FID}=24.83$, IS=250.4

그림 6: ImageNet 64x64에서의 분류기 없는 가이던스. 왼쪽: 무작위 클래스. 오른쪽: 단일 클래스(말라뮤트). 각 부분 그림에서 샘플링을 위해 동일한 무작위 시드가 사용되었습니다.

(a) 가이드 없는 조건부 샘플링(non-guided conditional sampling): FID=7.27, IS=82.45
(b) 분류기 없는 가이던스 $w=1.0$: FID=7.86, IS=297.98
(c) 분류기 없는 가이던스 $w=4.0$: FID=21.53, IS=421.03

그림 7: ImageNet 128x128에서의 분류기 없는 가이던스. 왼쪽: 무작위 클래스. 오른쪽: 단일 클래스(말라뮤트). 각 부분 그림에서 샘플링을 위해 동일한 무작위 시드가 사용되었습니다.

그림 8: 128x128 ImageNet에서의 분류기 없는 가이던스의 추가 예시들. 왼쪽: 가이드 없는 샘플, 오른쪽: $w=3.0$으로 가이드된 분류기 없는 샘플.