Going Deeper with Convolutions(InceptionV1) - 논문 구현

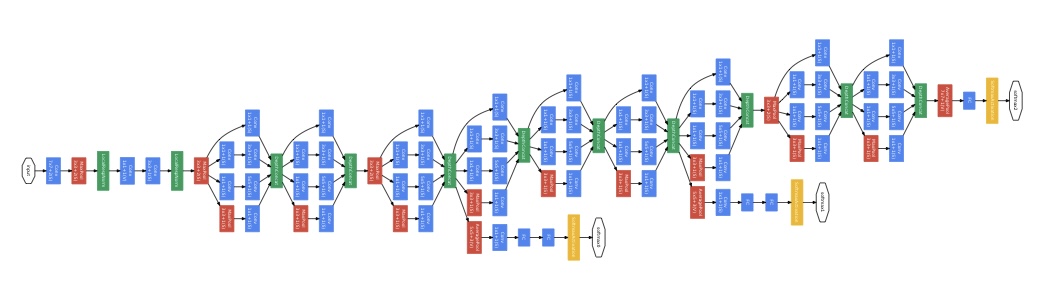
이번 포스팅에서는 GoogLeNet(Inceptionv1) 논문을 정리해보려고 한다.

1. Abstract

이 논문의 초록에서는 GoogLeNet에 대해 간략히 설명하고 있다.
GoogLeNet의 가장 중요한 특징은 연산을 하기 위해 소모되는 자원의 사용 효율이 개선되었다는 것이다. 이것은 네트워크의 깊이와 너비가 증가할 때 연산량은 동일하게 유지함으로써 가능한 것이었다. 또한, 성능의 최적화를 위해 Hebbian Principle과 multi-scale processing을 적용했다.

1-1. Hebbian Principle

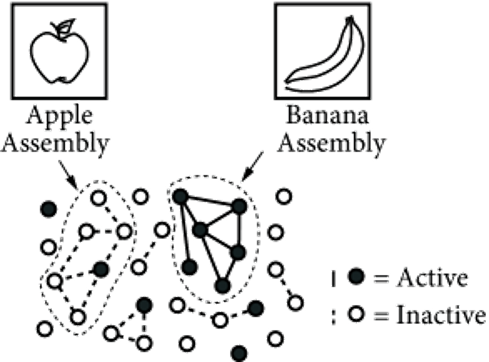
Hebbian Principle은 뇌 이론가인 도날드 헤브 박사가 제안한 이론이다. Hebbian principle 은 “Neurons That Fire Together Wire Together”, 즉 하나의 뉴런이 활성화될때 다른 관련된 뉴런도 활성화됨을 의미한다. 여기서 얻은 직관으로 모든 뉴런을 densly 하게 연결할게 아니라, 연관성이 높은 뉴런들을 sparsely 하게 연결하는 구조를 생각해냈다.

2. Introduction

지난 3년동안, 딥러닝의 발전으로 인해 CNN 분야가 빠른 속도로 성장했다. CNN 분야의 성장은 하드웨어의 성능, 더 큰 데이터셋, 더 큰 모델이 아닌, 새로운 아이디어, 알고리즘, 그리고 개선된 신경망 덕분이었다.
GoogLeNet은 AlexNet보다 12배 적은 파라미터를 사용하는데도 불구하고 더 높은 정확도를 보인다. 이것은 R-CNN과 같이 깊은 모델과 클래식한 컴퓨터 비전의 시너지로 인해 가능했다.

모바일과 임베디드 컴퓨팅에서 전력과 메모리 사용에 대한 알고리즘의 효율성을 중요하게 여겼다. 그래서 모델이 엄격한 고정된 구조를 가지는 것보다 유연한 구조를 가지게 하였다.또한, 연산량을 1.5 billion 이하로 유지하여 본 논문의 내용이 학술적인 호기심으로만 남겨지지 않고 실제 사용될 수 있도록 하였다.

3. Related Work

LeNet-5부터 CNN의 표준 구조가 만들어졌는데, 이는 여러 개의 convolutional layer들, 그리고 그 뒤로 하나 또는 여러개의 Fully Connected layer로 구성된다. 또한, Imagenet과 같은 큰 데이터셋에서의 트렌드가 레이어의 수와 사이즈를 늘리고 dropout을 적용하는 것이기 때문에 GoogLeNet에서도 동일하게 적용했다.

Network-in-Network는 신경망의 표현 능력을 향상시키기 위한 방법이며, 1x1 convolutional layer을 추가하고, 그 후에 ReLU 활성화함수를 사용함으로써 적용시킬 수 있다. 본 논문의 GoogLeNet에서도 이 방법을 사용하며, 그 이유로 2가지가 있다.

1. computational bottleneck를 제거하기 위한 차원 축소
2. 성능의 심각한 저하 없이 네트워크의 깊이와 너비 증가

4. Motivation and High Level Considerations

깊은 신경망의 성능을 향상시키는 방법은 두 가지가 있다.

1. 깊이의 증가(층의 개수)
2. 너비의 증가(각 층의 유닛 개수)

그러나 위의 두 방법들에는 두 가지의 문제점이 존재한다.

1. 오버피팅에 취약해진다.
   더 큰 사이즈는 더 많은 파라마미터의 수를 의미하며, 이는 곧 네트워크가 오버피팅에 취약해진다는 것을 의미한다. 특히 학습 데이터의 수가 적을 경우 더욱 잘 나타난다. 고품질 데이터셋을 만들어내는 것은 어렵고 비용이 많이 들기 때문에 주요 병목현상이 될 수 있다.

2. 컴퓨터 자원의 사용량이 늘어난다.
   예를 들어, 만약 두개의 convolutional layer이 연결되어있다면, 필터 수를 증가시킬 때 연산량은 quadric하게 증가된다. 컴퓨팅 자원은 한정적이기 때문에 무분별하게 네트워크의 크기를 늘리는 것보다 효율적으로 컴퓨팅 자원을 분배하는 것이 중요하다.

위의 두 문제를 모두 해결할 근본적인 방법은 fully connected layer을 sparsely connected layer으로 변경하는 것이다. 만약 크고, 깊고, sparse한 신경망에 의해 데이터셋의 분포 확률을 표현할 수 있다면, 최적의 네트워크는 마지막 layer의 activation의 correlation statistics를 분석하고 highly correlated output으로 묶으면서 구성할 수 있다고 한다.

그러나 오늘날의 컴퓨팅 환경은 균일하지 않은 sparse한 데이터 구조에서 수학적 연산을 할 때 매우 비효율적이다. Dense한 데이터의 연산의 경우, 지속적으로 개선되고 고도로 조정된 수치적인 라이브러리, 그리고 CPU와 GPU의 활용으로 더욱 빨라짐으로써 두 데이터 형식간의 간격은 더욱 커졌다. 그래서 본 논문에서는 sparse matrices를 비교적 dense한 submatices로 클러스터링하여 실용적으로 sparse matrix 연산을 수행하도록 한다.

Inception 구조는 컴퓨터 비전 네트워크에서 sparse한 구조를 사용 가능가능한 component로 구현해보자는 case study에서 시작했다.

5. Architectural Details

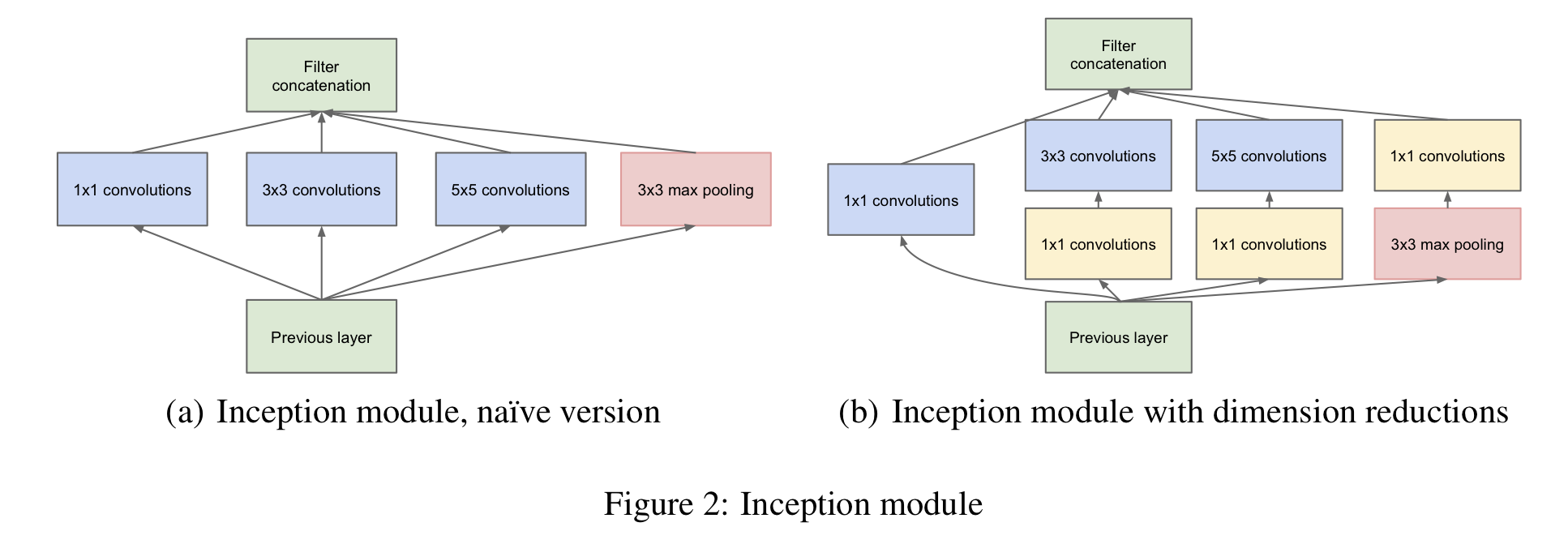
Inception 구조의 주요 아이디어는 CNN 에서 각 요소를 최적의 local sparse structure 으로 근사화하고, 이를 dense component 로 바꾸는 방법을 찾는 것이다. 즉, 최적의 local 구성 요소를 찾고 이를 공간적으로 반복하면 되는 것이다. 이는 Sparse Matrix 를 서로 클러스터링하여 상대적으로 Dense한 Submatrix 를 만듦으로서 가능하다.
본 논문의 Inception에서는 편의를 위해 필터 사이즈를 1x1, 3x3, 5x5로 크기를 제한했다. 이러한 layer들이 모여 다음 stage의 input이 된다. 1x1, 3x3, 5x5 Convolutional filter의 수는 신경망이 깊어짐에 따라 달라지는데, 높은 layer(output에 가까운 layer)에서만 포착될 수 있는 높은 추상적 개념의 특징이 있다면, 공간적 집중도가 감소한다. 따라서 높은 layer를 향해 네트워크가 깊어짐에 따라 3x3과 5x5 Convolutional filter의 수도 늘어나야 하며, 이때 연산량의 수가 늘어난다. 또한, pooling layer의 output을 다른 layer의 output과 concatenate을 할 때 연산량이 더욱 커지는 문제가 발생한다.

이 문제를 해결하기 위해 본 논문에서는 1x1 convolutional layer을 이용한다. 이를 1x1 convolutional layer을 제외한 다른 convolutional layer 앞에, 그리고 pooling layer 뒤에 사용하여 차원을 축소하여 궁극적으로 연산량을 감소시킨다.

본 논문은 메모리를 효율적으로 사용하기 위해 낮은 layer에서는 기본적인 CNN layer을 사용하고, 높은 layer에서는 Inception Module을 사용하는 것을 추천한다.

이와 같은 Inception Module을 사용하면 크게 두 효과를 볼 수 있다.

1. 과도한 연산량의 증가 없이 각 단계에서 유닛 수를 증가시킬 수 있다.
2. 다양한 scale로 처리된 시각 정보를 동시에 학습 가능하다.

5-1. 1x1 Computations

1x1 convolution의 사용여부는 연산량에 매우 큰 영향을 미친다.
먼저, 1x1 convolution을 사용하지 않은 경우의 연산량을 계산해보자.

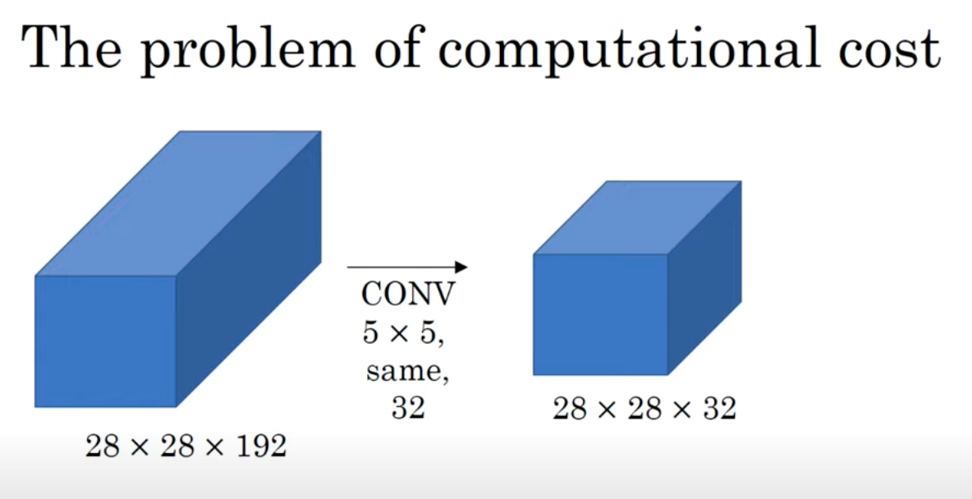
(28x28x32) x (5x5x192)의 결과, 120M이라는 매우 큰 연산량이 나온다.

다음으로, 1x1 convolution을 사용한 경우의 연산량을 계산해보자.

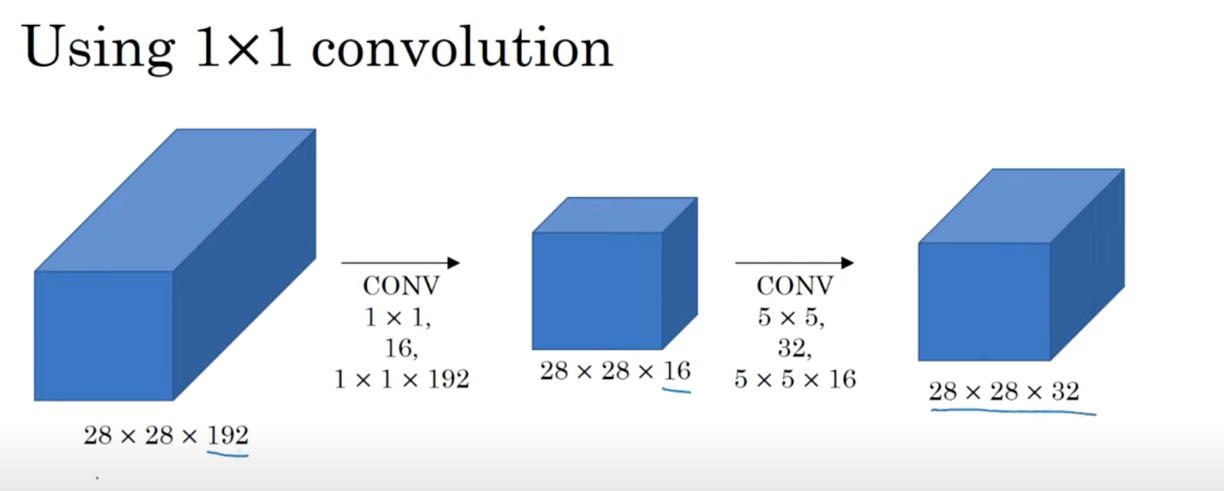
((28x28x16) x (1x1x192)) + ((28x28x32) x (5x5x16))의 결과, 12.4M이라는 연산량이 도출된다.

이를 통해 1x1 convolution을 사용할 경우, 연산량이 매우 크게 줄어든다는 것을 확인할 수 있다.

6. GoogLeNet

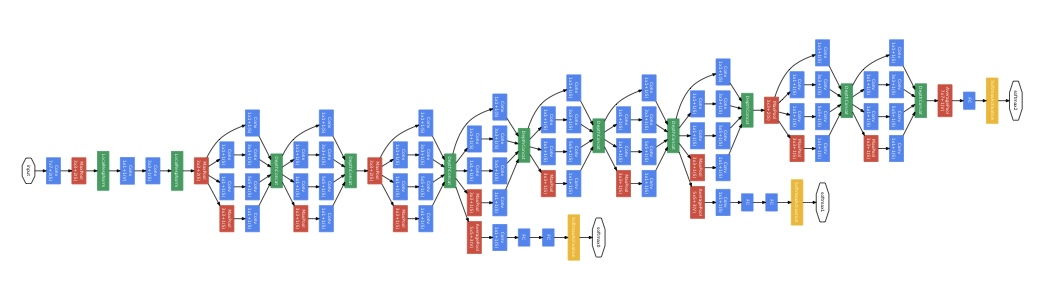
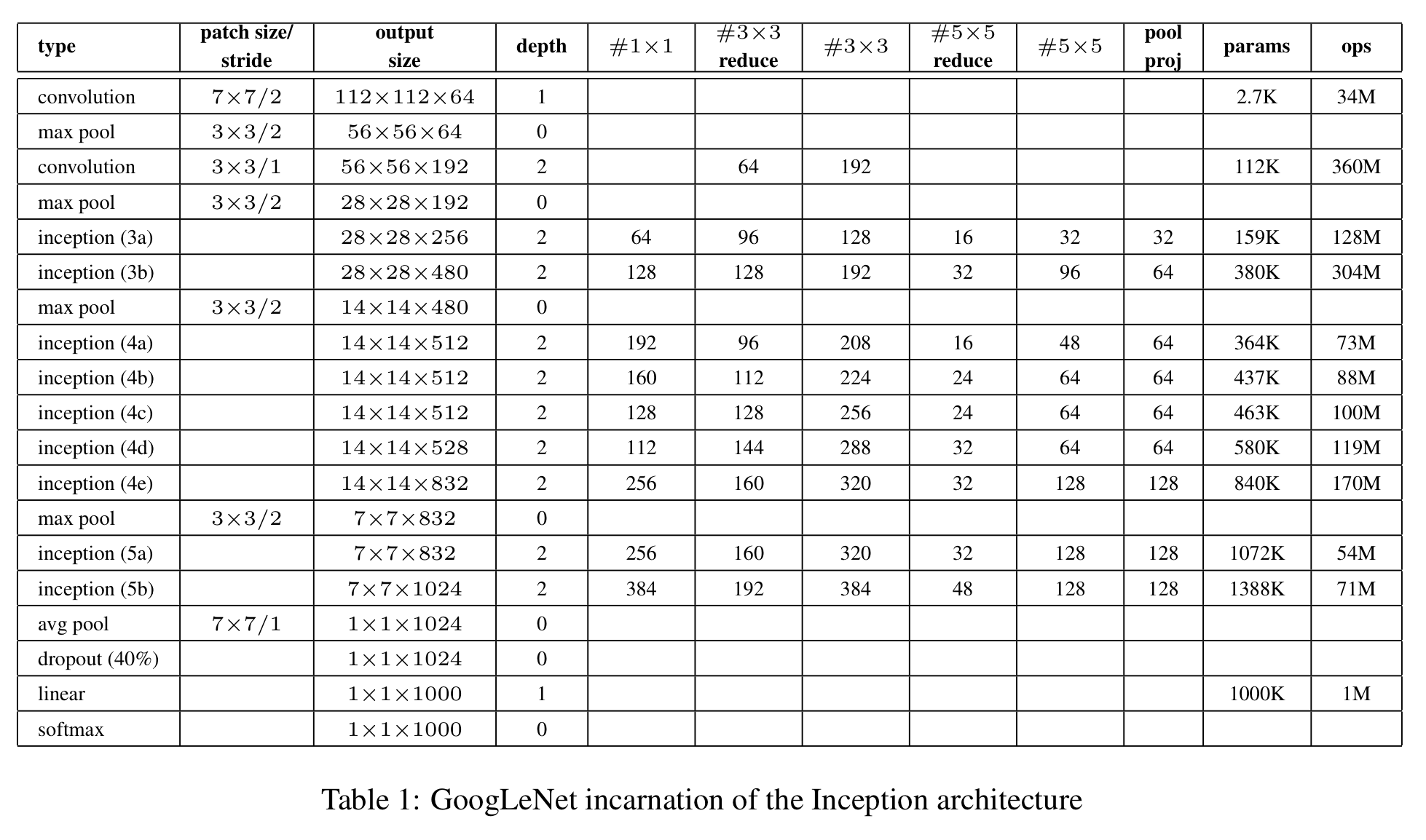
모든 convolution layer에서 ReLU 활성화 함수를 사용한다. 본 모델의 입력은 224x224 mean-subtracted RGB 이미지이다.

네트워크가 깊어지면서, gradient를 효율적으로 역전파시키는 것이 중요해졌다. 그래서 GoogLeNet에서는 auxiliary classifier를 network의 Inceptaion 4a와 Inception 4d 뒤에 추가했다. 학습중에는 auxiliary classifier의 출력의 0.3을 곱해서 전체 loss에 더해지고, 테스트 시에는 auxiliary classifier를 사용하지 않는다.

Auxiliary Classifier은 아래와 같이 구성되었다.

• Inception 4a와 Inception 4d 뒤에 5x5, stride 3인 average pooling
• 필터의 수가 128인 1x1 conv layer 및 ReLU
• 유닛의 개수가 1024개인 fc layer 및 ReLU
• p=0.7의 dropout
• 유닛의 개수가 1000개인 fc layer

논문 구현

import

from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Dense, Conv2D, Dropout, Flatten, Activation, MaxPooling2D, GlobalAveragePooling2D, AveragePooling2D
from tensorflow.keras.optimizers import Adam, RMSprop
from tensorflow.keras.layers import BatchNormalization
from tensorflow.keras.callbacks import ReduceLROnPlateau, EarlyStopping, ModelCheckpoint, LearningRateScheduler

from tensorflow.keras.layers import Concatenate

Inception Module

def inception_module(x, filters_1x1, filters_3x3_reduce, filters_3x3, filters_5x5_reduce, filters_5x5, filters_pool, name=None):

  #1x1 convolutions
  conv_1x1 = Conv2D(filters_1x1, (1, 1), padding = 'same', activation = 'relu')(x)

  #3x3 convolutions
  conv_3x3 = Conv2D(filters_3x3_reduce, (1, 1), padding = 'same', activation = 'relu')(x)
  conv_3x3 = Conv2D(filters_3x3, (3, 3), padding = 'same', activation = 'relu')(conv_3x3)

  #5x5 convolutions
  conv_5x5 = Conv2D(filters_5x5_reduce, (1, 1), padding = 'same', activation = 'relu')(x)
  conv_5x5 = Conv2D(filters_5x5, (5, 5), padding = 'same', activation = 'relu')(conv_5x5)

  #max pooling
  pooling = MaxPooling2D((3, 3), strides = (1, 1), padding = 'same')(x)
  pooling = Conv2D(filters_pool, (1, 1), padding = 'same', activation = 'relu')(pooling)

  output = Concatenate(axis = -1, name=name)([conv_1x1, conv_3x3, conv_5x5, pooling])

  return output

Auxiliary Classifier

def auxiliary_learning(x, fois):
  x = AveragePooling2D((5, 5), strides=3, name='avg_pool'+str(fois))(x)
  x = Conv2D(128, (1, 1), padding='same', activation='relu', name='a_conv'+str(fois))(x)
  x = Flatten()(x)
  x = Dense(1024, activation='relu', name='a_dense'+str(fois))(x)
  x = Dropout(0.7)(x)
  x = Dense(10, activation='softmax', name='softmax_output'+str(fois))(x)

  return x

Inception

def inception(in_shape = (224, 224, 3), n_classes=10):
  input_tensor = Input(in_shape)

  x = Conv2D(64, (7, 7), strides = (2, 2), activation = 'relu', name = 'conv1_7x7/2')(input_tensor)
  x = MaxPooling2D((3, 3), strides = 2, padding = 'same', name = 'max_pool_1_3x3/2')(x)
  x = Conv2D(64, (1, 1), strides = 1, activation = 'relu', name = 'conv2a_3x3/1')(x)
  x = Conv2D(192, (1, 1), strides = 1, activation = 'relu', name = 'conv2b_3x3/1')(x)
  x = MaxPooling2D((3, 3), strides = 2, padding = 'same', name = 'max_pool_2_3x3/2')(x)
  
  #inception_3
  x = inception_module(x, 64, 96, 128, 16, 32, 32, name='inception_3a')
  x = inception_module(x, 128, 128, 192, 32, 96, 64, name = 'inception_3b')
  x = MaxPooling2D((3, 3), strides = 2, padding = 'same', name = 'max_pool_3_3x3/2')(x)

  #inception_4
  x = inception_module(x, 192, 96, 208, 16, 48, 64, name = 'inception_4a')
  x = inception_module(x, 160, 112, 224, 24, 64, 64, name = 'inception_4b')

  x1 = auxiliary_learning(x, 1)

  x = inception_module(x, 128, 128, 256, 24, 64, 64, name = 'inception_4c')
  x = inception_module(x, 112, 114, 288, 32, 64, 64, name = 'inception_4d')
  x = inception_module(x, 256, 160, 320, 32, 128, 128, name = 'inception_4e')

  x2 = auxiliary_learning(x, 2)

  x = MaxPooling2D((3, 3), strides = 2, padding = 'same', name = 'max_pool_4_3x3/2')(x)

  #inception_5
  x = inception_module(x, 256, 160, 320, 32, 128, 128, name = 'inception_5a')
  x = inception_module(x, 384, 192, 384, 48, 128, 128, name = 'inception_5b')

  x = AveragePooling2D((7, 7), strides = 1, padding = 'same', name = 'ave_pool_7x7')(x)

  x = Dropout(0.5)(x)

  output = Dense(n_classes, activation = 'softmax', name = 'output')(x)

  model = Model(input_tensor, [output, x1, x2], name='inception')
  model.summary()

  return model

Learning

model = inception()

epoch = 25
initial_lrate = 0.01

sgd = SGD(lr=initial_lrate, momentum=0.9, nesterov=False)
lr_sc = LearningRateScheduler(decay, verbose=1)

model.compile(loss=['categorical_crossentropy', 'categorical_crossentropy', 'categorical_crossentropy'],
              loss_weights=[1, 0.3, 0.3], optimizer=sgd, metrics=['accuracy'])

history = model.fit(x_train, [y_train, y_train, y_train], validation_data=(x_valid, [y_valid, y_valid, y_valid]),
                    epochs=epoch, batch_size=20, callbacks=[lr_sc])