- 정규분포
-
가장 일반적으로 발견되는 양방향 대칭의 종 모양(사진 참고)으로 생긴 분포,
수집된 자료의 분포를 근사할 때 대부분 정규분포를 사용한다.
(중심 극한정리에 의해 독립적인 확률 변수들의 평균이 정규분포에 가까워지므로)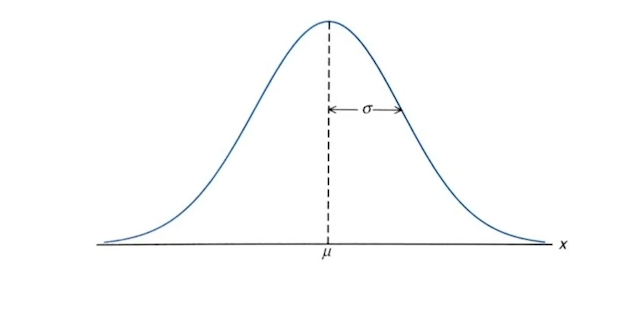
-
모수: μ(평균)과 σ^2(분산)
평균: 분포가 모이는 중심
분산: 평균을 중심으로 데이터들이 퍼진 정도
보통 N(μ, σ^2)로 표현한다.
정규분포가 중요한 이유!
여러 분포들을 정규분포로 근사할 수 있다!
이항분포의 정규분포 근사
이항분포의 pmf에서 n을 무한(극한)으로 보낼 경우 정규분포 근사로 만들 수 있다.
예시)
동전을 던졌을 때 앞이 나오는 경우 X=1 인 확률 변수 X의 경우
X의 시행횟수가 무한대로 늘어날 경우
X의 확률을 히스토그램으로 그리면 N(np, np(1-p))의 분포에 가까워지는 것을 알 수 있다.
이것을 드무아브르-라플라스 정리 라고한다.
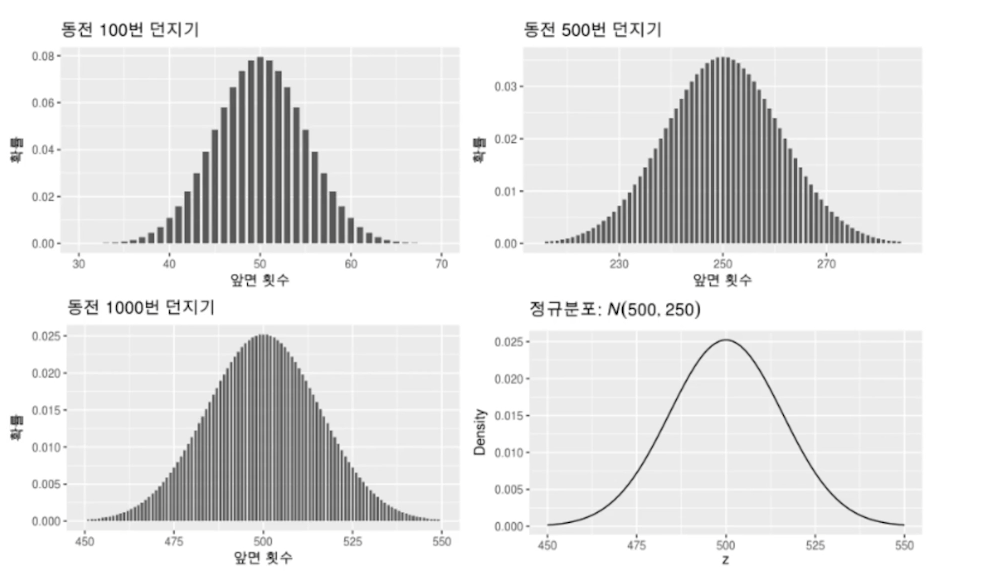
동전을 1000번 던졌을때 앞면횟수가 500(평균)이 중심이 되는 것을 볼 수 있다.
표준 정규 분포
서로 다른 parameter를 가진 집단들을 비교하기 위해 정규분포를 표준화한 분포
즉, 평균이 0이고 퓨준편차가 1인 분포로 표준화
표준 정규분포를 따르는 확률 변수는 z라고 한다.
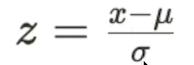
-
표준화된 개별 데이터를 z-score 라고 부르며,
평균으로부터 표준편차의 z배정도 떨어져있다를 의미한다. -
표준 정규분포를 따르는 확률 변수 z 값이
(-2,2)사이에 위치할 확률은 약 95% 이다.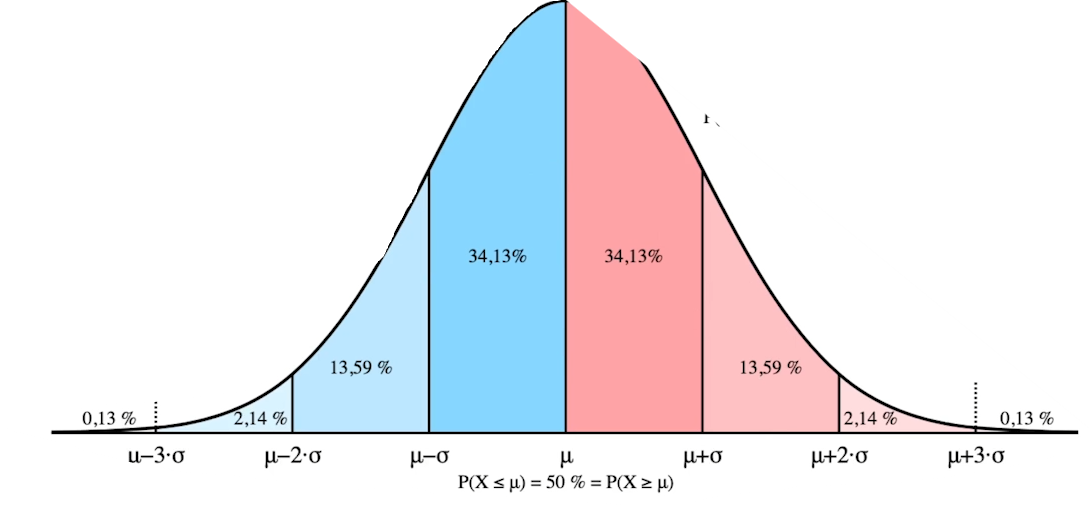
표준 정규 분포표
- 확률 변수 X가 정규분포를 따른다는 가정 하에
표준화를 통해서 z값을 구한 다음
표준 정규 분포표를 이용해 P(Z<z) 확률값을 구할 수 있다. - 예시
-
P(Z<1.96) = 0.975 / 정규분포표에서 1.9와 0.06부분을 찾으면 된다.
P(Z>1.96) = 0.025 / Z가 큰 경우에는 1-1.96을 해주면 된다.
정규분포는 지금까지 배운 듯이 평균값 기준 양쪽 대칭이므로
P(Z<-1.96) = 0.025
따라서
P(-1.96<Z<1.96) = 1- P(Z>1.96) - P(Z<-1.96)
= 0.95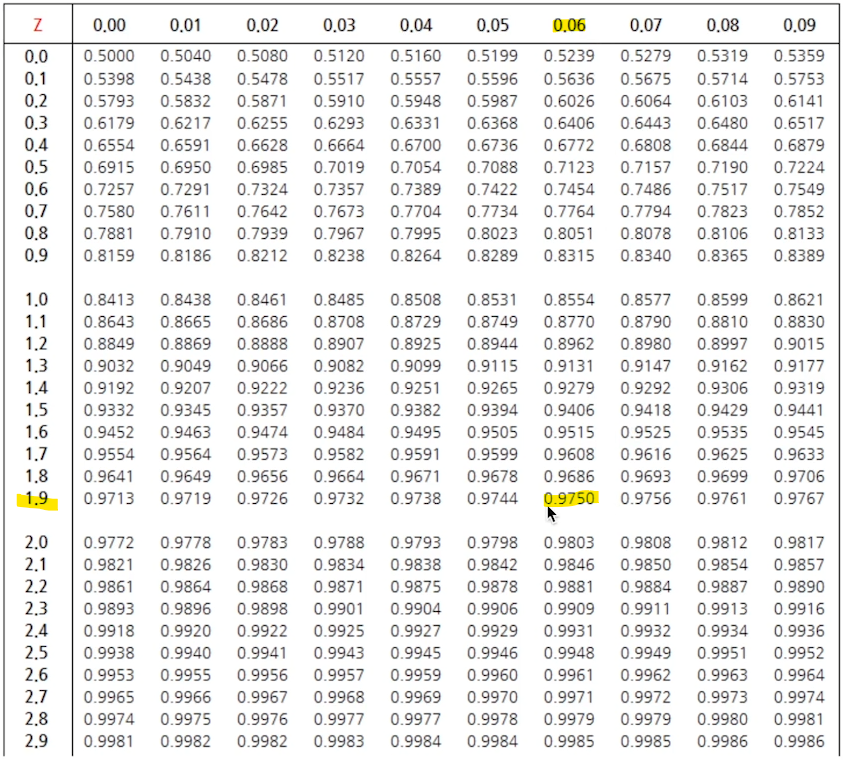
-
표본 평균과 표본 분산
- 모집단으로부터 random sample을 n개 추출했을 때
n개의 random sample들의 평균과 분산을 각각 표본평균/표본분산
단, 이때 random sample들은 i.i.d(무작위 추출 성) 여야 함

Bessel’s correction(불편추정량)
앞에서 표본 분산이 n이 아닌 n-1로 나누는 이유를 확인해 보자
불편추정량이란?
모집단의 모수 추정에 있어서 그것의 추정량의 기댓값이 모수와 같을 때 그 추정량을 가리켜 불편 추정량이라고 한다.
-
추정량 : 모수를 추정하기 위한 표본 통계량
(e.g. 표본평균(모평균을 추청하기 위한 표본 통계량),
표본분산(모분산을 추정하기 위한 표본 통계량)) -
불편향(편향하지 않다) : 표본 추정량의 기댓값이 모수와 같을 때 불편향하다고 함.
- 표본 평균의 엑스바는 뮤가 되는것!(표본평균의 평균은 모평균이 되기 때문)
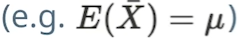
-
왜 표본분산은 n이 아닌 n-1로 나눠주는 걸까?
- n으로 나눠지면 표본분산은 불편추정량이 아니게 되므로 n-1로 나눠주게 된다.(Bessel’s correction)
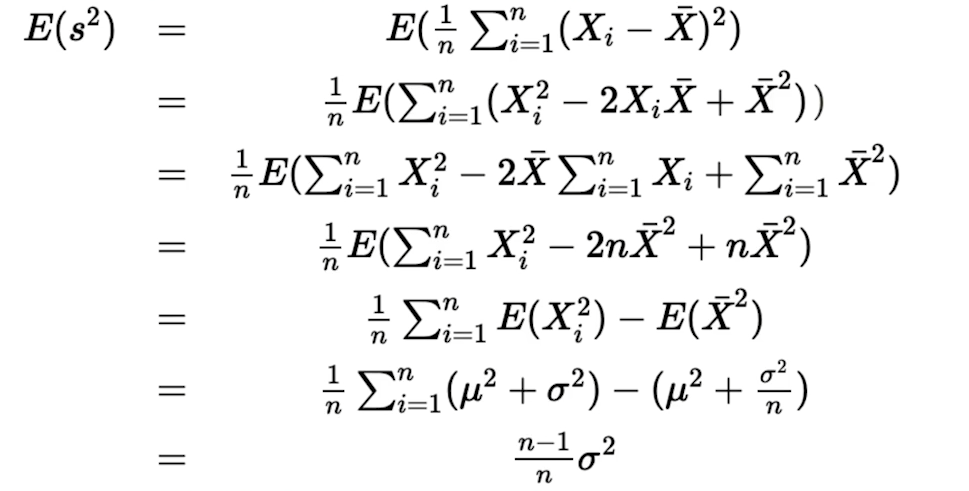
중심극한정리
평균 μ와 분산 σ^2인 임의의 모집단에서 크기가 n인 표본 (X1, …, Xn)을 뽑았다고 했을때
표본 평균의 분포는 n → ∞일때(충분히 클때) N(μ, σ^2/n) 에 근사하고
Z의 분포는 N(0, 1^2)에 근사한다.
그림으로 [중심극한정리]를 설명해 보자면,

Bin(n,P) 라고 할 때 n의 갯수가 무한으로 늘어날 수 록 정규 분포와 근사해진다.
포아송 분포도 마찬가지이다.
2에 중심되는 것을 볼 수 있다.

- 표본들의 합에 대해서도 중심극한정리가 적용된다.
- n개의 표본이 특정 분포를 따르는 것이 아니고,
n개 표본의 평균값이 n → ∞이면 (보통은 n>30 이면 표본들이 정규분포를 따른다고 이야기를 함.)
정규분포를 따르는 것이다.
