[32일차]포아송분포, 균등분포

포아송분포

단위시간/단위공간에서 어떤 사건이 발생하는 횟수를 확률변수 X라 할때, X는 포아송 분포를 따른다고 한다.

• 포아송 분포에서 모수 λ(람다)는 ‘단위시간/단위공간에서의’ 평균 발생 횟수

  • e.g. 1시간 동안 버스가 정류장에 도착하는 횟수

• 포아송 분포의 전제조건

  • 독립성 : 단위 시간/공간에서 발생한 결과는 중복되지 않은 다른 시간/공간에서 발생한 결과와 독립이다.
    • 예시) 8~9시 까지 도착한 버스들과 9~10시까지 도착한 버스들은 서로 독립적이다.
  • 일정성 : 단위 시간/공간에서 발생한 확률/횟수는 그 시간/공간의 크기에 비례한다.
    즉, 단위 시간/공간에서 발생한 평균발생횟수는 일정하다.
    - 예시) 버스가 12~13시에 10대씩 왔다면 13~14시에도 10대식 오는 일정성을 가짐.
  • 비집락성 : 매우 짧은(즉, 같은) 시간/공간에서 두 개 이상의 결과가 동시에 발생할 확률은 0이다.
    • 예시) 8시59분59.111초처럼 엄청 짧은 시간에 버스가 동시에 정류장에 도착할 확률은 0이다.

• 포아송 분포의 pmf

  • e는 자연상수, x!는 1~n을 다 곱한 값

  

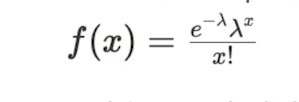
• 포아송 분포의 기댓값과 분산은 모두 λ이다.

  

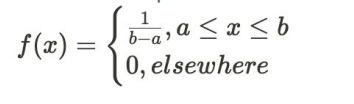
균등분포

모든 확률변수값에 대해 균일한 확률을 갖는 확률 분포

• 구간 [a,b] 내 모든 구간에서 일정한 크기의 확률을 가지는 확률변수 X의 pdf=

  

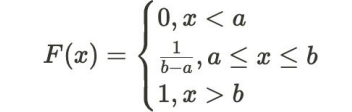
• 모든 확률의 합은 1이므로, 구간 [a,b] 사이의 모든 확률의 합은 1이다.
• 균일분포의 누적분포함수 F(x)=