데이터 모델링을 하는 경우 overfiting(과적합) 되는 경우가 많다.
overfiting(과적합) 이란?
학습데이터에 대해서 과하게 fiting되는 경우를 의미
‘과하게 fiting’ 된다는 의미는 무엇일까?
그 의미를 알기 위해서는 일반화에 대해서 알아야 된다.
Generalization(일반화)
학습할 때와 추론할 때의 성능 차이가 많이 나지 않는 경우.
즉, 모델이 여러 inference 상황에서 잘 쓰일 수 있음을 의미
Overfiting이 발생하는 경우, test set에서의 loss가 증가할 수 있기 때문에 실제 inference 상황에서 모델이 generalization(일반화) 되기 어렵게 된다.
Overfiting은 보통 데이터에 내재된 복잡도 보다 모델의 복잡도가 더 과한 경우나,
데이터 셋 사이즈가 작은 경우 자주 발생된다.
아래 사진에서 N=100 처럼 데이터 셋이 많게되면 Overfiting이 어느정도 해소된다.
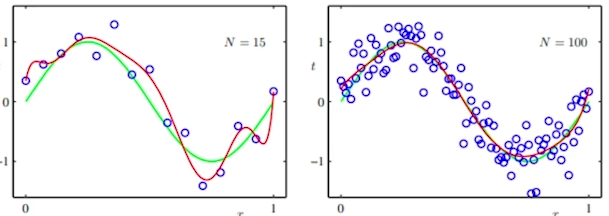
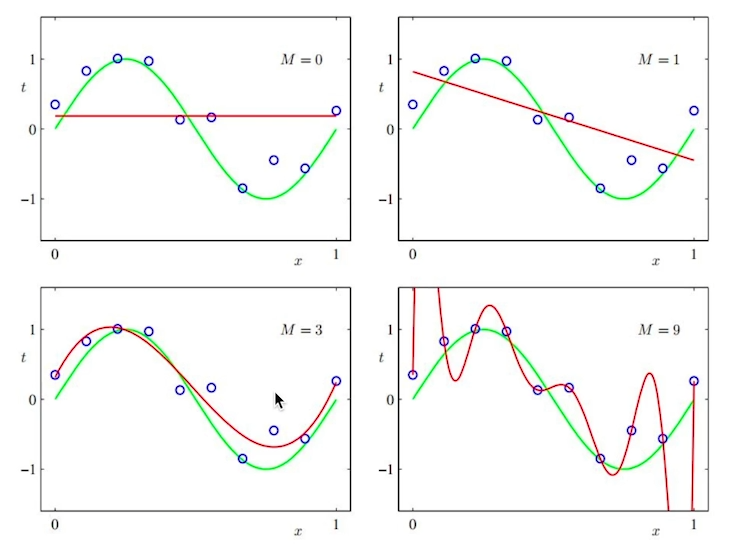
그림을 통해 보자면 M이라는 복잡도가 있다고 하자.
M이 0개일때는 직선, 1개일때는 선형을 따르다가 3개부터 조금씩 로스가 생기더니, 9개가 되자 엄청 어지럽게 된다. 이 상태를 overfitting이라고 한다.
Linear regression(선형회귀)의 경우, 고려하는 변수가 많아질수록 overfitting이 발생할 가능성이 높아진다.
Overfitting 해결법
Overfitting을 해결하는 방법은 크게 두가지다.
- 모델의 복잡도 줄이기
모델이 가질 수 있는 parameter를 줄이거나
(e.g. 딥러닝에서 모델의 사이즈)
모델이 고려하는 feature 중에서
상대적으로 중요한 feature 들만 모델의 input으로 사용. - 정규화(Regularization)
모델이 가지는 복잡도를 제한하는 방법으로
보통 모델의 parameter가 가지는 값의 크기를 cost function에 추가해주는 방식으로
parameter 값의 크기를 제안한다.
Overfitting 해결법- 정규화_Ridge
그렇다면 정규화는 어떤식으로 진행해야 될까?
Ridge regression
-
선형 회귀 모델에 L2 loss를 추가해서 parameter를 정규화 해준다.
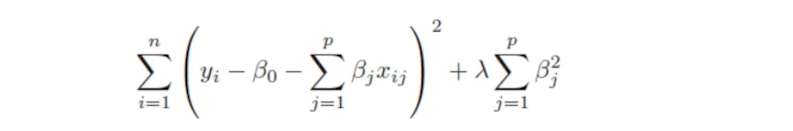
- Ridge regression모델의 패널티항은 모델의
weight parameter들의 제곱합이며,
lambda hyperparameter를 이용해서
모델에 주어지는 패널티를 조절한다.
Ridge regression을 그림으로 설명하자면 아래와 같다.
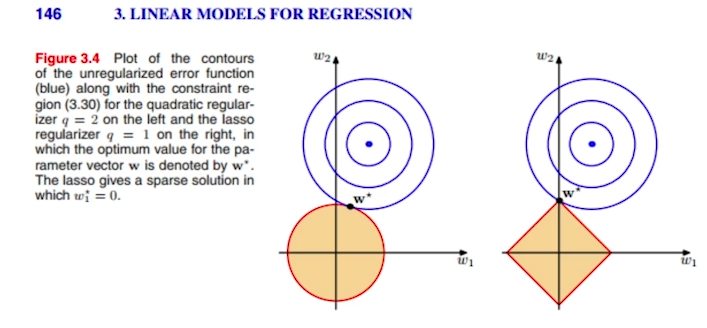
weight들이 가질 수 있는 값이 x축 y축으로 표현되어 있다.
선형회귀를 했을때 cost function이 최저점이 되는 곳은 원의 중심이다.
이때 Ridge regression을 사용하면 weight가 커질 수 있는 제약공간이 만들어진다.(그림에서 원과 마름모.)
최저점에서 값을 점점 넓혀가며 결국 제약공간에 닿는 W* 가 Ridge regression에서 얻을 수 있는 최적화된 parameter이다.
Parameter가 갖는 원형의 제약 조건내에서
cost의 최적점에 가장 가까운 w*를 사용한다.
Overfitting 해결법- 정규화_Lasso
Lasso regression
선형 회귀 모델에 L1 loss를 추가해서 parameter를 정규화 해준다.
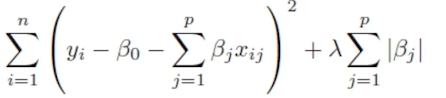
Lasso regression모델의 패널티항은 모델의
weight parameter들의 절대값의 합으로 보면 된다.
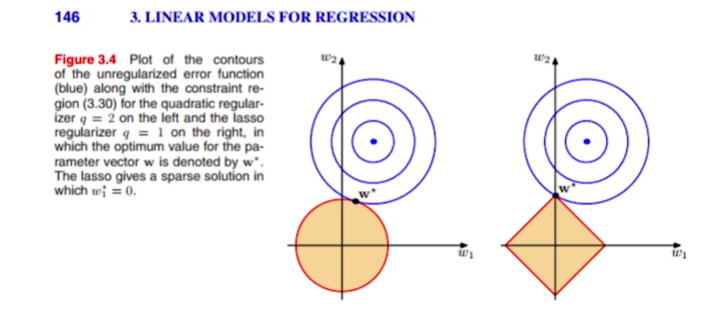
위 사진을 보자
파라미터의 제곱합을 제약조건으로 보면 위처럼 둥굴게 나온다.
하지만 이때 절대값의 합으로 준다면 마름모꼴로 제약조건이 나온다.
(마름모꼴일때)이때 w*가 갖는 x축의 값은 0이된다.(항상 그렇지는 않는다.)
Parameter가 갖는 사각형의 제약 조건 내에서
cost의 최적점에 가장 가까운 w*를 사용하며,
유의미하지 않은 변수들에 대한 계수를 0(중요하지 않은 변수)으로 주어
중요한 변수를 선택할 때 유용하게 사용
가능하다.
