
Neural Networks
- “Neural networks are computing systems vaguely inspired by the biological neural networks that constitute animal brains.”
- 근데 역전파는 인간의 뇌에서 일어나지 않는데..?
- Neural networks are function approximators that stack affine transformations followed by nonlinear transformations.
- 함수를 근사하는 모델. 행렬을 곱하는. 비선형 모델을 연속적으로
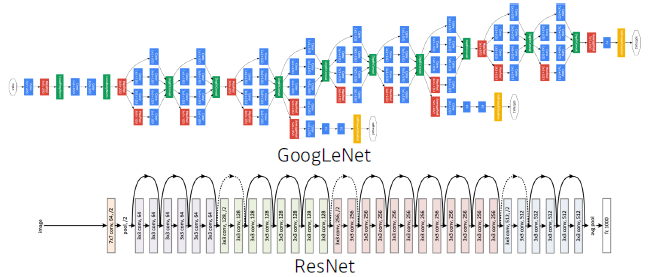
- 함수를 근사하는 모델. 행렬을 곱하는. 비선형 모델을 연속적으로
Linear Neural Networks
-
선형 회귀!
- parameter: 기울기 w, 절편 b
- → 로 가는 mapping function을 찾자
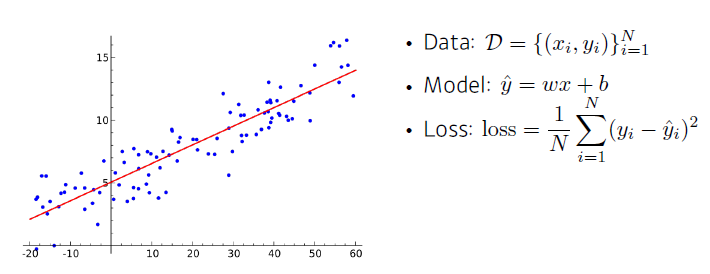
-
We compute the partial derivatives w.r.t. the optimization variables.
- 어떻게 W와 b를 찾을까?
- back-propagation
- loss가 최소화!> parameter가 어느 방향으로 움직였을 때 loss function이 줄어들까?
- loss function을 각각 parameter로 미분, 방향을 역수(음수) 방향으로 update

- loss function을 에 대해 편미분한 값을 찾아 현재 에 편미분 값에 적절한 값을 곱해 빼주어 update
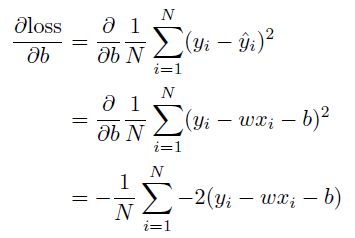
- 에 대해 편미분한 값을 특정 step size만큼 편미분 값에 곱한 다음 빼주어 update
-
Then, we iteratively update the optimization variables.
- 이런 식으로 w와 b를 계속 update해 나가는 방식을 gradient descent라 함
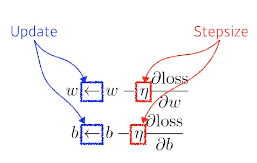
- but 단순히 선형이 아닐 경우,,
- 전체 파라메터로 다 미분하는것: back-propagation
- : stepsize
- 너무 크게되면 학습 x (gradient 정보는 굉장히 local한 정보)
- 0에 가깝게 되면 아에 학습 x
- 이런 식으로 w와 b를 계속 update해 나가는 방식을 gradient descent라 함
-
Of course, we can handle multi dimensional input and output.
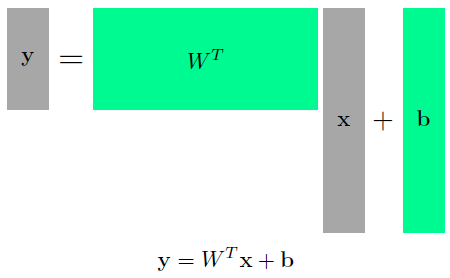
- n차원에서 m차원으로 가는 행렬?
- One way of interpreting a matrix is to regard it as a mapping between two vector spaces.
- 두개의 vector space 사이의 변환
- 와 를 가지고 라는 입력을 라는 출력으로 바꿈
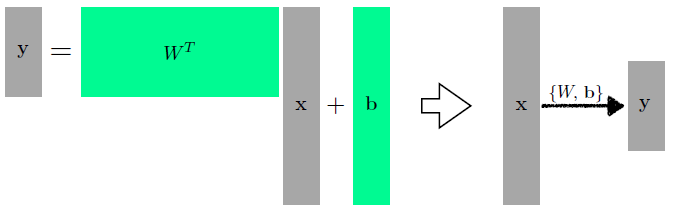
Beyond Linear Neural Networks
- What if we stack more?
- 딥러닝: network를 깊게 쌓겠다!
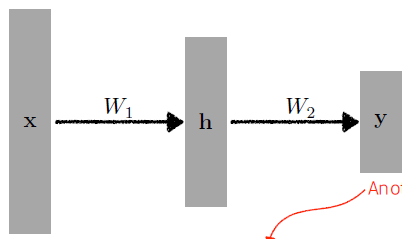
- but 이거는 행렬 두개의 곱에 지나지 않으므로 결국은 한 단짜리 뉴럴네트워크와 다르지 않음
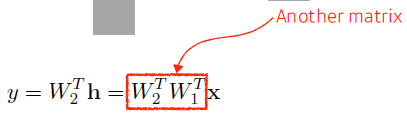
- 딥러닝: network를 깊게 쌓겠다!
- We need nonlinearity.
- (nonlinear transform)가 필요
- mapping(x→y)이 표현할 수 있는 capacity의 극대화를 위해
- 단순히 선형 결합을 n번 반복하는것이 아니라
- 한번 선형 결합이 반복되게 되면 그 뒤에 activation function을 곱해 nonlinear transform을 거치고 그렇게 얻어지는 feature vector를 다시 선형변환을 하고 nonlinear transform을 하는 것을 n번 진행하면 더 많은 표현력을 얻음
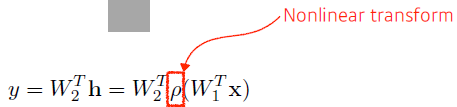
- (nonlinear transform)가 필요
- Activation functions
- 어떤 nonlinear function?
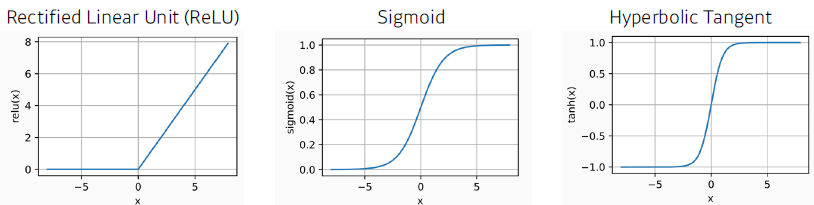
- 어떤 nonlinear function?
- 왜 neural network가 잘 될까?
- There is a single hidden layer feedforward network that approximates any measurable function to any desired degree of accuracy on some compact set K.
- hidden layer가 하나 있는 뉴럴 네트워크는 대부분의 continuous 한 mesurable function을 근사할 수 있다.
- caution: it only guarantees the existence of such networks
- 이것은 존재성만을 보임. 세상 어디엔가 있지만 내가 학습시킨 neural network가 그럴까?
- There is a single hidden layer feedforward network that approximates any measurable function to any desired degree of accuracy on some compact set K.
Multi-Layer Perceptron
- This class of architectures are often called multi-layer perceptrons.
- 입력이 주어져 있고 그 입력을 hidden layer을 거쳐!
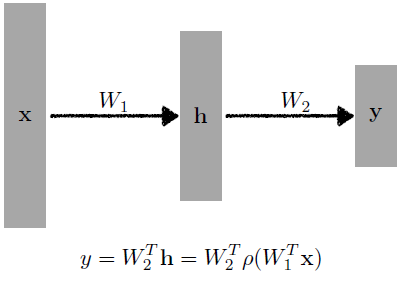
- 입력이 주어져 있고 그 입력을 hidden layer을 거쳐!
- Of course, it can go deeper.
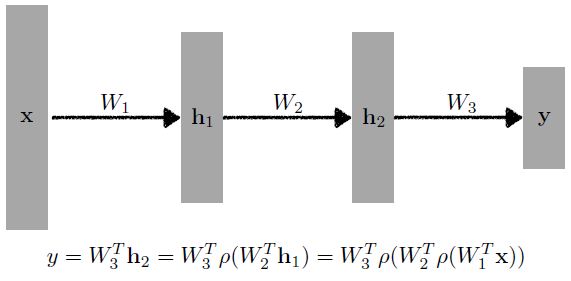
- What about the loss functions?

- 입력이 주어졌을 때 해당 출력값과 데이터셋에서 나오는 target data 사이의 제곱을 줄이는 것(MSE)
- 이것이 항상 우리의 목적을 충족X (학습 데이터에만 맞춤)
- 분류: 다른 값들 대비 높기만 하면 됨!
- 과연 cross entropy가 분류 문제의 loss function으로 최적일까?
- 확률적 모델
- 가우시안 log likelihood를 maximalize하기
- 입력이 주어졌을 때 해당 출력값과 데이터셋에서 나오는 target data 사이의 제곱을 줄이는 것(MSE)
