[Paper Review]Causal Discovery in the Presence of Missing Data

yeorurirurariru·2025년 11월 9일

Paper Review

목록 보기

5/6

결측자료분석 수업의 논문 발표 과제를 위해 읽은 논문

Causal Discovery in the Presence of Missing Data

KTH Royal Institute of Technology, 2Microsoft Research, Cambridge, 3Karolinska Institute, 4University of California, Berkeley, 5Carnegie Mellon University

데이터 항목들이 MCAR이 아닐 경우, 관측된 데이터에서의 독립 관계는 기저 인과 관계에 의해 생성된 완전한 데이터에서의 관계와 다를 수 있음.

단순히 기존의 인과 발견 방법을 이러한 결측이 존재하는 관측 데이터에 그대로 적용하면 잘못된 결론에 도달할 위험이 있다.

목표 : 다양한 결측 매커니즘 아래에서 관측된 데이터로부터 기저 인과 구조를 복원할 수 있는 새로운 인과 발견 방법 개발

결측 메커니즘은 결측 그래프(missingness graph, m-graph)로 표현됨.
완전한 데이터에서의 조건부 독립관계를 도출하기 위해 추가적인 보정이 필요한 조건을 분석
기존 PC 알고리즘을 확장한 MVPC (Missing Value PC) 알고리즘을 제안함.
MVPC는 이러한 추가 보정을 통합함으로써, 데이터가 MAR이나 MNAR인 경우에도 이론적으로 점근적으로 올바른 결과를 산출함을 보인다.

Introduction

의료분야에서 특히 인과관계를 규명하는 일은 중요함
전통적인 접근법 -> 무작위 통제 실험 (randomized controlled trial, RCT)으로 인과 관계를 규명 -> 비용 , 실행 불가능하다는 단점 존재함.
관측 데이터로부터 인과 구조를 탐색하는 방법 점점 폭넓게 활용되고 있다.
기존의 인과 발견 알고리즘 : complete data를 전제로 설계됨. ex) PC algorithm -> 현실적으로는 missing data 흔함.

Missingness Mechanism

1️⃣ MCAR (Missing Completely At Random)
결측이 완전히 무작위로 발생하는 경우이다.
2️⃣ MAR (Missing At Random)
결측이 다른 관측된 변수들에 의해 설명될 수 있는 경우이다.
ex) “성별”과 “소득” 두 변수 중
소득 데이터가 결측되는 확률이 성별에 따라 다르다면, 이는 MAR에 해당한다.
3️⃣ MNAR (Missing Not At Random)
결측이 관측되지 않은 변수 자체에 의해 발생하는 경우이다.
ex) 소득이 낮은 사람일수록 자신의 소득을 기입하지 않을 확률이 높은 경우, 이것은 MNAR이다.

결측이 없는 샘플만으로 분석을 수행할 경우의 문제점
1. 샘플 크기 감소
2. MAR, MNAR 상황에서는 분석 결과를 편향시킨다.

따라서, 결측 데이터가 존재하는 상황에서도 인과 구조를 올바르게 복원할 수 있는 방법을 탐구
결측 메커니즘을 그래프적으로 표현 및 조건부 독립성 관계 분석
결측이 존재해도 유효한 인과 탐색이 가능하도록 함.

PC 알고리즘의 모든 CI 검정을 단순히 교정하는 대신,
어떤 조건에서 CI 검정이 잘못된 간선(erroneous edge) 을 만들어내는지를 규명하고,그러한 간선들만 선택적으로 교정하는 방법을 제안

본 논문의 주요 기여점

1. 결측 메커니즘이 PC 알고리즘 결과에 미치는 오류 영향을 이론적으로 분석

기존의 삭제 기반(deletion-based) 인과 발견 방법(예: PC)이 결측 데이터의 편향(bias) 때문에 어떤 상황에서 잘못된 결과를 초래할 수 있는지를 보인다.
결측 메커니즘이 어떤 경우에만 오류를 야기하는지를 규명 + 그 결과 PC에서 소수의 CI 검정만 교정하면 충분하다는 사실

2. 새로운 보정(correction) 기반 확장 알고리즘,

MVPC (Missing Value PC) 를 제안
MVPC는 기존 PC 알고리즘을 확장하여 세 가지 결측 메커니즘(MCAR, MAR, MNAR) 을 모두 처리 가능함.

3. MVPC는 다양한 환경에서 기존 방법들보다 우수한 성능

합성 데이터(synthetic data) 에 대해 MVPC를 평가
두 가지 실제 의료 데이터셋 — Cognition study와 Achilles Tendon Rupture study — 에도 적용

Causal discovery

① 제약 기반 (PC, FCI)

PC 알고리즘
: 혼란 변수 없다고 가정 CPDAG (Completed Partially Directed Acyclic Graph) 산출
FCI (Fast Causal Inference)
: 혼란변수(confounder) 와 선택 편향(selection bias) 을 허용해서 PAG (Partial Ancestral Graph) 를 산출
인과 마르코프 조건, 신실성 가정 전제
데이터에서의 조건부 독립성을 탐색 -> 인과 구조 복원

② 점수 기반

Greedy Equivalence Search (GES)
- 특정 점수 기준에서 동일한 CI 관계를 가지는 DAG 집합 중 가장 높은 점수를 얻는 Markov 동치류 찾는 것

③ 함수적 인과 모델 기반

데이터의 분포나 함수적 형태에 대한 추가적인 가정을 도입하여 인과 방향을 추정
LiNGAM (linear non-Gaussian model)
PNL (Post-NonLinear) causal model
ANM (Additive Noise Model)

Dealing with data with missing values from a causal perspective.

최근 결측 데이터 문제를 인과적 관점에서 분석하려는 연구가 급격히 늘어나고 있다.
특히 복원 가능성, 검정 가능성의 개념이 활발히 연구
결측 과정을 인과 그래프로 모델링하는 접근에 기반한다.

복원 가능하다(recoverable)
m-graph가 주어졌을 때, 특정 질의(query)
예를 들어 조건부 분포(conditional distribution), 결합 분포(joint distribution),또는 인과 효과(causal effect)가 일관되게 추정될 수 있다면, 그 질의는 복원가능

검정 가능성
“검정 가능한 함의(testable implications)”
즉,결측 데이터 분포에서 실제로 반증 가능한 주장들을 의미

인과 발견
결측 구조 자체보다는 관심 있는 변수들 간의 구조를 찾는 데 초점
특정 가정하에서는 관심 변수들 간 관계 검정 가능, 변수와 그 변수의 결측 여부 간의 관계는 검정 불가능함!!

인과 발견에서, MNAR을 다루는 연구는 많지 않음.
FCI 알고리즘은 결측을 일종의 selection bias로 간주
-> “test-wise deletion” 방식으로 MNAR 결측을 처리
-> 모든 변수를 포함하는 PAG (Partial Ancestral Graph) 추정 시 유효

결측 데이터와 선택 편향은 본질적으로 다르다.

- selection bias
표본이 선택된 데이터의 분포만을 관찰, 모집단 전체의 분포는 알 수 없음.
- 결측 데이터
관측 가능한 데이터로부터 특정 변수들 간의 조건부 독립성을 여전히 확인 가능

(1) 결측 메커니즘이 알려진 경우,

이 문제는 결측 모델의 복원 가능성(recoverability) 과 밀접하게 관련된다.

각 CI 검정마다 Inverse Probability Weight (IPW) 를 적용하여 결측 모델이 알려져 있다고 가정할 때, 이론적으로 결측 보정을 수행할 수 있음을 제안

실제 응용에서 결측 모델을 정확히 알기 어렵기 때문에 현실적이지 않을 수 있다.

(2) 결측 모델이 알려지지 않은 경우,

이들은 가능한 모든 결측 구조를 고려해 가장 드문(sparse) 그래프를 선택하는 방식을 사용했지만, 이는 계산적으로 매우 비효율적.

3. Deletion-based PC: A first proposal and its behavior

관측된 변수 집합에 대해 confounder, selection bias가 존재하지 않는다고 가정.

데이터에 결측값이 포함되어 있을 경우, 결측이 없는 샘플에 대해서만 조건부 독립성 검정 수행 -> 인과 구조 탐색 가능 -> deletion-based PC
결측으로 인해 deletion-based PC의 출력이 잘못될 수 있음.

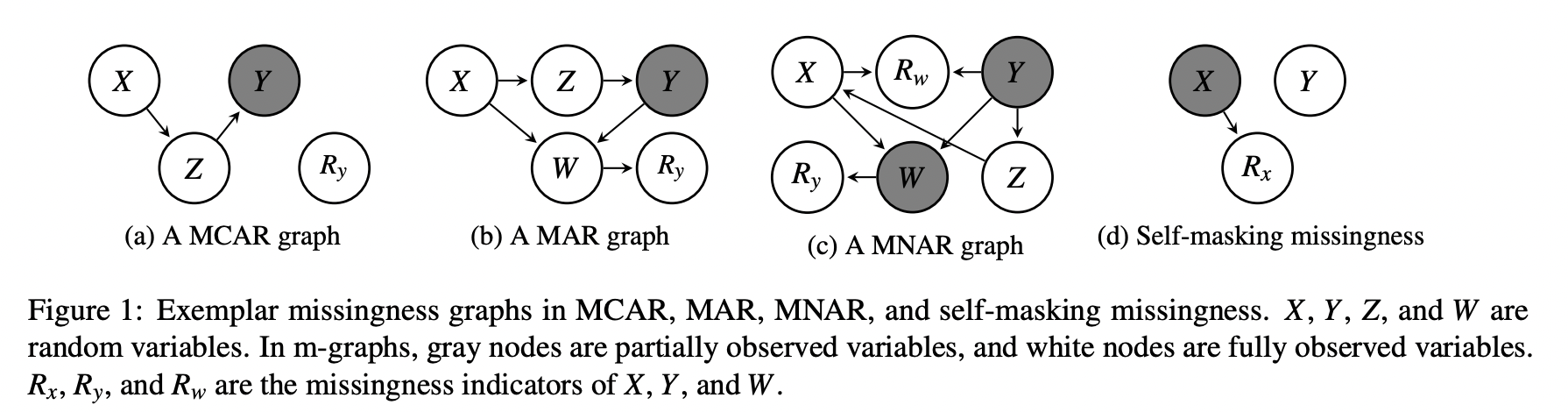
Missingness graph의 정의

m-graph는 인과적 DAG(Directed Acyclic Graph)이며, 다음과 같이 표현된다.

G(V, E)

여기서

V = V_o \cup V_m \cup U \cup R

U: 비관측 변수 집합 (본 논문에서는 인과적 충분성 causal sufficiency 을 가정하므로, $U$ 는 공집합이다.)
Vₒ: 완전하게 관측된 변수 집합 (fully observed variables)
Vₘ: 적어도 한 번 이상 결측된 변수 집합 (partially observed variables)

즉, $V_o$ 와 $V_m$ 은 관측 가능한 변수들 (substantive variables) 의 집합이다.

회색으로 표시된 영역은 $V_m$ 이며,
각 결측 변수에 대해 결측 여부를 나타내는 결측 지표 (missingness indicator) 가 존재한다.
이 지표들은 $R_y, R_x, \ldots$ 등으로 표시된다.

예를 들어, 변수 $Y$ 가 결측되는 경우를 나타내는 변수 $R_y$ 를 도입하면
이는 다음과 같이 정의된다.

R_y = 1 \quad \text{: } Y \text{의 값이 결측(missing)임을 의미}

R_y = 0 \quad \text{: } Y \text{의 값이 관측(observed)되었음을 의미}

결측 시, $Y^*$ 는 $Y$ 의 관측된 값 또는 대체값 (substitute value) 을 의미하며,
이는 유도 과정에서의 편의를 위한 보조 변수 (auxiliary variable) 로 도입된다.

Assumptions for dealing with missingness

기존 PC 알고리즘이 점근적으로 올바르게 작동하기 위한 가정들
(예: 인과 마르코프 조건, 신실성 가정, 비혼란성 등)에 더하여,
결측 데이터를 다루기 위해 아래의 4가지 추가 가정을 도입한다.

Assumption 1 — Missingness indicators are not causes

결측 지표는 원인이 될 수 없다.
No missingness indicator can be the cause of any substantive (observed) variable.

이 가정은 대부분의 m-graph 관련 연구
(Mohan et al., 2013; Mohan and Pearl, 2014a)에서도 동일하게 사용된다.

즉, 관심 변수 $X, Y$ 가 변수 집합 $Z \subseteq V \setminus \{X, Y\}$ 에 의해
d-separation 되지 않는다면,
결측 지표를 함께 포함해도 여전히 d-separation 되지 않는다.

신실성 가정(faithfulness assumption) 하에서는
만약 $X$ 와 $Y$ 가 $Z$ 에 대해 조건부 독립이라면,
결측 지표까지 포함하더라도 여전히 조건부 독립임을 의미한다.

하지만 일반적으로,
결측 지표가 1 (즉, 결측 상태)일 때 해당 변수의 값이 없기 때문에
$Z$ 와 결측 지표를 동시에 고려한 조건부 독립성은 직접 검증할 수 없다.
따라서 다음 가정이 필요하다.

Assumption 2 — Faithful observability

관측 충실성
Any conditional independence relation in the observed data also holds in the unobserved data.

즉, 관측된 데이터에서 성립하는 모든 조건부 독립 관계는
완전한(결측 없는) 데이터에서도 성립한다.

수식으로는 다음과 같다.

X \perp Y \mid \{Z, R_K = 0\} \iff X \perp Y \mid \{Z, R_K = 1\}

여기서

$R_K = \{R_X, R_Y, R_Z\}$ 는 결측 지표 집합이다.
$R_K = 0$ 은 모든 결측 지표가 “관측됨”을 의미하고,
$R_K = 1$ 은 하나 이상의 결측 지표가 “결측됨”을 의미한다.

이로부터 다음이 성립한다.

X \perp Y \mid \{Z, R_K = 0\} \iff X \perp Y \mid \{Z, R_K\}

즉, 관측 데이터에서의 조건부 독립 관계는
완전한 데이터에서도 그대로 유지되며,
결측으로 인해 새로운 독립 관계가 인위적으로 생기지 않는다.

Assumption 3 — No causal interactions between missingness indicators

결측 지표 간에는 인과적 상호작용이 없다.
No missingness indicator can be a deterministic function of any other missingness indicators.

즉, 하나의 결측 지표가
다른 결측 지표에 의해 결정되거나 의존하지 않는다.

Assumption 4 — No self-masking missingness

자기 마스킹(self-masking) 은
변수 자체가 스스로의 결측을 유발하는 경우를 말한다.

수식적으로, m-graph 상에서
이는 $X \to R_X$ 형태의 간선으로 표현된다.

X \to R_X, \quad \text{for } X \in V_m

이 논문에서는 이러한 형태의 간선이 존재하지 않는다고 가정한다.
즉, 어떤 변수도 자신의 결측 여부를 스스로 결정하지 않는다.

정리

번호	가정	설명
1	결측 지표는 원인이 될 수 없음	$R$ 은 실제 변수 $X, Y$ 의 원인이 아님
2	관측 충실성	관측된 독립 관계는 완전한 데이터에서도 유지
3	결측 지표 간 인과 없음	결측 지표들끼리는 결정 관계가 없음
4	자기 마스킹 없음	변수는 자신의 결측을 유발하지 않음

Effect of missing data on the deletion-based PC

결측 데이터가 존재할 때, 리스트 단위 삭제(list-wise deletion) PC 알고리즘은
결측값이 포함된 모든 레코드를 제거하고, 남은 데이터에 대해 PC 알고리즘을 적용한다.

반면, 테스트 단위 삭제(test-wise deletion, TD-PC) 알고리즘은
현재 수행 중인 조건부 독립성 검정(CI test)에 필요한 변수들에 대해서만
결측된 레코드를 삭제한다.
즉, 테스트마다 필요한 변수들만 남겨서 계산하기 때문에
리스트 삭제보다 훨씬 효율적이다 (Strobl et al., 2017).

따라서 본 논문에서는 TD-PC (Test-wise Deletion PC) 알고리즘에 초점을 맞춘다.

TD-PC의 점근적 정확성

TD-PC는 데이터가 MCAR일 때 점근적으로 올바른 결과를 도출한다.

예를 들어, Figure 1a에서

R_y \perp \!\!\! \perp \{X, Y, Z\}

가 성립한다고 하자.
이 경우,

X \perp \!\!\! \perp Y \mid Z \iff X \perp \!\!\! \perp Y \mid \{Z, R_y\}

가 된다.

Faithful observability (가정 2) 하에서는
다음이 성립한다:

X \perp \!\!\! \perp Y \mid Z \iff X \perp \!\!\! \perp Y^* \mid \{Z, R_y = 0\}

따라서,
테스트 단위 삭제된 데이터(즉, 결측 없는 관측치들)에서 수행한 CI 검정 결과는
MCAR 데이터의 경우 올바른 d-separation 관계를 보장한다.
즉, TD-PC는 MCAR 하에서 점근적으로 정확하다.

MAR/MNAR 상황에서의 문제점

하지만 데이터가 MAR 또는 MNAR일 경우,
TD-PC는 잘못된 간선(extraneous edges) 을 생성할 수 있다.

특히, $\{V_m, V_o\} \not\!\perp\!\!\!\perp R$ 인 상황에서는
결측과 관련된 의존성이 생기기 때문에
관측된 데이터만으로는 실제 독립성을 완벽히 반영하지 못한다.

따라서, 이후 절에서는
TD-PC가 어떤 조건에서 오류 간선을 생성하는지를 분석한다.

Erroneous edges produced by TD-PC

TD-PC는 MAR 또는 MNAR 상황에서 잘못된 간선을 만들 수 있다.
이에 대한 수학적 증명은 부록(Appendix A.2)에 제시되어 있다.

우선, TD-PC로 얻은 causal skeleton(비방향 그래프)은
결측 간선은 포함하지 않지만,
불필요한 추가 간선(extraneous edges) 을 포함할 수 있다.

이 절에서는
TD-PC 결과에 잘못된 간선이 포함되는 조건을 제시한다.

Proposition 1

Under Assumptions 1–4,
the CI relation in test-wise deleted data
$X \perp \!\!\! \perp Y \mid \{Z, R_X = 0, R_Y = 0, R_Z = 0\}$
implies the CI relation in complete data
$X \perp \!\!\! \perp Y \mid Z$
where $X, Y$ are random variables and $Z \subseteq V \setminus \{X, Y\}$ .

즉, 테스트 단위 삭제 데이터에서 조건부 독립으로 나타나면
완전한 데이터에서도 독립이 성립한다.

하지만 반대로,
삭제된 데이터에서의 의존 관계가 실제로는
결측 지표에 의해 유발된 허위 의존성(false dependence) 일 수 있다.

예를 들어 Figure 1b에서,
TD-PC는 다음 관계를 잘못 해석한다:

X \not\!\perp\!\!\!\perp Y^* \mid \{Z, R_y = 0\}

하지만 실제로는

X \perp\!\!\!\perp Y \mid Z

가 성립한다.
즉, TD-PC는 결측 지표로 인해 $X$ 와 $Y$ 간의 거짓 간선을 만들어낸다.

Proposition 2

Suppose that $X$ and $Y$ are not adjacent in the true causal graph,
and that for any variable set $Z \subset V \setminus \{X, Y\}$ ,
$X \perp\!\!\!\perp Y \mid Z$ holds.

Then, under Assumptions 1–4,
extraneous edges appear in TD-PC if
there exists a variable $W \in \{X, Y\} \cup \text{descendants}$
whose missingness indicator $R_W$ is a direct cause or descendant of the direct common effect of $X$ and $Y$ .

즉,
$X$ 와 $Y$ 가 실제 인과 그래프에서는 인접하지 않더라도,
결측 지표가 $X$ 와 $Y$ 의 공통 효과(common effect)의 자식(descendant) 인 경우
TD-PC는 잘못된 간선을 생성하게 된다.

요약

구분	내용
MCAR	TD-PC는 올바른 인과 구조를 복원 (점근적 정확성 보장)
MAR / MNAR	결측 메커니즘과 변수 간 의존성으로 인해 잘못된 간선 발생 가능
Proposition 1	테스트 단위 삭제에서 독립이면 완전 데이터에서도 독립
Proposition 2	결측 지표가 공통효과의 자식일 경우, TD-PC는 오류 간선 생성

4 Proposed method: Missing-value PC

4.1 Overview of MVPC

Permutation-based Correction (PermC)

이 절에서는 PermC (Permutation-based Correction) 를 사용하여
TD-PC가 만들어내는 불필요한 간선(extraneous edges)을 제거하는 방법을 설명한다.

문제 상황

예를 들어, Figure 1b에서처럼
결측을 포함한 데이터셋 $(X, Y, Z)$ 가 있다고 하자.
이때 TD-PC를 적용하면 $X$ 와 $Y$ 사이에 가짜 간선이 생성될 수 있다.

그 이유는, TD-PC가 실제 결합 분포 $P(X, Y, Z)$ 대신
결측이 없는 부분 데이터 $P(X, Y^*, Z \mid R_y = 0)$ 를 이용하기 때문이다.

즉, 조건부 독립성 검정이 왜곡되어
결과적으로 불필요한 간선(extraneous edge) 이 생기게 된다.

PermC의 핵심 아이디어

PermC는 이러한 문제를 해결하기 위해
결측 원인 변수 $W$ 를 도입하고,
결측이 없는 상태의 가상 데이터(virtual dataset) 를 재구성한다.

먼저 결합 분포는 다음과 같이 표현된다:

P(X, Y, Z) = \int_W P(X, Y, Z \mid W) P(W) \, dW = \int_W P(X, Y^*, Z \mid W, R_y = 0) P(W) \, dW \tag{1}

여기서:

$W$ : 결측 지표 $R_y$ 의 직접 원인(direct cause)
$Y^*$ : 결측을 포함한 $Y$ 의 관측값 (missing일 수도 있음)

PermC의 작동 원리

1️⃣ $W$ 학습

관측된 결측 없는 데이터( $R_y=0$ )에서
$P(X, Y, Z \mid W, R_y=0)$ 을 회귀 모델로 학습한다.

2️⃣ $W$ 재표본화 (sampling)

$P(W)$ 에서 새로운 샘플을 생성한다.
(이는 결측 원인의 분포를 반영하는 가상 데이터 생성 단계다.)

3️⃣ 가상 데이터 생성

학습된 모델을 이용해 $(X, Y, Z)$ 의 가상 데이터를 복원한다.
이 데이터는 실제 $P(X, Y, Z)$ 와 동일한 분포를 따르도록 설계된다.

4️⃣ 조건부 독립성(CI) 검정

복원된 가상 데이터에서 $X, Y, Z$ 의 독립성을 검정한다.
→ 결측의 영향을 제거한 “진짜 인과 관계”만 남는다.

수식적 설명

가정 1–4(결측 가정) 하에서 다음이 성립한다:

P(X, Y^*, Z \mid W, R_y=0) = P(X, Y, Z \mid W, R_y=0)

즉, $R_y$ 는 $(X, Y, Z)$ 와 $W$ 가 주어졌을 때 독립이다.
따라서 우리는 $R_y=0$ 인 데이터로부터
가상 데이터 샘플을 생성할 수 있다.

선형 가우시안(Linear Gaussian) 가정하에서

만약 데이터가 선형-가우시안 분포를 따른다면,
다음과 같은 선형 회귀모형을 적용할 수 있다:

X = \alpha_1 W + \varepsilon_1, \quad Y = \alpha_2 W + \varepsilon_2, \quad Z = \alpha_3 W + \varepsilon_3 \tag{2}

여기서:

$\alpha_i$ 는 각 회귀 모델의 파라미터,
$\varepsilon_i$ 는 잔차(residual)이다.

이렇게 학습된 모델을 이용하면
$P(W)$ 로부터 샘플링된 $W$ 값으로
결측되지 않은 $(X, Y, Z)$ 가상 데이터를 생성할 수 있다.

요약

단계	내용	결과
1️⃣	$P(X, Y, Z \mid W, R_y=0)$ 학습	결측 없는 부분으로 모델링
2️⃣	$P(W)$ 로부터 $W$ 재표본화	결측 원인 변수 분포 복원
3️⃣	$(X, Y, Z)$ 가상 데이터 생성	완전 데이터 근사
4️⃣	CI 검정 수행	불필요한 간선 제거

핵심 포인트

PermC는 결측 원인 변수 $W$ 를 사용하여
결측의 영향을 제거하고, “완전한 데이터의 구조”를 근사한다.
이렇게 생성된 가상 데이터로부터 인과 구조를 보다 정확히 복원할 수 있다.

Permutation-based Correction (PermC) — Implementation Details

앞서 PermC의 개념적 아이디어를 살펴보았다면,
이번에는 실제 적용 절차와 수식적 구현 방식을 다룬다.

가상 데이터 생성 (Virtual Data Generation)

결측이 없는 $W$ 의 완전한 데이터를 알고 있다면,
단순히 $P(W)$ 에서 샘플링하여 $P(X, Y, Z)$ 를 복원할 수 있다.
하지만 실제로는 $W$ 의 일부가 결측되었기 때문에
직접적으로 회귀 모델에 적용할 수 없다.

따라서 $W$ 를 무작위로 섞은(shuffled) 버전 $W^S$ 를 사용한다.

\hat{X} = \alpha_1 W^S + \varepsilon_1, \quad \hat{Y} = \alpha_2 W^S + \varepsilon_2, \quad \hat{Z} = \alpha_3 W^S + \varepsilon_3 \tag{3}

$W^S$ : 결측 없는 샘플의 값을 무작위로 재배열한(shuffled) 값
$\alpha_i$ : 각 회귀모델의 계수
$\varepsilon_i$ : 잔차 (residual)

즉, $W$ 의 구조를 유지하면서도 결측과의 상관을 끊어
결측 편향이 제거된 가상 데이터를 생성한다.

PermC 절차 요약

PermC가 올바르게 작동하는 조건 (Conditions for Validity of PermC)

PermC는 대부분의 결측 상황에서 효과적으로 작동하지만,
그 결과가 이론적으로 정확(consistent) 하려면 몇 가지 조건이 충족되어야 한다.
논문에서는 두 가지 핵심 조건 (i), (ii) 를 제시한다.

(i) 결측 지표의 직접 원인만 고려할 것

PermC는 결측의 원인 변수들이
직접적으로 결측 지표( $R$ )를 설명한다고 가정한다.

즉, 변수 $W$ 가 결측 지표들의 직접 원인(direct cause) 들을 모두 포함해야 한다:

\{R_x, R_y, R_z, R_w\} \perp\!\!\!\perp \{X, Y, Z\} \mid W

이를 간단히 표현하면 다음과 같다:

W = \text{Pa}(R_x, R_y, R_z, R_w)

$W$ : 결측 지표들의 부모 노드 (direct causes)
$\text{Pa}(R_i)$ : 결측 지표 $R_i$ 의 부모 집합

-> 즉, 결측의 발생이 $W$ 에 의해 완전히 설명될 수 있어야 한다는 뜻이다.

(ii) 결측 지표의 독립성 조건 유지

PermC가 가상 데이터에서 정확히 작동하려면,
결측 지표의 존재 여부가 변수 간의 독립성 구조를 왜곡하지 않아야 한다.

즉, 결측 여부( $R_w$ )를 추가로 고려해도
조건부 독립성의 관계가 변하지 않아야 한다:

X \perp\!\!\!\perp Y \mid Z \iff X \perp\!\!\!\perp Y \mid \{Z, R_w\}

이는 “결측 지표의 존재가 인과 구조에 영향을 주지 않는다”는 것을 의미한다.
다르게 말하면, $R_w$ 는 단순히 데이터의 누락을 나타내는 지표이지,
$X, Y, Z$ 의 인과관계에 새로운 종속성을 만들어서는 안 된다.

두 조건의 의미 요약

조건	수식	의미
(i)	$\{R_x, R_y, R_z, R_w\} \perp\!\!\!\perp \{X, Y, Z\} \mid W$	결측의 원인이 완전히 $W$ 로 설명됨
(ii)	$X \perp\!\!\!\perp Y \mid Z \iff X \perp\!\!\!\perp Y \mid \{Z, R_w\}$	결측 지표가 독립성 구조를 왜곡하지 않음

정리

이 두 조건이 모두 만족되면:

PermC는 관측된 데이터에서 진짜 인과 구조를 복원할 수 있다.
결측으로 인해 생긴 가짜 상관관계(spurious correlation) 를 제거할 수 있다.
결과적으로 TD-PC의 오류 간선을 성공적으로 교정한다.

수식적 연결

이 조건 하에서, 관측된 결측 없는 데이터 분포 $P(X, Y, Z \mid R_y=0)$ 와
결측이 없는 완전한 데이터 분포 $P(X, Y, Z)$ 의 관계는 다음처럼 표현된다:

P(X, Y, Z \mid R_y=0) = \int_W P(X, Y, Z \mid W, R_y=0) P(W \mid R_y=0) \, dW

이 식을 기반으로 PermC는 $W$ 를 재표본화하여
결측이 없는 가상 분포를 복원한다.

Density Ratio Weighted Correction (DRW)

PermC는 대부분의 MAR 상황에서 정확히 작동하지만,
조건 (i) 와 조건 (ii) 가 만족되지 않는 MNAR 상황에서는 여전히 오류 간선이 남을 수 있다.
이를 보완하기 위해 논문에서는 DRW (Density Ratio Weighted Correction) 기법을 제안한다.

아이디어

DRW는 결측 메커니즘이 더 복잡한 경우(즉, PermC 조건이 깨질 때)
데이터의 확률 밀도 비율(density ratio) 을 이용해
관측된 데이터의 분포를 보정(reweighting)하여 완전한 데이터 분포를 근사한다.

이를 통해 결측으로 인해 왜곡된 의존 구조를 복원하고,
불필요한 간선(extraneous edge)을 제거할 수 있다.

수식적 정의

DRW는 관심 변수 집합 $V_a$ 의 결합 확률분포 $P(V_a)$ 를
관측된 데이터로부터 다음과 같이 재구성한다.

P(V_a) = \frac{P(R = 0, V_a)}{\prod_i P(R_i = 0 \mid \text{Pa}(R_i), R_{\text{Pa}(R_i)} = 0)} = P(V_a \mid R = 0) \times c \times \prod_i \beta_{\text{Pa}(R_i)} \tag{5}

여기서

$R$ : 모든 결측 지표의 집합
$\text{Pa}(R_i)$ : 결측 지표 $R_i$ 의 부모 노드들
$\beta_{\text{Pa}(R_i)}$ : 각 결측 지표에 대한 밀도비
$c$ : 정규화 상수 (normalizing constant)

보정 상수 정의

정규화 상수 $c$ 와 밀도비 $\beta_{\text{Pa}(R_i)}$ 는 각각 다음과 같이 정의된다.

c = \frac{P(R = 0)}{\prod_i P(R_i = 0 \mid R_{\text{Pa}(R_i)} = 0)}

\beta_{\text{Pa}(R_i)} = \frac{P(\text{Pa}(R_i) \mid R_{\text{Pa}(R_i)} = 0)} {P(\text{Pa}(R_i) \mid R_i = 0, R_{\text{Pa}(R_i)} = 0)}

이 식들은 조건부 확률비율(conditional probability ratios) 을 이용하여
결측이 발생하지 않은 데이터( $R=0$ )를 가중 보정하는 과정이다.

구현 단계 요약

DRW의 절차는 다음과 같다.

1️⃣ 결측 제거 (Test-wise deletion)

$R = 0$ 인 레코드만 남긴 후 $P(V_a \mid R=0)$ 추정

2️⃣ 밀도비 계산 (Density Ratio Estimation)

각 결측 지표 $R_i$ 에 대해 $\beta_{\text{Pa}(R_i)}$ 계산
커널 밀도 추정(KDE; Sheather & Jones, 1991) 사용

3️⃣ 데이터 재가중 (Reweighting)

관측 데이터에 $\prod_i \beta_{\text{Pa}(R_i)}$ 와 $c$ 를 곱하여 가중치를 부여

4️⃣ CI 검정 수행 (Conditional Independence Testing)

재가중된 데이터로 조건부 독립성 검정 수행
결측으로 인한 오류 간선을 교정

DRW의 핵심 요약

항목	설명
핵심 목표	MNAR 상황에서 결측 편향 제거
핵심 아이디어	확률 밀도비를 이용한 데이터 재가중
적용 방법	$\prod_i \beta_{\text{Pa}(R_i)}$ 를 이용해 관측 데이터 보정
보정 효과	PermC가 다루지 못하는 복잡한 결측 구조 교정
한계	KDE 계산 비용이 높음 (추정 오차에 민감)

요약 정리

DRW는 PermC의 한계(MNAR 미처리) 를 보완하기 위해 제안된 기법이다.
결측 지표의 부모 노드 확률 분포를 추정하고,
각 샘플의 가중치를 밀도비로 조정(reweight) 하여
완전한 데이터의 분포를 근사한다.
결과적으로 PermC + DRW의 조합으로
MVPC는 MCAR, MAR, MNAR 모든 결측 메커니즘에 대응할 수 있다.

5. Experiments — 실험 결과

본 절에서는 제안된 MVPC (Missing Value PC) 알고리즘의 성능을
모의 데이터(synthetic data)와 실제 의료 데이터(real-world datasets)에서 평가한다.

MVPC는 다음 두 실제 연구 데이터에서도 테스트되었다.

CogUSA (Cognition and Aging Study) — 미국 인지·노화 관련 설문 데이터
(McArdle et al., 2015)
ATR (Achilles Tendon Rupture Study) — 아킬레스건 파열 재활 연구 데이터
(Praxitelous et al., 2017; Domeij-Arverud et al., 2016)

5.1 Synthetic Data Evaluation

모의 데이터 실험은 인과 구조가 사전에 알려진 상황에서
각 인과 탐색 알고리즘의 정확성을 비교하기 위해 수행되었다.

Baselines

비교 대상 알고리즘은 다음과 같다:

TD-PC : Test-wise Deletion PC
LD-PC : List-wise Deletion PC
Ideal PC : 완전한 데이터(결측 없음)에서의 PC 알고리즘
Target PC : 동일한 샘플 수를 가지는 MCAR 데이터에서의 기준선

MVPC의 목표는 Ideal PC와 유사한 결과를 내는 것이다.

Data Generation

모의 데이터 생성 과정은 다음과 같다:

1️⃣ 무작위 Gaussian DAG (Directed Acyclic Graph) 생성
2️⃣ DAG 기반으로 데이터 샘플링
3️⃣ 최소 2개 이상의 collider 구조(→ 인과 혼선 구조) 포함
4️⃣ 결측 메커니즘 반영:

MAR (Missing At Random)
MNAR (Missing Not At Random)

각 데이터셋은 변수 20개 또는 50개로 구성되며,
결측 비율이 부분적으로 다르게 설정되었다.
샘플 크기는 100, 1000, 5000, 10000으로 설정하였다.
→ 총 400개의 DAG 생성.

5.1.1 Results on Synthetic Data

결과는 두 가지 주요 지표로 평가되었다:

Structural Hamming Distance (SHD)
→ 실제 인과 구조와의 간선 차이 (작을수록 좋음)
Adjacency & Orientation Precision / Recall
→ 간선의 존재 여부와 방향성 정확도 (높을수록 좋음)

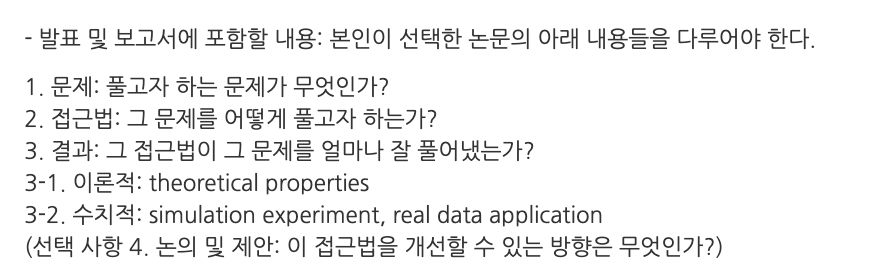
조건	특징	결과 요약
(a) MAR (20 variables)	결측이 무작위로 발생	MVPC가 TD-PC 및 LD-PC보다 낮은 SHD
(b) MNAR (20 variables)	일부 변수에 비무작위 결측	MVPC는 target에 근접, LD-PC는 큰 오차
(c) MNAR (50 variables)	더 많은 변수 + 결측 다양성	MVPC는 안정적, LD-PC는 급격히 성능 저하

→ 결론: MVPC는 데이터 크기가 증가할수록 안정적이며,
결측 구조가 복잡해도 “Target PC”에 가장 근접한 결과를 보임.

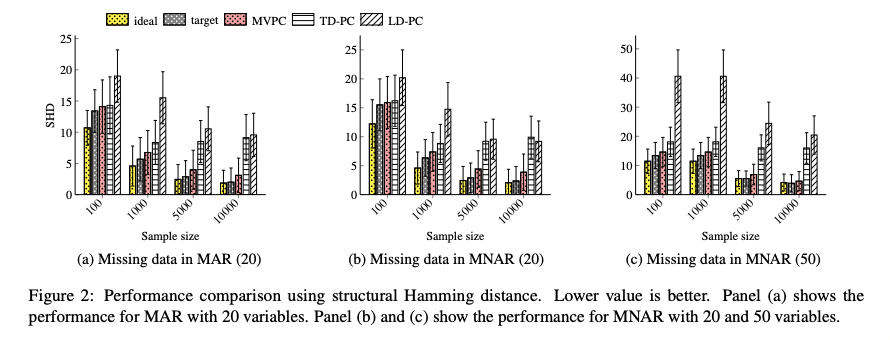
조건	Metric	결과 요약
(a) MAR	Adjacency	MVPC의 정확도, 재현율 모두 가장 높음
(b) MAR	Orientation	MVPC가 방향성 복원에서도 안정적
(c) MNAR	Adjacency	결측이 심한 경우에도 일관된 성능 유지
(d) MNAR	Orientation	TD-PC보다 높은 방향성 일치율

→ 결론: MVPC는

결측 비율이 높은 데이터(MNAR)에서도 강건함,
기존 deletion 기반 방법보다 방향성 복원 성능이 우수함.

💬 전체 요약

비교 기준	TD-PC	LD-PC	MVPC
SHD (낮을수록 좋음)	△	✕	✅
Precision / Recall	△	✕	✅
Large sample 효율성	✅	✕	✅
MNAR 대응력	✕	✕	✅

📈 결론:
MVPC는 기존 방법 대비 SHD 최소화, 정확도 향상, 결측 유형(MCAR/MAR/MNAR) 전반 대응력에서
모두 우수한 성능을 보인다.

5.2 The Cognition and Aging Study (CogUSA)

CogUSA 데이터셋은 대규모 인지·노화 관련 설문조사 기반으로,
결측이 상당히 많은 실세계 데이터(real-world data)이다.
이 연구에서는 MVPC를 사용하여
인지 능력, 건강, 사회적 요인 간의 인과 관계를 분석하였다.

데이터 유형: 설문 기반 심리·행동 데이터
결측 메커니즘: MCAR, MAR, MNAR 혼재
분석 목표: 인과 그래프 복원 및 불필요한 간선 제거

5.3 Achilles Tendon Rupture Study (ATR Study)

이번에는 실제 의료 데이터인 Achilles Tendon Rupture (ATR) 재활 연구 데이터를 통해
MVPC의 성능을 검증하였다.
해당 데이터는 여러 병원에서 수집된 환자 재활 관련 데이터이며
약 70% 이상이 결측된(highly missing) 상태이다
(Praxitelous et al., 2017; Hamesse et al., 2018).

데이터 특성

데이터 유형:
근골격계 재활 및 회복 관련 임상 데이터
결측 비율:
약 70% (완전한 환자 데이터가 거의 없음)
분석 변수:
100개 이상의 임상 변수 포함

결측이 매우 심각하여 기존의 list-wise deletion 방식은 적용이 불가능했기 때문에,
MVPC와 TD-PC를 각각 적용하여 비교하였다.

분석 결과

아래는 실험에서 사용된 주요 변수들이다:

변수	설명
Age	환자 나이
Gender	성별
BMI	체질량 지수 (Body Mass Index)
LSI	Limb Symmetry Index — 좌우 다리 근력 비율
FAOS	Foot and Ankle Outcome Score — 발목 회복 점수
Oₚₜᵢₘₑ	수술 시점(Operation Time)
S	FAOS 결측을 유발하는 보조 변수 (auxiliary variable)

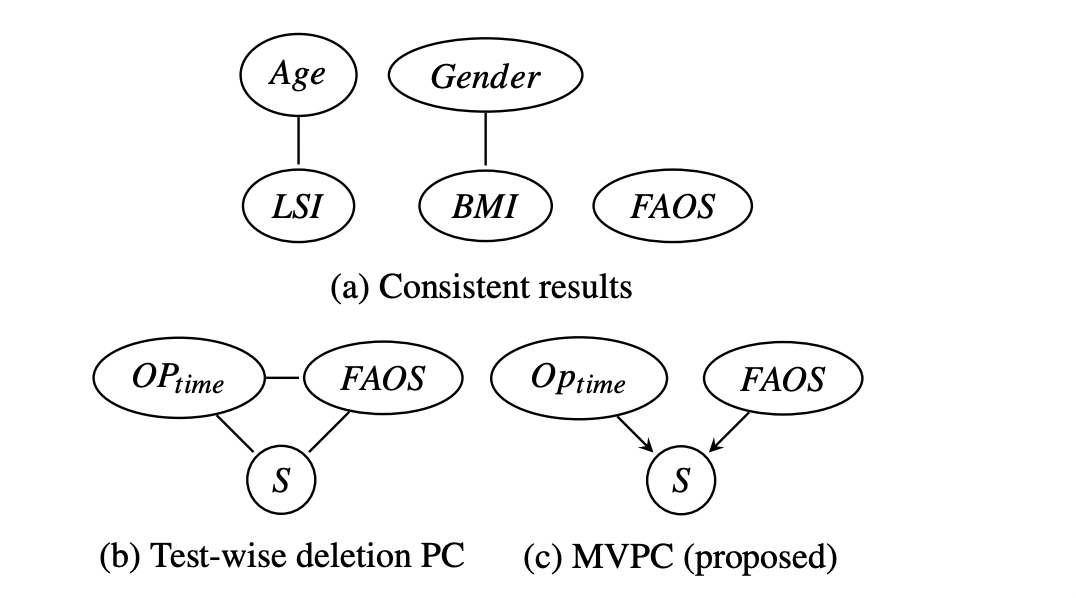
(a) 는 MVPC로 도출된 인과 그래프 일부를 보여준다.

Age, Gender, BMI, LSI → FAOS 간 인과 관계는
의학적 상식과 일치하며, 모델의 신뢰성을 뒷받침한다.

(b) 는 TD-PC 결과로,
Operation Time → FAOS 간 불필요한 간선(extraneous edge) 이 존재한다.

(c) 는 MVPC 결과로,
해당 오류 간선을 성공적으로 제거하였다.

즉, MVPC는 결측으로 인한 잘못된 상관 구조를 교정하고
의학적으로 일관된 인과 구조를 복원한다.

CogUSA 결과 요약 (비교)

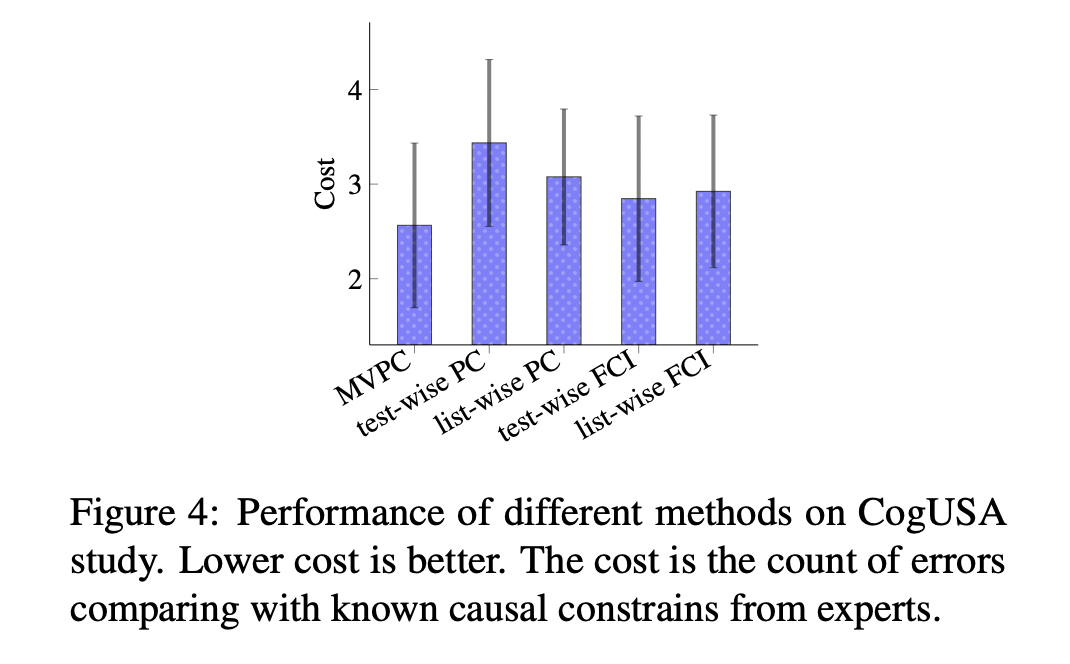
알고리즘	오류 개수(Cost) ↓	특징
MVPC	최저 (Best)	전문가 인과 제약 조건과 가장 일치
Test-wise PC	중간	일부 결측 영향 존재
FCI / Deletion-based	높음	결측으로 인한 오류 다수

📈 결론: CogUSA와 ATR 모두에서 MVPC가 가장 낮은 오류율과 안정된 인과 복원 성능을 보였다.

6. Discussion (논의)

이번 연구는 결측 데이터가 존재하는 상황에서의
인과 발견(Causal Discovery) 문제를 다루었다.

주요 내용 요약

1️⃣ 이론적 분석 (Theoretical Analysis)

결측 메커니즘(MCAR, MAR, MNAR)에 따른
오류 간선의 발생 조건을 수학적으로 규명함.

2️⃣ 새로운 알고리즘 제안 (MVPC)

PermC와 DRW를 결합한 새로운 인과 탐색 알고리즘 제안.
경미한 가정(assumptions) 하에서
비대칭 결측 데이터에서도 정확한 인과 구조 복원 가능.

3️⃣ 실험적 검증 (Experiments)

모의 데이터와 두 실제 의료 데이터셋(CogUSA, ATR)을 통해
MVPC의 효용성과 정확성을 검증함.
SHD, Precision/Recall 등 모든 지표에서 기존 방법 대비 우수한 성능을 달성.

연구 의의

기존의 PC 기반 인과탐색은 결측이 있는 데이터에서 잘못된 결론을 내릴 수 있었으나,
MVPC는 결측을 직접 보정하면서 올바른 인과 구조를 복원할 수 있다.
실험을 통해,
MCAR, MAR, MNAR 모든 결측 메커니즘에서 안정적으로 작동함을 확인하였다.
향후에는 대규모 의료 데이터에서의 확장 적용 가능성이 크다.

향후 연구 방향 (Future Work)

MVPC의 가정을 완화(relaxation)하여
더 다양한 결측 구조에도 적용 가능하도록 개선 예정.
대규모 의료 및 사회과학 데이터셋에서
협업 기반 인과 분석 (collaborative causal analysis) 으로 확장할 계획.

구조적 해밍 거리(SHD): 네트워크 구조 간의 차이를 정량화하는 척도입니다. 즉, 하나의 그래프 구조를 다른 그래프 구조로 변환하기 위해 필요한 최소한의 편집(edge additions, deletions, reversals) 작업 횟수

yeorurirurariru

이전 포스트

[Paper Review]A Self-Supervised Mixture-of-Experts Framework for Multi-behavior Recommendation

다음 포스트