다익스트라/데이크스트라 알고리즘

a·2023년 8월 11일

알고리즘

목록 보기

8/17

다익스트라/데이크스트라 알고리즘

다익스트라 알고리즘은 DP활용한 최단경로 탐색 알고리즘입니다. 특정한 하나의 노드에서 특정한 노드로 가는 최단경로를 알려줍니다. 이 때 음의 간선을 포함할 수 없습니다. gps와 같이 실제로 사용하기 적합한 알고리즘입니다.

인접 행렬로 구현하는 경우

시간 복잡도 : O(V^2)
공간 복잡도 : O(V^2)

인접 리스트와 힙(=우선순위 큐)을 사용하는 경우

시간 복잡도 : O(ElogV)
우선순위 큐에서 꺼낸 현재 노드에 연결된 간선 모두 확인 - 간선의 개수(E) 만큼 확인
우선순위 큐에 간선을 넣고 빼는 과정 - logE
모든 간선을 우선순위 큐에 넣고 뺀다고 했을 때 O(ElogE) 의 시간 복잡도=
이때, 중복 간선을 포함하지 않는 경우, E는 항상 V^2 이하이다. (모든 노드가 연결 되어 있는 경우 V * (V-1))
logE < log(V^2)이다. log(V^2)은 2logV이기 때문에 O(logV)로 표현할 수 있다.
따라서, 다익스트라 알고리즘 전체 시간 복잡도를 O(ElogV) 로 표현할 수 있다. (ElogE)

다익스트라 알고리즘이 DP인 이유
최단 거리는 여러 개의 최단 거리로 이루어져, 하나의 최단 거리를 구할 때 이전까지 구했던 최단 거리 정보를 활용하여 사용합니다.

동작 단계

① 출발 노드와 도착 노드를 설정합니다.
② '최단 거리 테이블'을 초기화합니다.
③ 현재 위치한 노드의 인접 노드 중 방문하지 않은 노드를 구별하고, 방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택합니다. 그 노드를 방문 처리합니다.
④ 해당 노드를 거쳐 다른 노드로 넘어가는 간선 비용(가중치)을 계산해 '최단 거리 테이블'을 업데이트합니다.
⑤ ③~④의 과정을 반복합니다.

'최단 거리 테이블'은 1차원 배열로, N개 노드까지 오는 데 필요한 최단 거리를 기록합니다. N개(1부터 시작하는 노드 번호와 일치시키려면 N + 1개) 크기의 배열을 선언하고 큰 값을 넣어 초기화시킵니다.

'노드 방문 여부 체크 배열'은 방문한 노드인지 아닌지 기록하기 위한 배열로, 크기는 '최단 거리 테이블'과 같습니다. 기본적으로는 False로 초기화하여 방문하지 않았음을 명시합니다.

동작 예

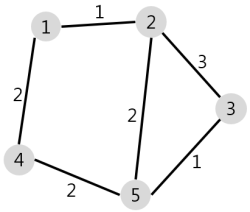
우선 위의 graph를 이차 배열로 나타냅니다.

∞	1	∞	2	∞
1	∞	3	∞	2
∞	3	∞	∞	1
2	∞	∞	∞	2
∞	2	1	2	∞

출발 노드를 먼저 선택하고 거리를 0으로 한 뒤, 거리 테이블을 전부 큰 값, 여기서는 ∞로 초기화합니다.

방문	X	X	X	X	X
노드	1	2	3	4	5
거리	0	∞	∞	∞	∞

1번 노드와 거리 테이블을 비교하여

0	∞	∞	∞	∞
∞	1	∞	2	∞

작은 값으로 거리를 변경하고 방문 표시를 합니다.

방문	O	X	X	X	X
노드	1	2	3	4	5
거리	0	1	∞	2	∞

방문하지 않는 노드 중 가장 거리값이 작은 번호인 2번 노드를 다음 노드로 택합니다.
이 때 2번 노드는 2번 노드까지 걸린 최단 거리를 더해 줍니다.

0	1	∞	2	∞
1 + 1	∞	3 + 1	∞	2 + 1

작은 값으로 거리를 변경하고 방문 표시를 합니다.

방문	O	O	X	X	X
노드	1	2	3	4	5
거리	0	1	4	2	3

4번 노드로 이동 후 위의 과정을 반복합니다.

0	1	4	2	3
2 + 2	∞	∞	∞	2 + 2

작은 값으로 거리를 변경하고 방문 표시를 합니다.

방문	O	O	X	O	X
노드	1	2	3	4	5
거리	0	1	4	2	3

5번 노드로 이동 후 위의 과정을 반복합니다.

0	1	4	2	3
∞	2 + 3	1 + 3	2 + 3	∞

작은 값으로 거리를 변경하고 방문 표시를 합니다.

방문	O	O	X	O	O
노드	1	2	3	4	5
거리	0	1	4	2	3

3번 노드로 이동 후 위의 과정을 반복합니다.

0	1	4	2	3
∞	3 + 4	∞	∞	1 + 4

작은 값으로 거리를 변경하고 방문 표시를 합니다.

방문	O	O	O	O	O
노드	1	2	3	4	5
거리	0	1	4	2	3

최종적으로 1번 노드에서 각 노드까지의 최단 거리는 1, 4, 2, 3입니다.

구현 방법

다익스트라 알고리즘을 구현하는 방법에는 '방문하지 않은 노드'를 다루는 방식에서 '순차 탐색'을 할 것이나 '우선순위 큐'를 쓸 것이냐로 나뉩니다.
https://school.programmers.co.kr/learn/courses/30/lessons/132266
위 문제 풀이 방식입니다.

순차 탐색

'방문하지 않은 노드 중 거리값이 가장 작은 노드'를 선택해 다음 탐색 노드로 삼습니다. 그 노드를 찾는 방식이 순차 탐색이 됩니다. 즉 거리 테이블의 앞에서부터 찾아내야 하므로 노드의 개수만큼 순차 탐색을 수행해야 합니다. 따라서 노드 개수가 N이라고 할 때 각 노드마다 최소 거리값을 갖는 노드를 선택해야 하는 순차 탐색이 수행되므로 (N−1)×N=O(N^2)의 시간이 걸립니다.

import java.util.Arrays;

class Solution {
    public int[] solution(int n, int[][] roads, int[] sources, int destination) {
        int[] answer = new int[sources.length];
        int[][] graph = new int[n][n];

        for (int i = 0; i < graph.length; i++) {
            Arrays.fill(graph[i], Integer.MAX_VALUE);
        }

        for (int i = 0; i < roads.length; i++) {
            graph[roads[i][0] - 1][roads[i][1] - 1] = 1;
            graph[roads[i][1] - 1][roads[i][0] - 1] = 1;
        }

        for (int i = 0; i < sources.length; i++) {
            answer[i] = dijkstra(n, graph, sources[i], destination);
        }

        return answer;
    }

    private int dijkstra(int n, int[][] graph, int source, int destination) {
        int[] distance = new int[n];
        Arrays.fill(distance, Integer.MAX_VALUE);
        distance[destination - 1] = 0;

        boolean[] visited = new boolean[n];

        for (int i = 0; i < n - 1; i++) {
            int minDistance = Integer.MAX_VALUE;
            int minIndex = -1;

            for (int j = 0; j < n; j++) {
                if (!visited[j] && distance[j] < minDistance) {
                    minDistance = distance[j];
                    minIndex = j;
                }
            }

            if (minIndex == -1) {
                break;
            }

            visited[minIndex] = true;

            for (int j = 0; j < n; j++) {
                if (!visited[j] && graph[minIndex][j] != Integer.MAX_VALUE && distance[minIndex] + graph[minIndex][j] < distance[j]) {
                    distance[j] = distance[minIndex] + graph[minIndex][j];
                }
            }
        }

        return distance[source - 1] == Integer.MAX_VALUE ? -1 : distance[source - 1];
    }
}

Integer.MAX_VALUE를 사용할 경우 int의 범위에서 벗어나 오버플로우로 음수로 변환될 수 있습니다.

우선순위 큐

우선순위 큐에서 사용할 '우선순위'의 기준은 '시작 노드로부터 가장 가까운 노드'가 됩니다. 따라서 큐의 정렬은 최단 거리인 노드를 기준으로 최단 거리를 가지는 노드를 앞에 배치합니다.

위의 순차 탐색을 쓰는 구현과는 다르게 우선순위 큐를 사용하면 방문 여부를 기록할 배열은 없어도 됩니다. 우선순위 큐가 알아서 최단 거리의 노드를 앞으로 정렬합니다. 만약 기존 최단거리보다 더 작은 값을 가지는 노드가 있다면 그 노드와 거리를 우선순위 큐에 넣습니다.

import java.util.*;

class Solution {
    public int[] solution(int n, int[][] roads, int[] sources, int destination) {
        int[] answer = new int[sources.length];
        List<List<Node>> graph = new ArrayList<>();

        // 그래프 초기화
        for (int i = 0; i <= n; i++) {
            graph.add(new ArrayList<>());
        }

        // 도로 정보로 그래프 구성 (양방향)
        for (int[] road : roads) {
            int u = road[0] - 1;
            int v = road[1] - 1;
            graph.get(u).add(new Node(v, 1));
            graph.get(v).add(new Node(u, 1));
        }

        // 다익스트라 알고리즘을 위한 배열 초기화
        int[] time = new int[n];
        Arrays.fill(time, Integer.MAX_VALUE);
        time[destination - 1] = 0;

        // 우선순위 큐를 사용한 다익스트라 알고리즘
        PriorityQueue<int[]> pq =
    new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));

        // PriorityQueue<Node> pq = new PriorityQueue<>((o1, o2) -> o1.cost - o2.cost);
        // 문자일 경우
        // PriorityQueue<Node> pq = new PriorityQueue<>((o1, o2) -> o1.cost.compareTo(o2.cost));
        pq.offer(new Node(destination - 1, 0));

        while (!pq.isEmpty()) {
            Node curr = pq.poll();

            if (curr.time > time[curr.node]) {
                continue;
            }

            for (Node neighbor : graph.get(curr.node)) {
                int newTime = curr.time + neighbor.time;
                if (newTime < time[neighbor.node]) {
                    time[neighbor.node] = newTime;
                    pq.offer(new Node(neighbor.node, newTime));
                }
            }
        }

        // 각 출발지에 대한 결과 계산
        for (int i = 0; i < sources.length; i++) {
            int source = sources[i] - 1;
            answer[i] = time[source] == Integer.MAX_VALUE ? -1 : time[source];
        }

        return answer;
    }
    
    // 그래프에서 사용할 Node 클래스
    class Node {
        int node;
        int time;

        public Node(int node, int time) {
            this.node = node;
            this.time = time;
        }
    }
}

노드가 탐색되지 않았다는 것을 나타내는 무한대 값은 graph가 비어있는 상태로 알 수 있기 때문에, 초기 값을 무한대로 설정하지 않아도 됩니다.

참고

https://velog.io/@717lumos/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%8B%A4%EC%9D%B5%EC%8A%A4%ED%8A%B8%EB%9D%BCDijkstra-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

이전 포스트

DP, 다이나믹 프로그래밍(동적 계획법) 피보나치 수

다음 포스트

순열

1개의 댓글

happy

2023년 8월 11일

이런 유용한 정보를 나눠주셔서 감사합니다.

답글 달기