휴가 낸거 복습하기..
1. 가설 검정
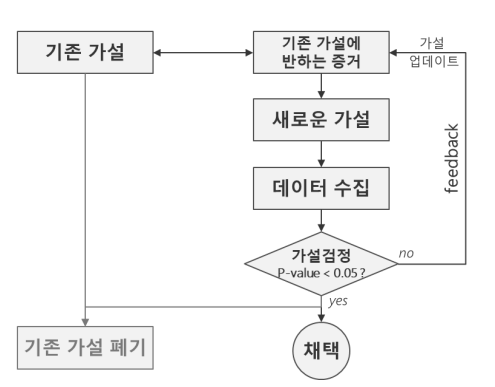
과학 연구 절차
모집단(Population)과 표본(Sample)
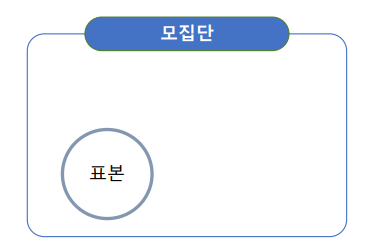
모집단 : 우리가 알고 싶은 대상 전체 영역 (데이터)
표본 : 그 대상의 일부 영역 (데이터)
우리는 일부분으로 전체를 추정하고자 한다!
- 모집단에 대한 가설 수립
- 가설은 보통 x와 y 관계를 표현
- X에 따라 Y가 차이가 있다.
- X와 Y는 관계가 있다.
- 표본을 가지고 가설이 진짜 그러한 지 검증!
귀무 가설 : 당신의 주장

- 영가설
- 현재의 가설
- 보수적인 입장
대립가설 : 나의 주장
- 연구가설
- 새로운 가설
- 내가 바라는 바
통계적 검정
-
표본으로부터 대립가설을 확인 -> 모집단에서도 맞을 것이라 주장
-
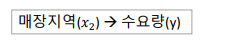
대립가설 : 매장지역(𝑥2)에 따라 수요량(𝑦)에 차이가 있다.
-
귀무가설 : 매장지역(𝑥2)에 따라 수요량(𝑦)에 차이가 없다.
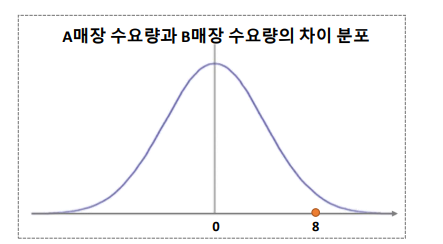
-
-
표본 평균 -> 정규 분포를 따른다.
-
표본1 평균 - 표본2 평균 -> 정규 분포를 따른다
분포 + 판단 기준 필요
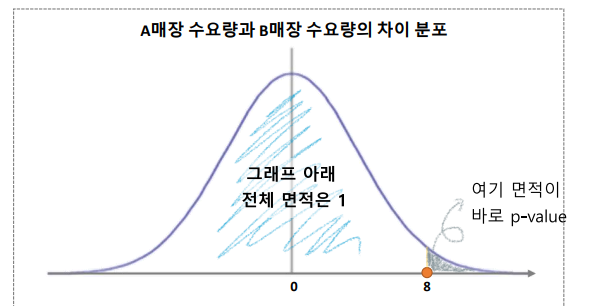
-
판단 기준 : p-value가 0.05 혹은 보수적인 기준으로 0.01를 사용
-
0.05 보다는 p-value가 작아야, 차이가 있다고 판단.
검정 통계량
: 검정(차이가 있는지 없는지 확인) 하기 위한 차이 값
-
t 통계량
-
x^2(카이제곱) 통계량
-
f 통계량
이를 손쉽게 판단할 수 있도록 계산해 준 것이 p-value
2. 이변량 분석 : 숫자->숫자
도구
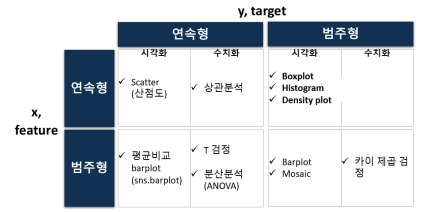
숫자 vs 숫자 - 정리하는 두가지 방법
1. 산점도 (Scatter)
- 그대로 점을 찍어서 그래프를 그려봄
2. 공분산(covariance), 상관 계수 (correlation efficient)
- 각 점들이 얼마나 직선에 모여있는지를 계산
시각화 : 산점도
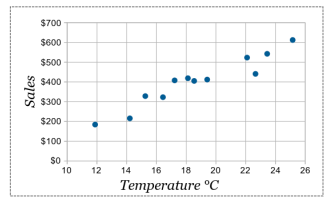
- 산점도 : 두 숫자형 변수의 관계를 나타내는 그래프
- 직선(Linearity) : 숫자 vs 숫자를 비교할 때 중요한 관점
문법
- Matplotlib
- plt.scatter(x=,y=)
- plt.scatter('x변수','y변수',data=df)
#라이브러리 불러오기
import matplotlib.pyplot as plt
#plt.scatter(air['Temp'], air['Ozone'])
plt.scatter('Temp', 'Ozone', data = air)
plt.show()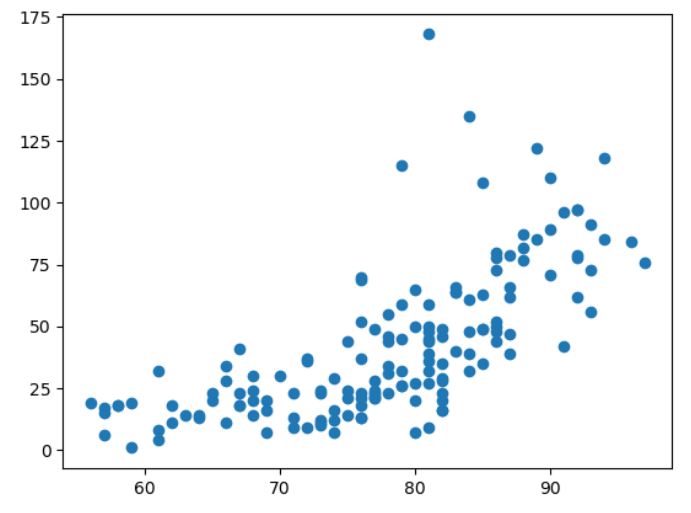
- seaborn
- sns.scatterplot('x변수','y변수'data=df)
# 라이브러리
import seaborn as sns
sns.scatterplot(x='Temp', y='Ozone', data = air)
plt.show()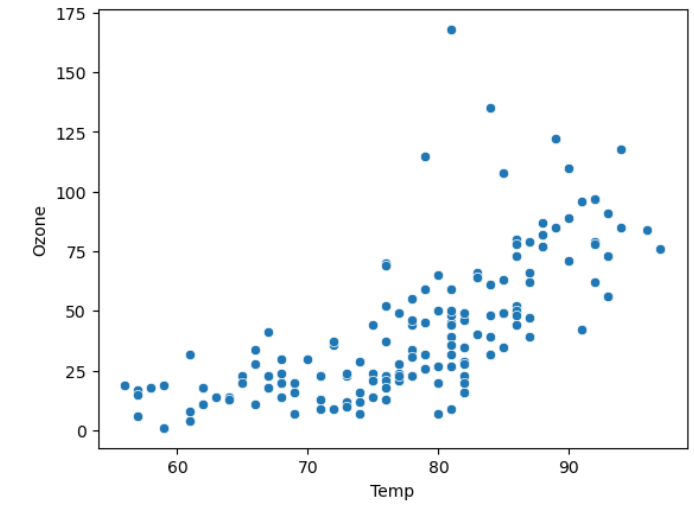
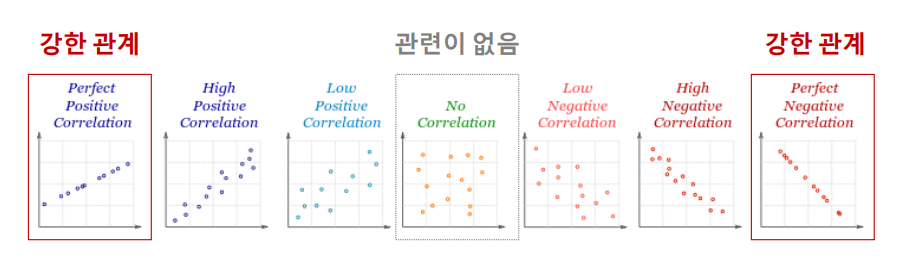
산점도에서의 관계 ?
- 얼마나 직선에 모여 있는가 -> 강한 관계
- x와 y의 관계를 얼마나 직선으로 잘 설명할 수 있는가
시각화 : 한번에 산점도 그리기
- sns.pairplot(dataframe)
- 숫자형 변수들에 대한 산점도를 한꺼번에 그려줌
- 시간 많이 걸림
- 일일이 확인하기 어려움
수치화 : 상관계수, 상관분석
눈으로 그래프를 살펴보며 관계를 파악하는 것은 어려움
-> 관계를 숫자로 계산해서 비교!
상관계수(r) : 관계를 수치화
- -1~1 사이의 값
- 상관계수끼리 비교 가능
- -1,1에 가까울 수록 강한 상관관계
- 0에 가까울수록 약한 상관관계

상관분석 : 상관계수가 유의미한지를 검정(test)
- scipy.stats 모듈 (통계 모듈)
spst.pearsonr(df['x'],df['y'])- 주의 : NaN(.notnull())을 빼고 계산
- 결과 : (상관계수, p-value) 의 튜플 형태
# 라이브러리 import scipy.stats as spst # 상관계수와 p-value spst.pearsonr(air['Temp'], air['Ozone'])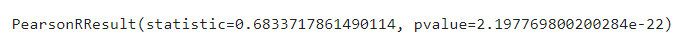
p-value
- 관계를 수치화한 값이 유의미한지 판단하는 숫자
- 판단 기준 (유의수준) -> 대립가설과 귀무가설에 따라 의미는 달라짐
- p-value < 0.05 : 두 변수 간에 관계가 있다. (상관관계가 있다고 판단)
- p-value >= 0.05 : 두 변수 간에 관계가 없다.
- df으로부터 한꺼번에 상관계수 구하기
- 모든 숫자형 변수들간 상관계수 계산
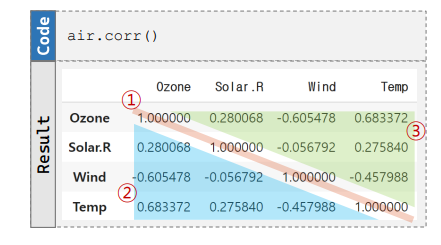
- df.corr()
- 대각선은 무시
- 1혹은 -1에 가까울수록 강한 관계