3. 평균 추정과 신뢰구간
평균과 분산, 표준편차
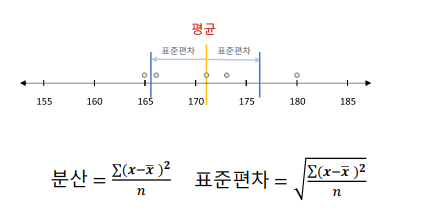
분산(Var, Variance)
- 데이터가 평균으로부터 얼마나 흩어져 있는지를 나타내는 통계적 척도
표준편차(SD, Standard Deviation)
- 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는 통계적 척도
- 분산의 제곱근
- 이탈도 (devlation)
- 데이터의 변동성
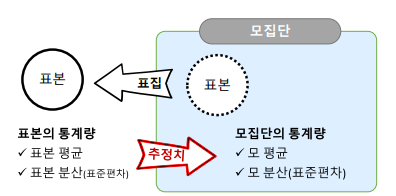
모집단과 표본
Sampling (표집)
- 전체 모집단에서 일부를 선택하여 데이터를 수집하는 과정 (모집단 추정)
표본 평균
- 모 평균에 대한 추정치
- 표준 오차 : 추정치의 오차 (표본 평균의 표준 편차)
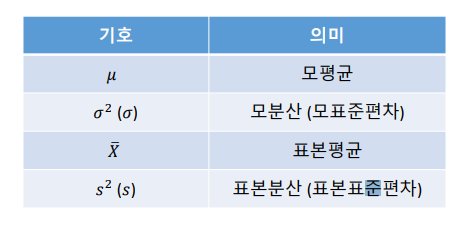
기호
조사 방법
- 표본 조사 : 모집단을 대표할 수 있는 일부 표본을 선택하여 데이터를 수집하는 방법
- 추출 방식 : 많은수 , 무작위
- 장점 : 적절한 비용과 시간
- 오차가 존대
- 전수 조사 : 전체(모집단을 조사)
- 장점 : 정확
- 비용, 시간 과다
중심 극한 정리 (Central Limit Theorem)
- 충분히 큰 크기의 표본을 뽑을 때, 이 표본의 평균은 모집단의 평균을 중심으로 하는 정규 분포를 따른다는 이론
- 표본의 크기가 클수록 정규 분포 모양이 중심에 가까워지는 좁은 형태가 됨 !
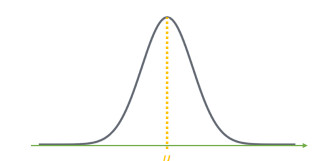
- ex) 전국 고등학생 50명을 무작위로 뽑아 평균을 계산 , 100번 반복 ➔ 각각의 평균 값 100개를 얻음
- 평균들의 분포( 표집 분포) -> 정규 분포에 가까워짐
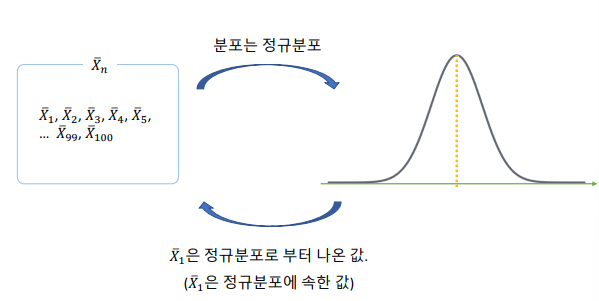
표준 오차 (Standard Error,SE)
-
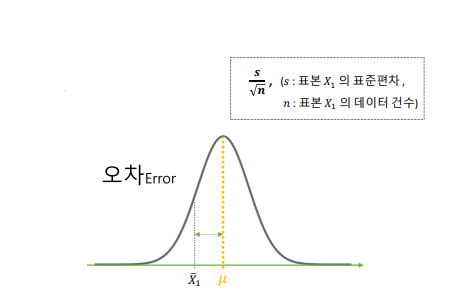
추정치의 오차 (표본 평균의 표준 편차)
-
모평균 𝜇 : 추정하고 싶은 정답
-
표본 평균 : 모평균에 대한 추정치 (예측치)
-
모평균과 표본 평균의 차이 : 오차error
-
표본 평균들 분포의 표준편차 : 표준 오차
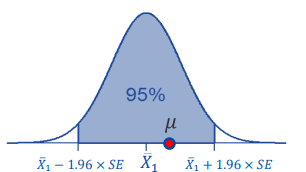
95% 신뢰구간 (Confidence Interval)
표준 오차(SE)를 바탕으로 95% 확률 구간을 구할 수 있다.
- 95% 신뢰 구간의 의미
- 쉬운 의미 : 신뢰구간 안에 모평균이 포함될 확률이 95%
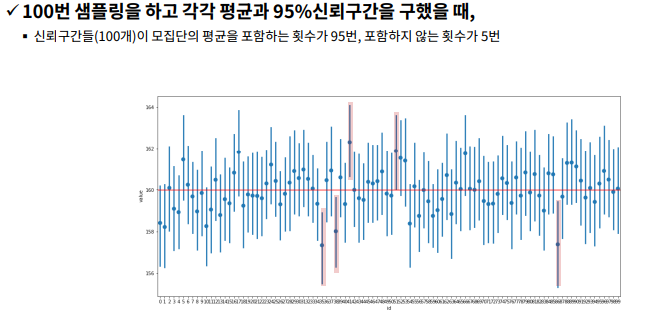
- 정확한 설명 : 표본을 100번 정도 뽑으면 95번 정도는 95% 신뢰구간 안에 모평균을 포함함.
4. 이변량 분석 : 범주 -> 숫자
범주 vs 숫자 - 비교하는 방법
평균 비교 barplot
- 범주가 2개 : 두 평균의 차이 비교
- 범주가 3개 이상 : 전체 평균과 각 범주의 평균 비교
시각화 : 두 집단(범주) -> 숫자
예시 대립가설: 생존여부에따라나이의차이가있다.
- 평균 비교 barplot
- 신뢰 구간(오차 범위)
- 좁을 수록 믿을 만 하다
- 데이터가 많을수록, 편차가 적을 수록 신뢰구간은 좁아짐
- 두 평균의 차이가 크고, 신뢰구간은 겹치치 않을 때, 대립 가설이 맞다고 볼 수 있다.
sns.barplot(x="Survived", y="Age", data=titanic)
plt.grid()
plt.show()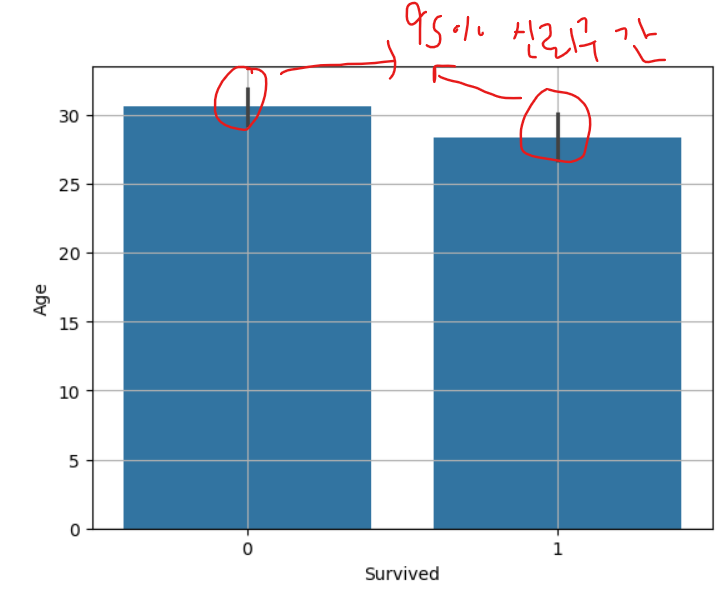
수치화 : t-test, anova (분산 분석)
두 집단(범주)의 평균 비교 :T-test
-
t 통계량 : 두 그룹의 평균 차이를 표준 오차로 나눈 값. ( 두평균의 차이로 이해해도 됨)
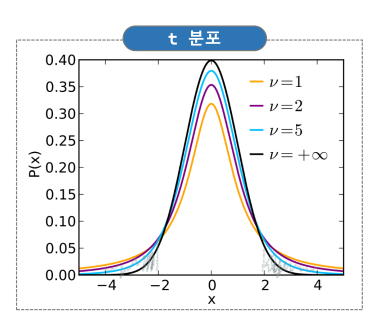
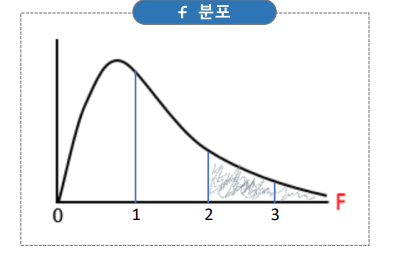
- t 통계량의 분포
-
t 통계량이 유의한지 검정
- T-test : t 통계량, p-value
- p-valuse가 0.05보다 작으면 관계가 있다.
- t 통계량이 -2보다 작거나, 2보다 크면 관계가 있다고 봄.
- p-valuse가 0.05보다 작으면 관계가 있다.
- T-test : t 통계량, p-value
-
ttest_ind(B,A,equal_var=False)
- NaN 행 제외 필수
- A와 비교할 때 B의 평균이 큰가?
- eual_var : A와 B의 분산이 같은가? 모르면 False(defualt)
# NaN 행 제외
temp = titanic.loc[titanic['Age'].notnull()]
# 두 그룹으로 데이터 저장
died = temp.loc[temp['Survived']==0, 'Age']
survived = temp.loc[temp['Survived']==1, 'Age']
#t-test
spst.ttest_ind(died, survived)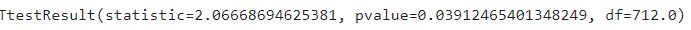
-
해석
- t-통계량 : 2.067 ➔ 2보다 크므로, 차이가 있기는 있으나 크지는 않다
- P-value : 0.039 ➔ 0.05 보다 작으므로, 차이가 있기는 있으나 크지는 않다
셋 이상 집단(범주)의 숫자 비교 - ANOVA
분산 분석 ANalysis Of VAriance
-
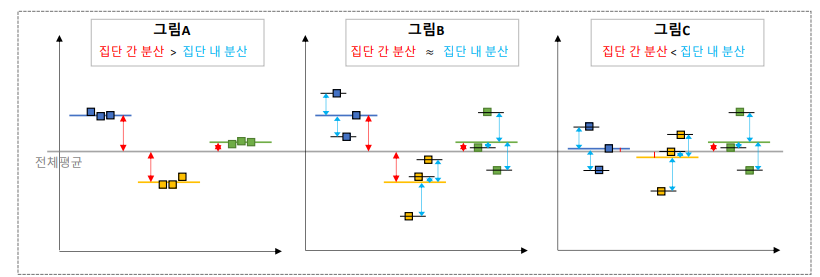
여러 집단 간에 차이 비교 : 기준은 전체 평균
-
F 통계량 = 집단 간 분산 / 집단 내 분산 = (전체평균 - 각 집단 평균)/(각 집단의 평균 - 개별 값)
- f-통계량 값이 대략 2~3 이상이면 관계가 있다고 판단
- p-value가 0.05보다 작으면 관계가 있다고 판단
- F통계량이 클 수록 가설이 맞다. (집단 내 분산이 작을수록, 집단 간 분산이 클수록)
f_oneway(A,B,C)
- 전체 평균과 A, B, C 각각의 평균은 차이가 있는가?
# 1) 분산 분석을 위한 데이터 만들기
# NaN 행 제외
temp = titanic.loc[titanic['Age'].notnull()]
# 그룹별 저장
P_1 = temp.loc[temp.Pclass == 1, 'Age']
P_2 = temp.loc[temp.Pclass == 2, 'Age']
P_3 = temp.loc[temp.Pclass == 3, 'Age']
spst.f_oneway(P_1, P_2, P_3)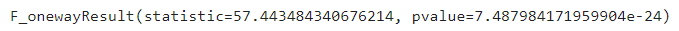 
- 관련이 크다
5. 이변량 분석 : 범주 -> 범주
분석 방법 : 교차표(crosstab)
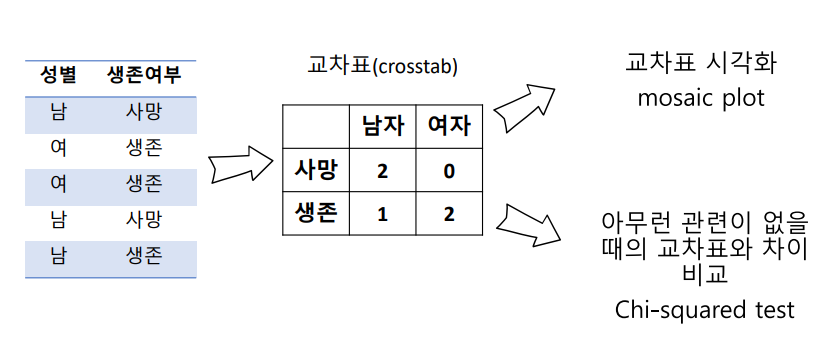
pd.crosstab(행,열)
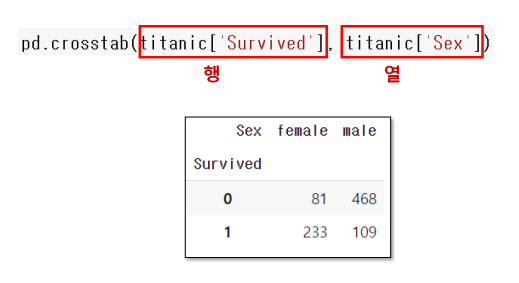
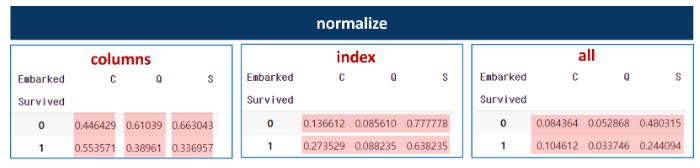
pd.crosstab(행,열, normalize=)
- normalize 옵션 : 비율로 변환
- columns : 열 기준 100%
- index : 행 기준 100%
- all : 전체 기준 100%
범주 -> 범주 시각화 : mosaic plot(data,['x','y'])
- 범주별 양과 비율을 나타냄
- 빨간 선은 전체 평균
mosaic(titanic, [ 'Pclass','Survived'])
plt.axhline(1- titanic['Survived'].mean(),
color = 'r')
plt.show()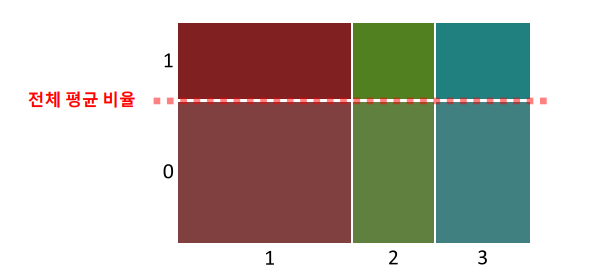
참고 : 그래프 사이즈 (세션 전체 적용)
plt.rcParams["figure.figsize"]=(8, 6)
해석
- X축 길이는 각 객실등급별 승객비율을 나타냄
- 그 중 3등급 객실에 대해서 보면, y축의 길이는, 3등급 객실 승객 중에서 사망, 생존 비율을 의미
두 범주형 변수가 아무런 상관이 없다면 ?
- 범주 별 비율의 차이가 전혀 없음
- 조금이라도 관련이 있다면, 비율 혹은 bar의 크기에 조금이라도 차이가 남
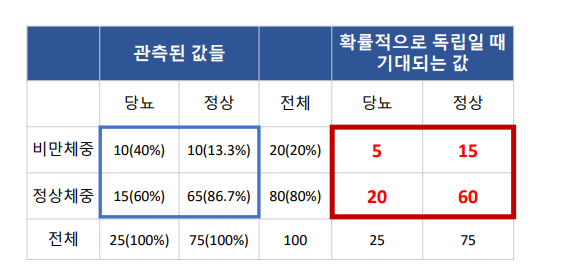
범주 → 범주 : 수치화 - 카이제곱검정
- 기대빈도 : 아무런 관련이 없을 때 나올 수 있는 빈도수
- 실제 데이터 : 관측도니 값들
카이 제곱 통계량 : 기대빈도와 실제 데이터의 차이
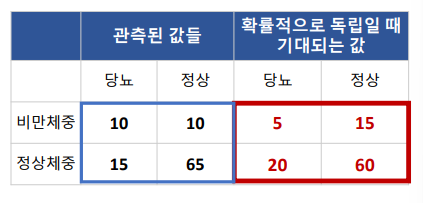
- 카이 제곱 통계량이 클수록, 기대 빈도로부터 실제 값에 차이가 크다는 의미
- 범주의 수가 늘어날 수록 값은 커지게 되어있음
- 자유도의 약 2배보다 크면, 차이가 있다고 봄.(관계가 있다)
범주형 변수의 자유도
- 범주의 수 - 1
- 카이제곱 검정에서 자유도 계산
- (x 변수의 자유도 ) * (y 변수의 자유도)
- ex) Pclass -> Survived
- Pclass: 범주 3개, Survived : 범주 2개
- (3-1) * (2-1) = 2
- (x 변수의 자유도 ) * (y 변수의 자유도)
카이 제곱 검정
- crosstab으로 검정
- 주의 : Normalize 옵션 사용 X
- 카이 제곱 검정 수행
# 1) 먼저 교차표 집계
table = pd.crosstab(titanic['Survived’],
titanic['Pclass'])
print(table)
print('-' * 50)
# 2) 카이제곱검정
spst.chi2_contingency(table)
결과
1. 카이제곱 통계량
2. p-value
3. 자유도 : Pclass자유도(3-1) * Survived 자유도 (2-1)
4. 기대빈도 : 계산된 값
6. 이변량 분석 : 숫자 -> 범주
시각화
sns.kdeplot( )
-
kdeplot( , hue = 'Survived')
:생존여부의 비율이 유지된 채로 그려짐- 두 그래프의 아래 면적의 합이 1
-
kdeplot( , hue = 'Survived', common_norm = False)
: 생존자, 사망자 각각 kde plot 그리기- 생존여부 각각 아래 면적의 합이 1인 그래프 (True일때는 두 그래프의 합이 1)
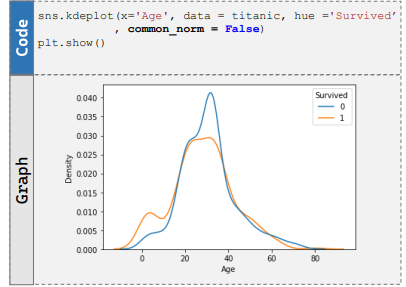
- 생존여부 각각 아래 면적의 합이 1인 그래프 (True일때는 두 그래프의 합이 1)
-
두 선이 만나는 지점 : 전체 평균과 같은 지점
hue='' : 특정 범주를 색상으로 구분
- kdeplot( , hue = 'Survived', multiple = 'fill')
: 모든 구간에 대한 100% 비율로 kde plot 그리기
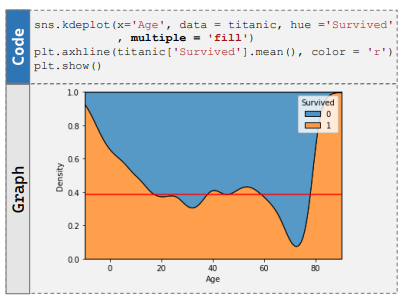
- x 축 : 나이
- y 축 : 비율
- 빨간 선 : 전체 생존률
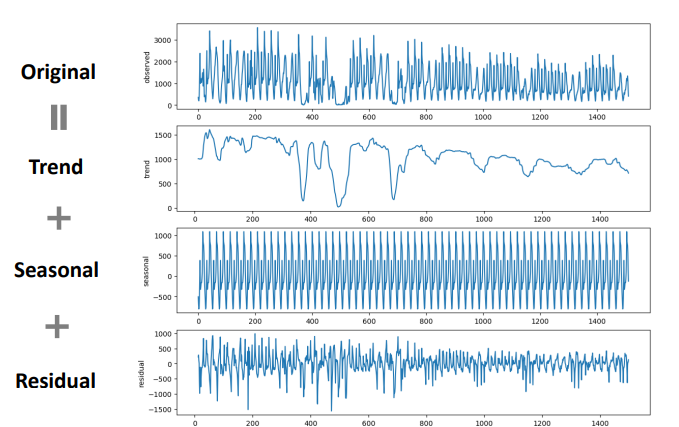
추가 : 시계열 데이터 분석 기초
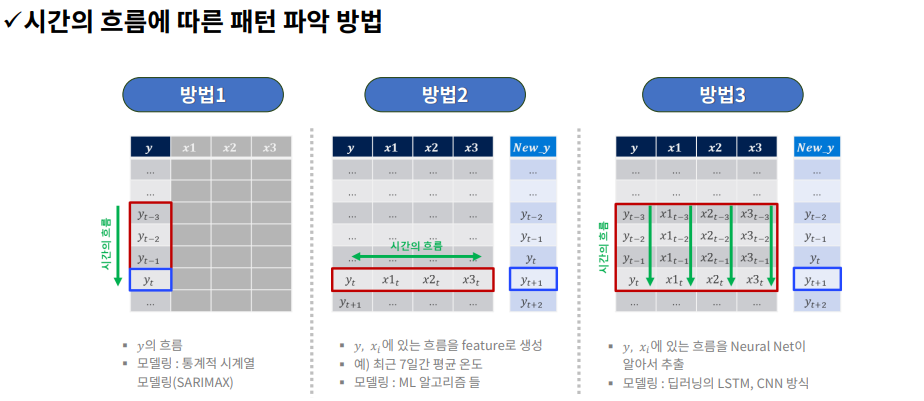
지금까지 시계열 데이터에 대한 처리는 방법2였음
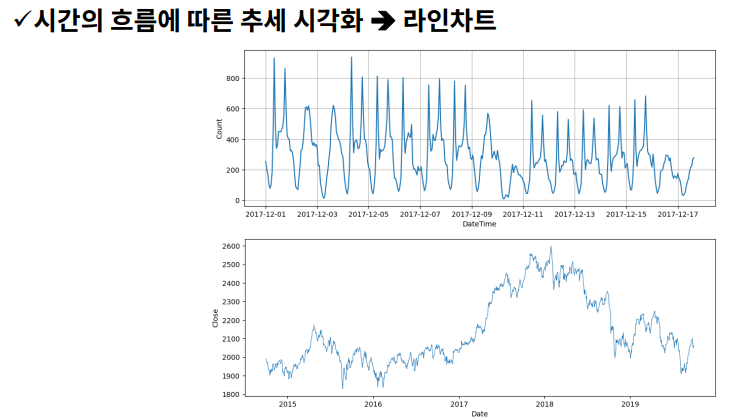
시간의 흐름에 따른 패턴 찾기
라인차트
시계열 데이터 분해
- 두가지 패턴 추출
- Trend : 추세 패턴
- Seasonal : 사이클(주기),계절성 패턴
- 문법
# 시계열 데이터 분해
decomp = sm.tsa.seasonal_decompose(bike['Count'], model = 'additive', period = 24)- period = 24
- Trend : window size = 24로, 이동평균 계산
- Seasonal : 원본에서 Trend를 빼고, 동일 주기(24)의 데이터 평균으로 계산
- 평균은 0(에 근사)
자기상관성
패턴을 데이터로 만들기
날짜 요소 추출
이전 데이터 만들기(.shift)
이동평균 만들기(.rolling)
차분 데이터(.diff)
복습 복습 복습