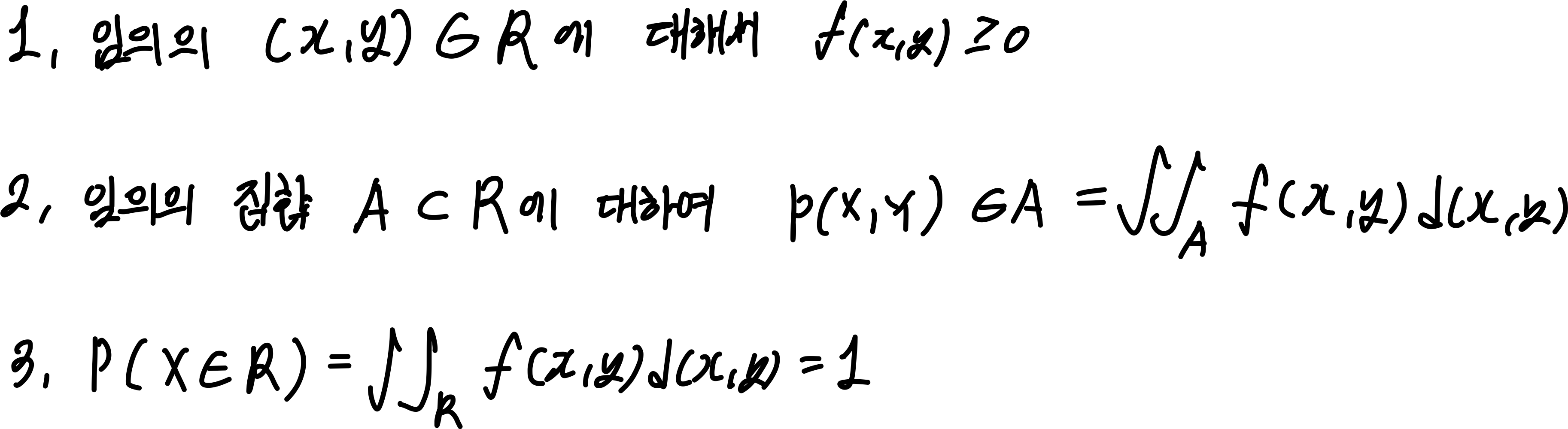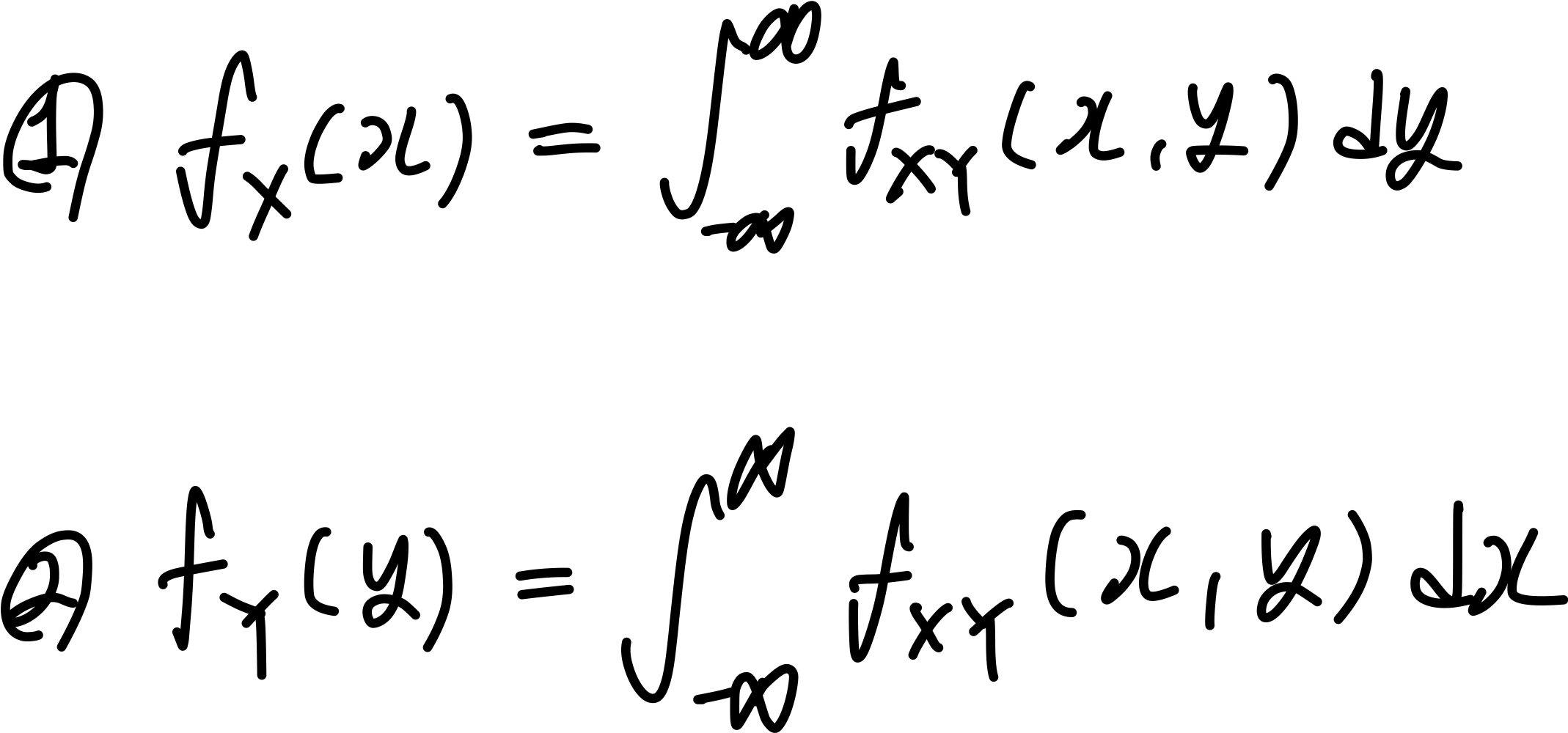[ 통계 ] Marginal Distribution

개요

지난 포스트에서 확률 변수와 확률 분포에 대해서 다루었다. 지난번까지 공부한 내용에서는 하나의 표본 공간에 하나의 확률 변수를 정의한 경우를 살펴봤었는데, 이번 포스트에서는 하나의 표본공간에 대해서 1개 이상의 확률변수를 정의한 경우에 대해서 공부하려고 한다.

결합확률밀도함수

예시

예를 들어 1개의 동전을 2회 던지는 실험을 생각해볼 수 있다. 앞면을 H, 뒷면을 T로 나타내면 우리가 정의할 수 있는 sample space, $S$ 는 $S = \{HH, HT, TH, TT\}$로 생각할 수 있고, sample space위에 2개의 확률변수 $X$와 $Y$를 다음과 같이 정의를 해보자.
$X : 첫 번째 시행에서 앞면이 나오면 0 뒷면이 나오면 1의 값을 가진다.$
$Y : 두 번째 시행에서 앞면이 나오면 0 뒷면이 나오면 1의 값을 가진다.$
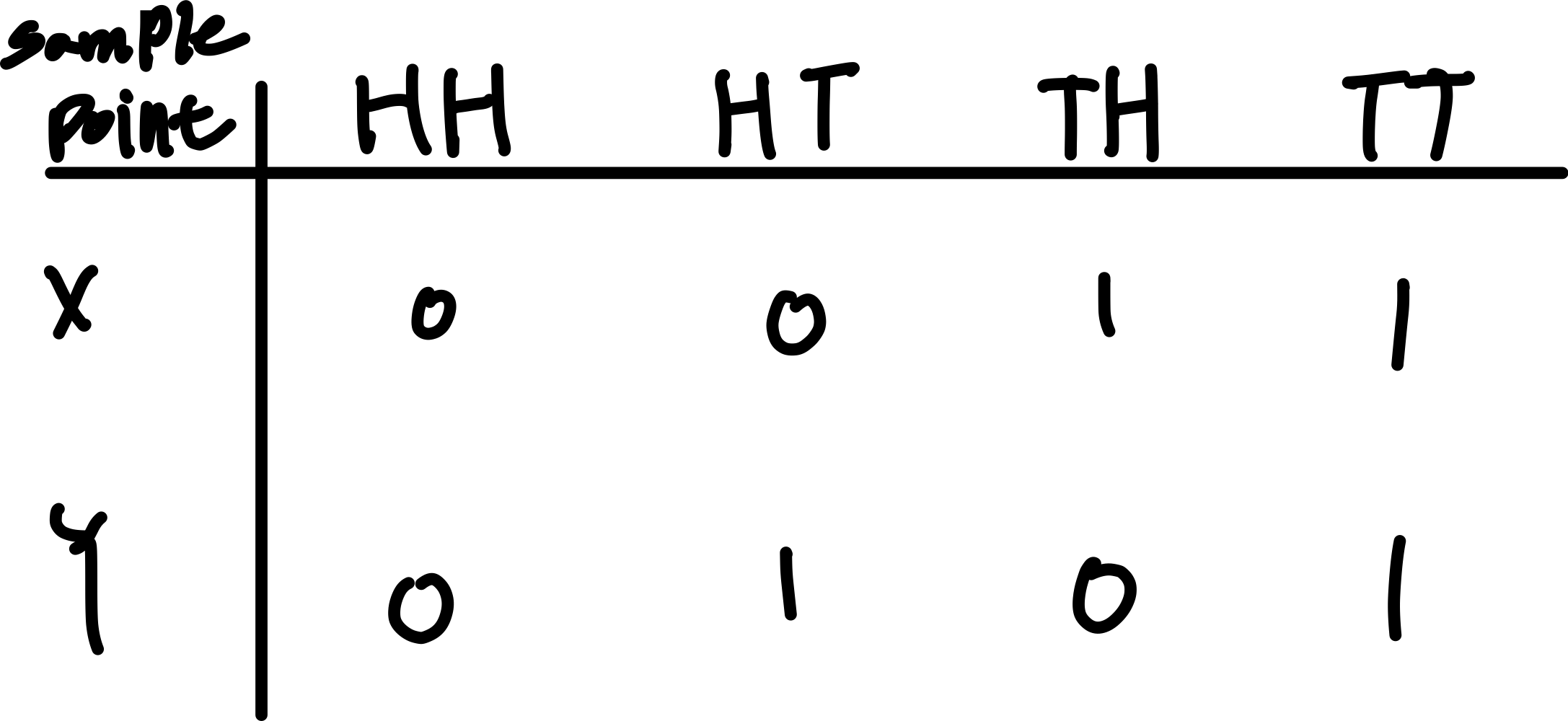
이렇게 정의하면 다음과 같이 X와 Y가 가질 수 있는 값은 각각 두 가지이고 각각의 값을 조합할 수 있는 방법은 총 네 가지이다.

따라서 '첫 번째 시행에서 앞면이 나오고 두 번째 시행에서 뒷면이 나올 확률'은 {HT}가 출현할 확률과 같고 이를 확률변수 X와 Y를 통해 나타내면 '$X=0 and Y=1$일 확률'이 된다.

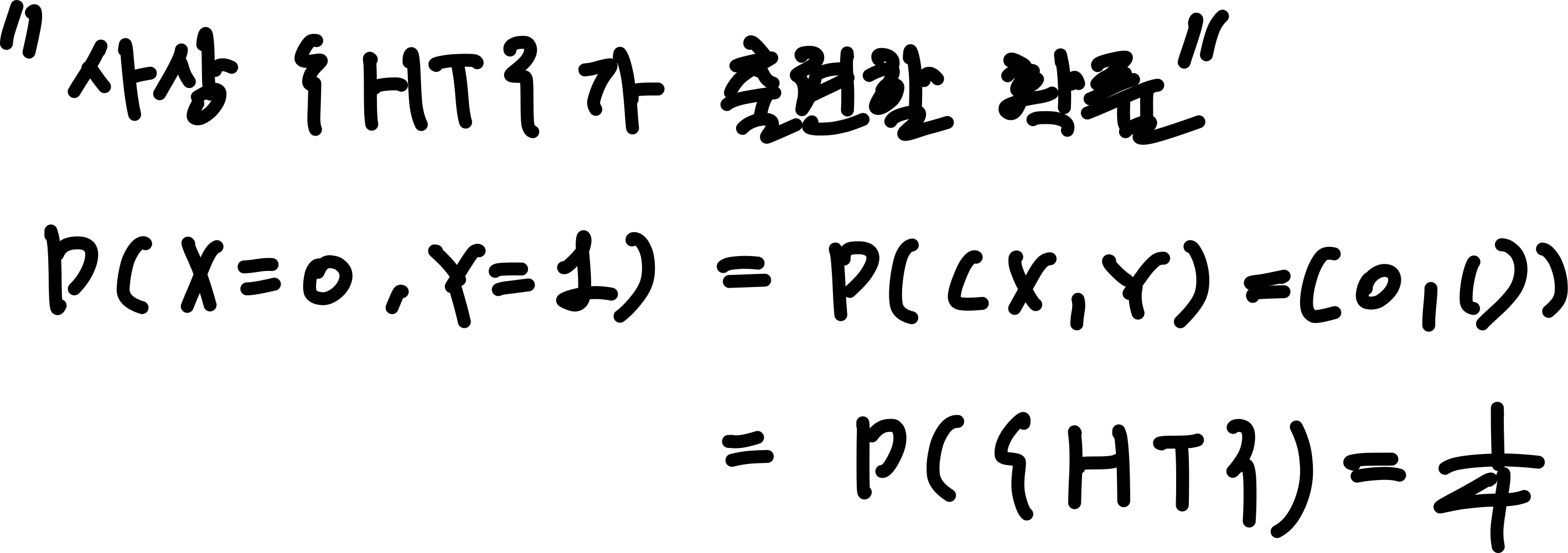
같은 방법으로 모든 경우의 확률을 계산하여 이를 표로 나타내면 각각을 X와 Y의 결합확률분포표라고 한다.

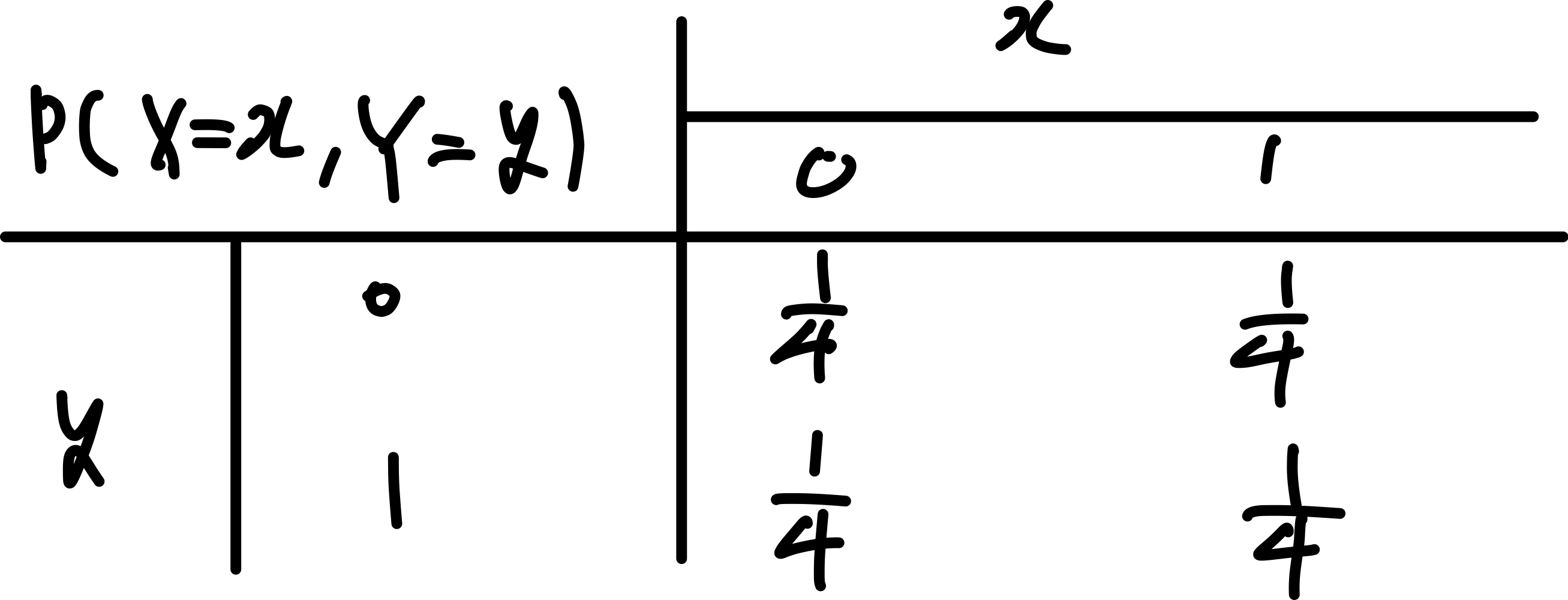
정의

위 예시에서 이산형 확률변수 X와 Y가 가질 수 있는 값 x와 y에 대하여 확률 P(X=x, Y=y)를 대응시켜 주는 함수 $f$를 이산형 결합확률밀도함수(discrete joint probability density function)라고 한다.
연속형 확률변수의 경우 연속형 결합확률밀도함수이다.

확률변수 X,Y가 집합 R에서 값을 가지는 연속형 확률변수이며, 이 구간 위에서 정의된 함수 $f$가 다음의 성질을 만족할 때, $f$를 X와 Y의 결합확률밀도함수 혹은 결합밀도함수라고 한다.

주변확률분포

확률변수 X와 Y의 결합밀도함수 $f_{XY}$가 주어지면 $f_{XY}$를 사용하여 X와 Y 각각의 확률밀도함수 $f_{X}$와 $f_{Y}$를 쉽게 구할 수 있다.

주변밀도함수(Marginal Probability Density Function)
확률변수 X,Y의 결합밀도함수가 $f_{XY}$일 때, X와 Y의 확률밀도함수 $f_{Y}$와 $f_{Y}$를 다음과 같이 구할 수 있고 이를 주변확률밀도함수(Marginal Probability Density Function)이라고 한다.