[딥러닝] CNN(Convolutional Neural Network)

CNN(Convolutional Neural Network)

CNN은 딥러닝에서 이미지와 영상 인식을 위해 사용되는 모델이다.
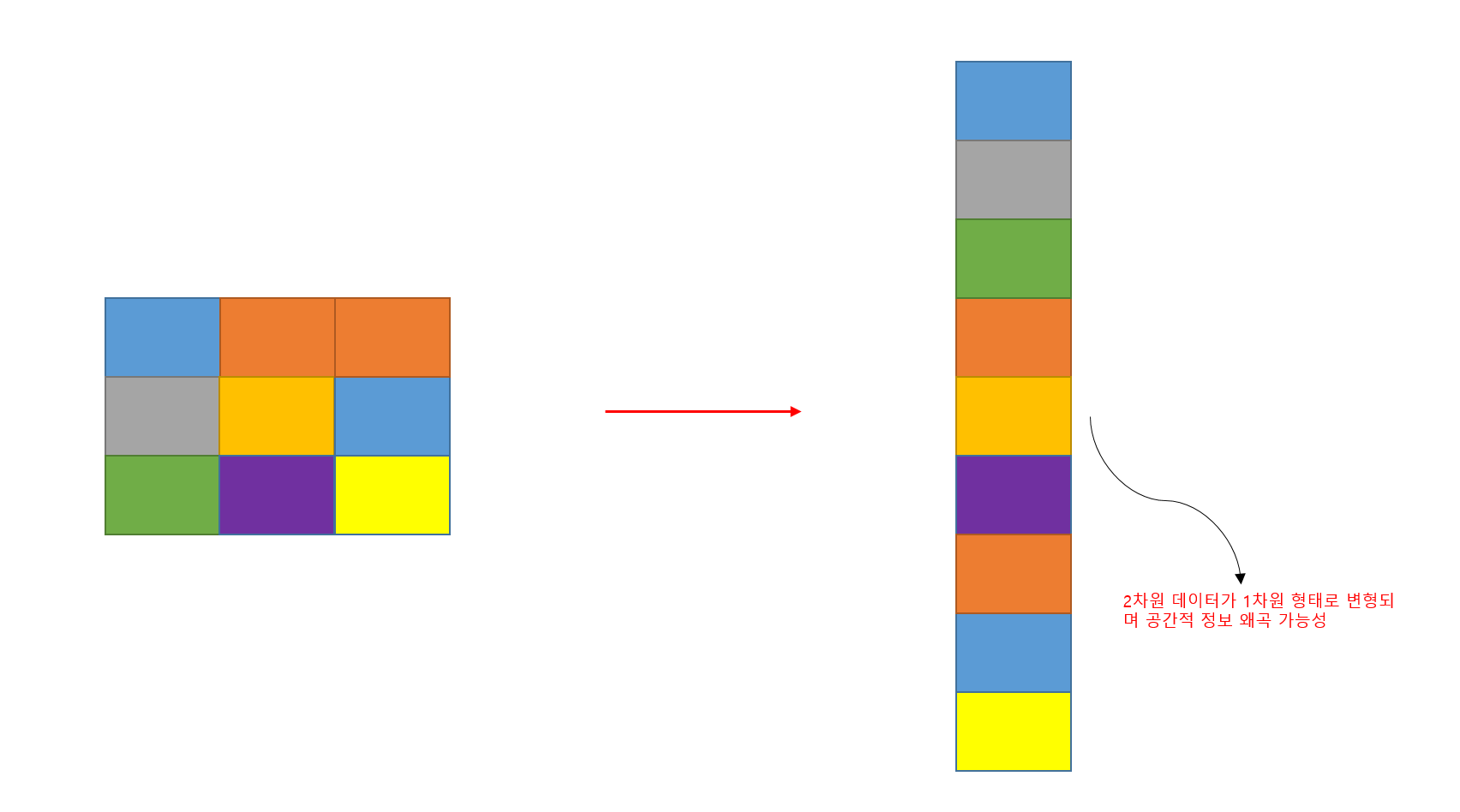
이미지와 영상 처리 분야에서는 기존의 밀집 신경망이 사용되기 힘들다. 1차원으로 데이터를 바꿔서 입력해야 하기 때문에 이미지가 가진 공간 정보가 왜곡될 가능성이 있기 때문이다. 그러므로 이미지 데이터를 다룰 때는 CNN 모델을 사용하는 것이 적절하다. 즉, CNN 모델을 이용하여 이미지와 영상의 공간적 정보를 유지하며 학습을 진행할 수 있다.
CNN 모델을 통해 이미지와 영상의 분류, 검출, 추적 등의 문제를 해결할 수 있다.

---

컨볼루션(Convolution) 연산

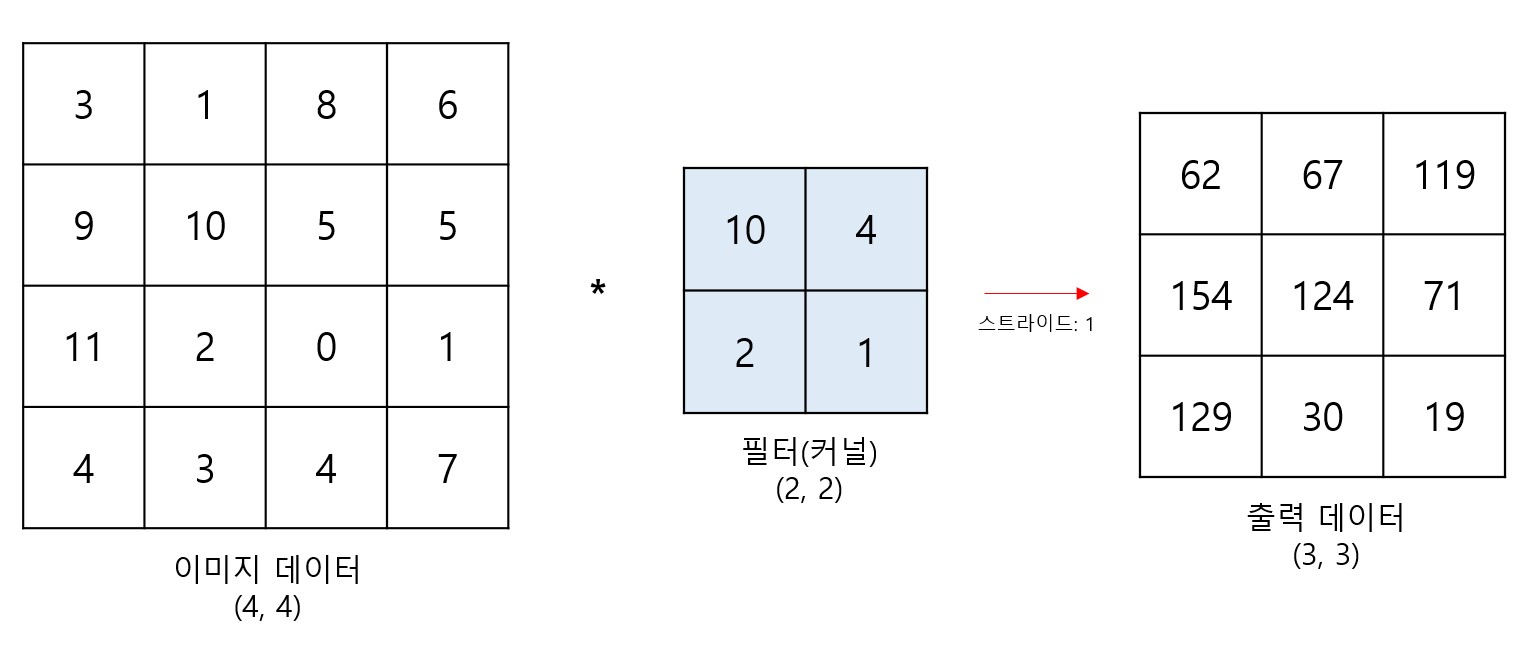
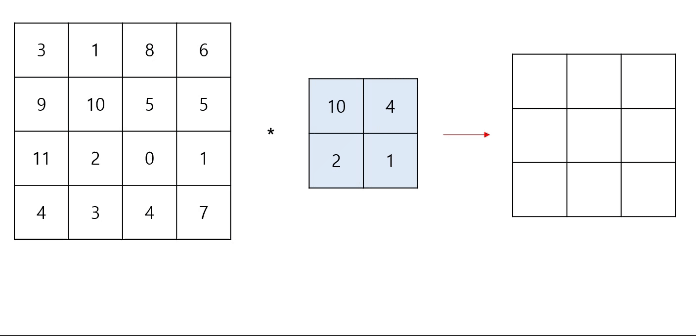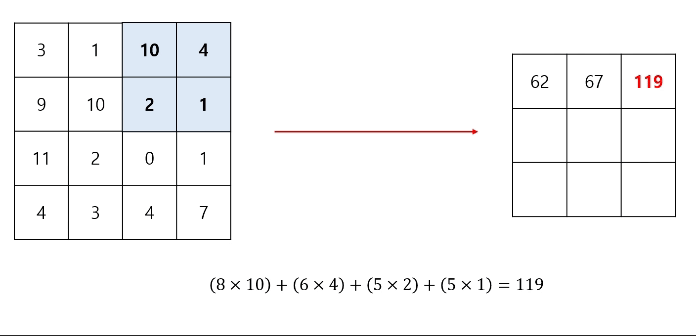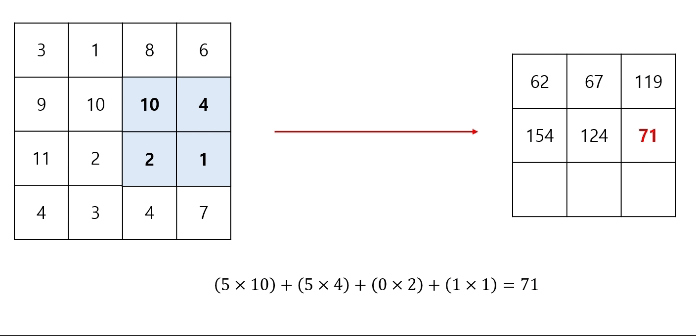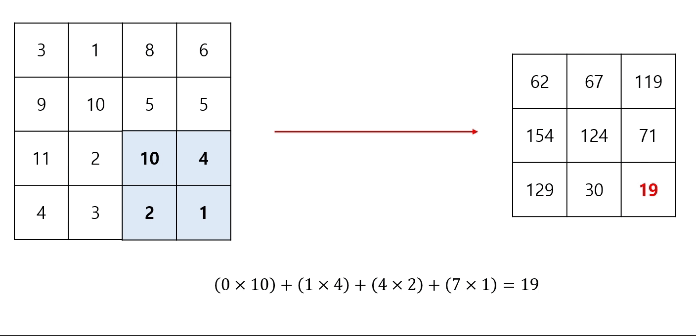
CNN 모델에서의 연산은 입력되는 이미지 데이터와 필터(커널)와의 컨볼루션 연산을 통해 이루어진다. 이때 CNN 모델의 핵심 아이디어는 이러한 연산과 학습을 통해 최적의 필터를 알아낸다는 것이다.


필터의 크기는 사용자가 임의로 설정할 수 있는 Hyper parameter이고, 이는 입력 데이터보다 커서는 안된다.
스트라이드(stride)는 컨볼루션 연산을 할 때 필터의 보폭을 얼마나 할지를 뜻하고, 만약 스트라이드가 1이라면 입력 이미지 데이터 위에서 필터는 한칸씩 이동하며 연산을 하게된다. 물론 스트라이드가 2이라면 2칸씩 이동하며 연산이 진행된다. 그만큼 출력 데이터의 차원은 더 작아지게 된다.

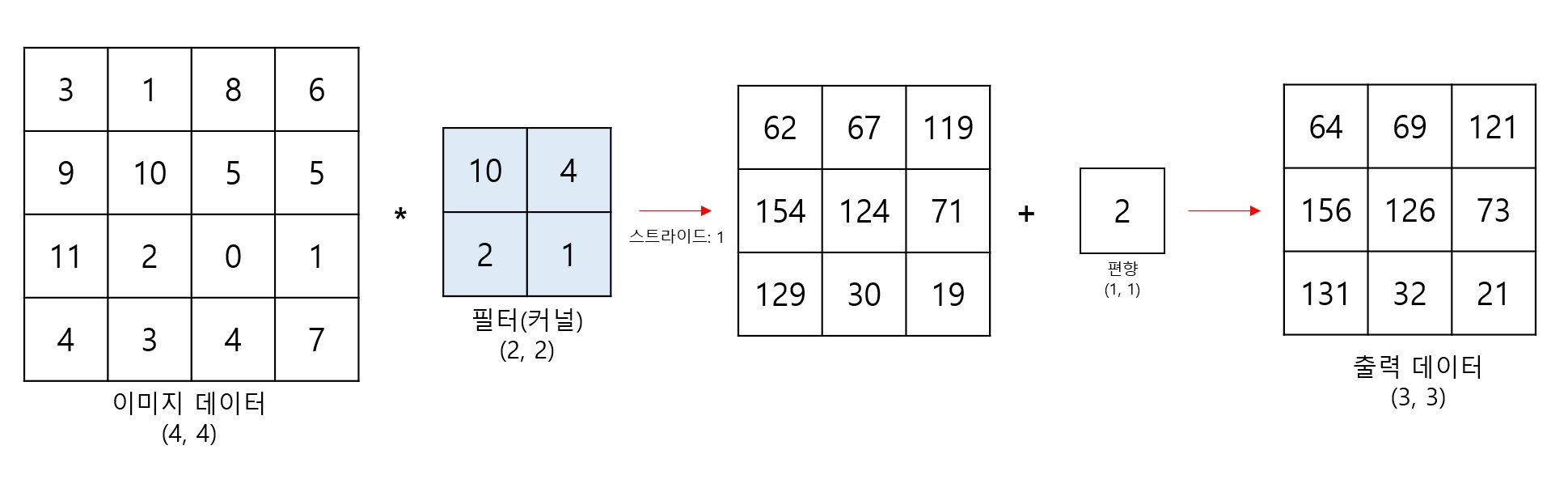
컨볼루션 연산 과정에 편향(bias)이 포함될 수도 있다.
편향의 shape는 (1, 1)이고, 필터 연산을 거친 출력의 각 성분에 동일하게 더해준다.

패딩(Padding)의 필요성

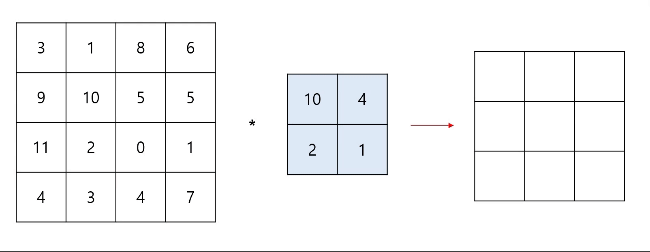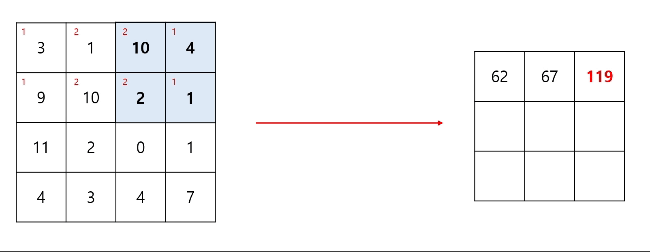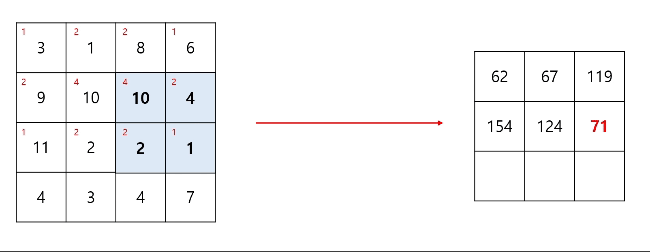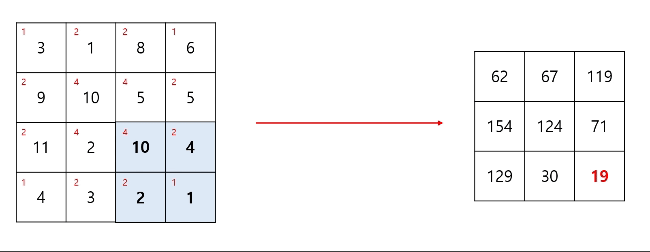
컨볼루션 연산이 진행되면 출력 데이터의 차원은 감소하게 된다. 출력 데이터의 차원은 입력 데이터의 차원, 필터의 차원, 스트라이드의 크기, 패딩의 여부에 따라 달라지게 된다. 이와 관련된 식은 이후에 소개하겠다.
패딩을 적용하면, 출력 데이터의 크기가 너무 작아지는 문제를 방지할 수 있고, 입력 데이터의 가장자리에 있는 정보가 소실되는 문제 또한 방지할 수 있다.
위 이미지에서 볼 수 있는 것 처럼, 패딩을 적용하지 않는다면 가장자리 데이터는 컨볼루션 연산 과정 중에 1번 밖에 관여되지 않는다는 것을 확인할 수 있다. 이는 가장자리에 중요한 데이터가 포함되는 경우에 학습 효율에 악영향을 끼칠 수 있다.

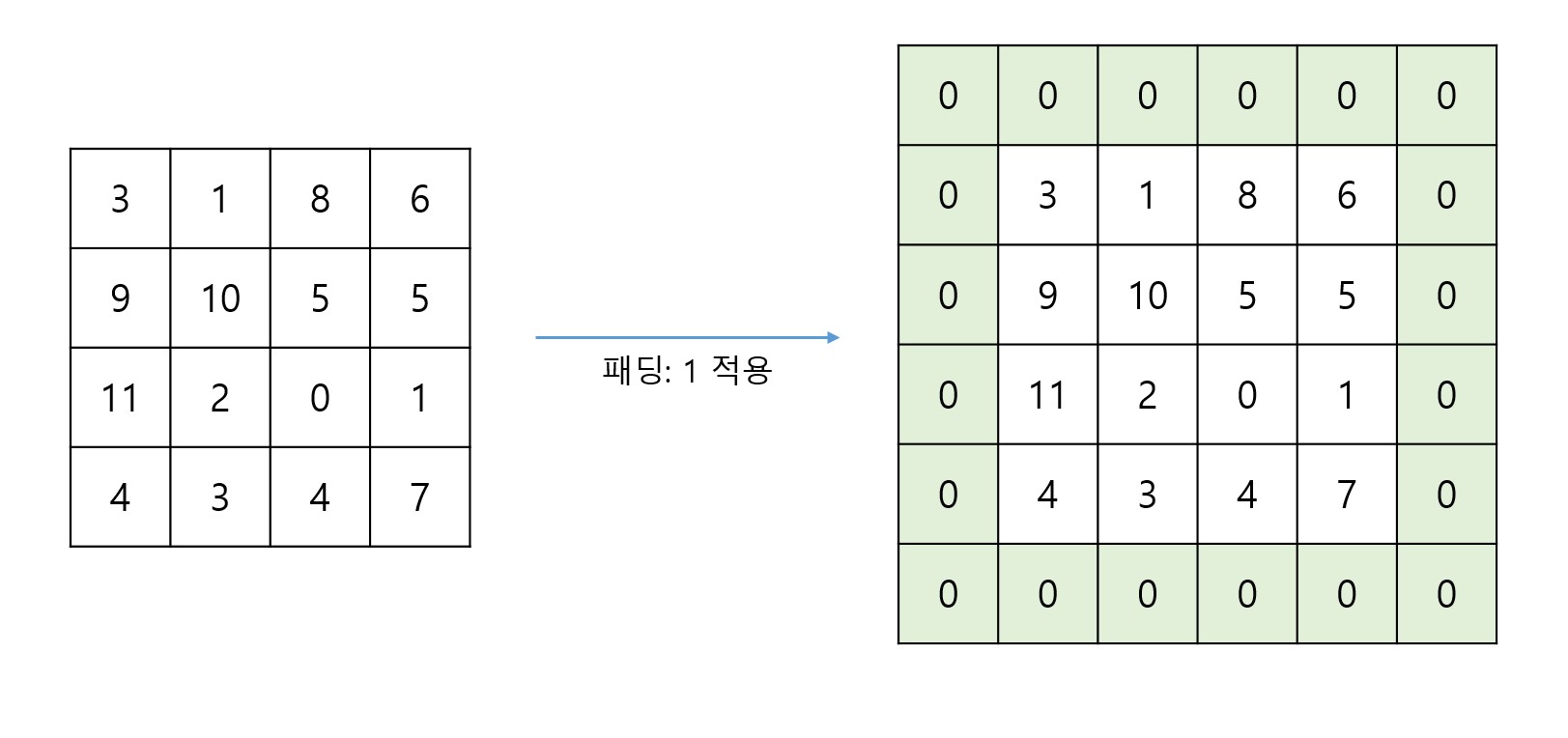
위 이미지 처럼 패딩을 1칸 적용한다고 가정하면, 합성곱 연산을 거치기 전에 입력 데이터 주변을 특정 값(보통 0)으로 1칸 만큼 적절히 채워넣는 것이다. 물론 2칸을 적용한다고 하면 특정 값으로 2칸 만큼 적절히 채워넣으면 된다.
이렇게 패딩 처리를 하면 출력 데이터의 크기가 지나치게 감소하는 문제를 해결할 수 있고, 입력 데이터의 가장자리와 내부 픽셀은 동일한 횟수의 필터 연산을 거치게 된다.

출력 차원 계산

$H_{out}$ : 출력 데이터의 높이
$H_{in}$ : 입력 데이터의 높이
$H_{filter}$ : 필터의 높이
$W_{out}$ : 출력 데이터의 너비
$W_{in}$ : 입력 데이터의 너비
$W_{filter}$ : 필터의 너비
$S$ : 스트라이드(Stride)
$P$ : 패딩(Padding)

ex) 입력 데이터: (5, 5), 필터: (2, 2), 스트라이드: 1, 패딩: 1
=>$H_{out} = \frac{5 + (2\times1) - 2}{1} + 1 = 6$, $W_{out} = \frac{5 + (2\times1) - 2}{1} + 1 = 6$

입력 데이터의 채널이 2개 이상일 때

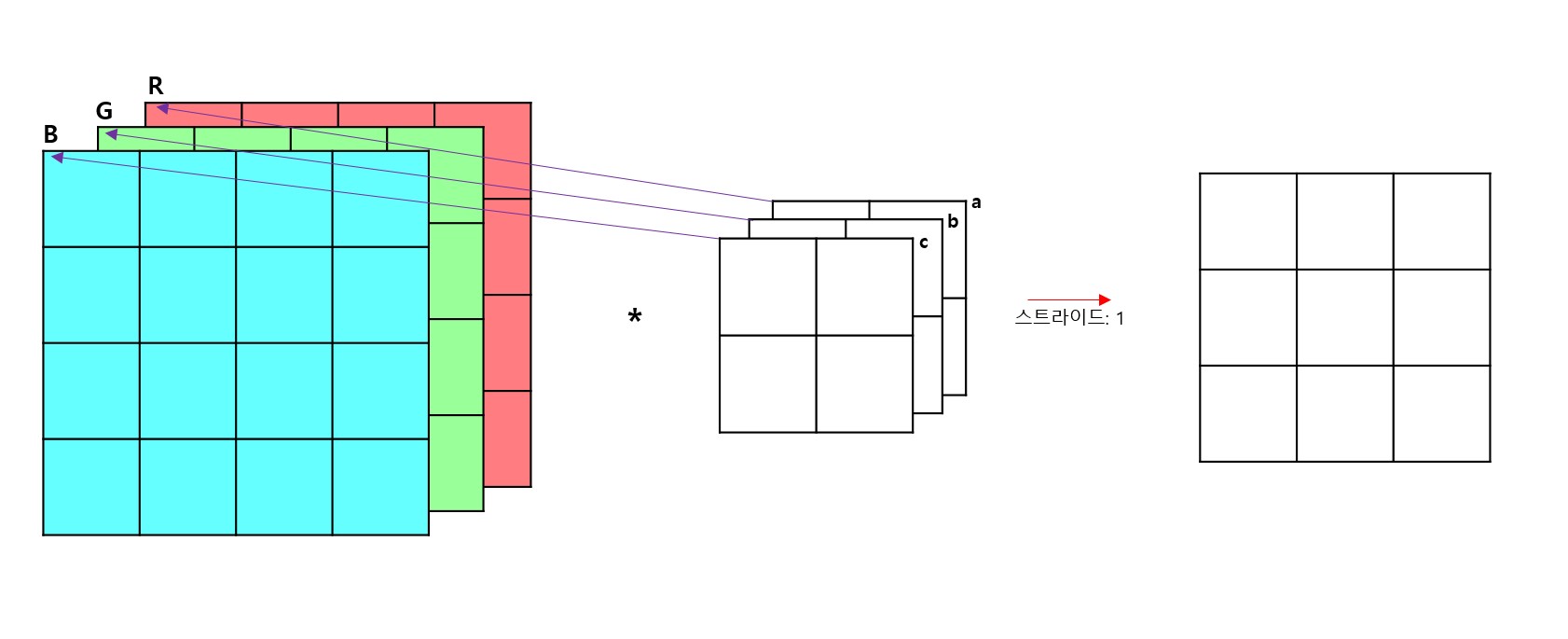
입력되는 데이터의 채널이 2개 이상인 경우에는 그 채널 수에 맞게 필터의 수도 늘어나게 된다. 즉, Input data의 채널 수와 filter의 채널 수는 같아야 한다.
위 사진처럼 채널의 개수가 3개인 RGB 이미지가 입력으로 들어올 때, 필터의 채널 수도 abc로 3개이다.
입력 데이터의 R 채널은 필터의 a 채널, 입력 데이터의 G 채널은 필터의 b 채널, 입력 데이터의 B 채널은 필터의 c 채널과 컨볼루션 연산이 이루어진다.
위 연산을 통해 도출된 3개의 결과를 각 픽셀별로 더해 하나의 채널을 가진 출력 데이터로 나오게 된다.

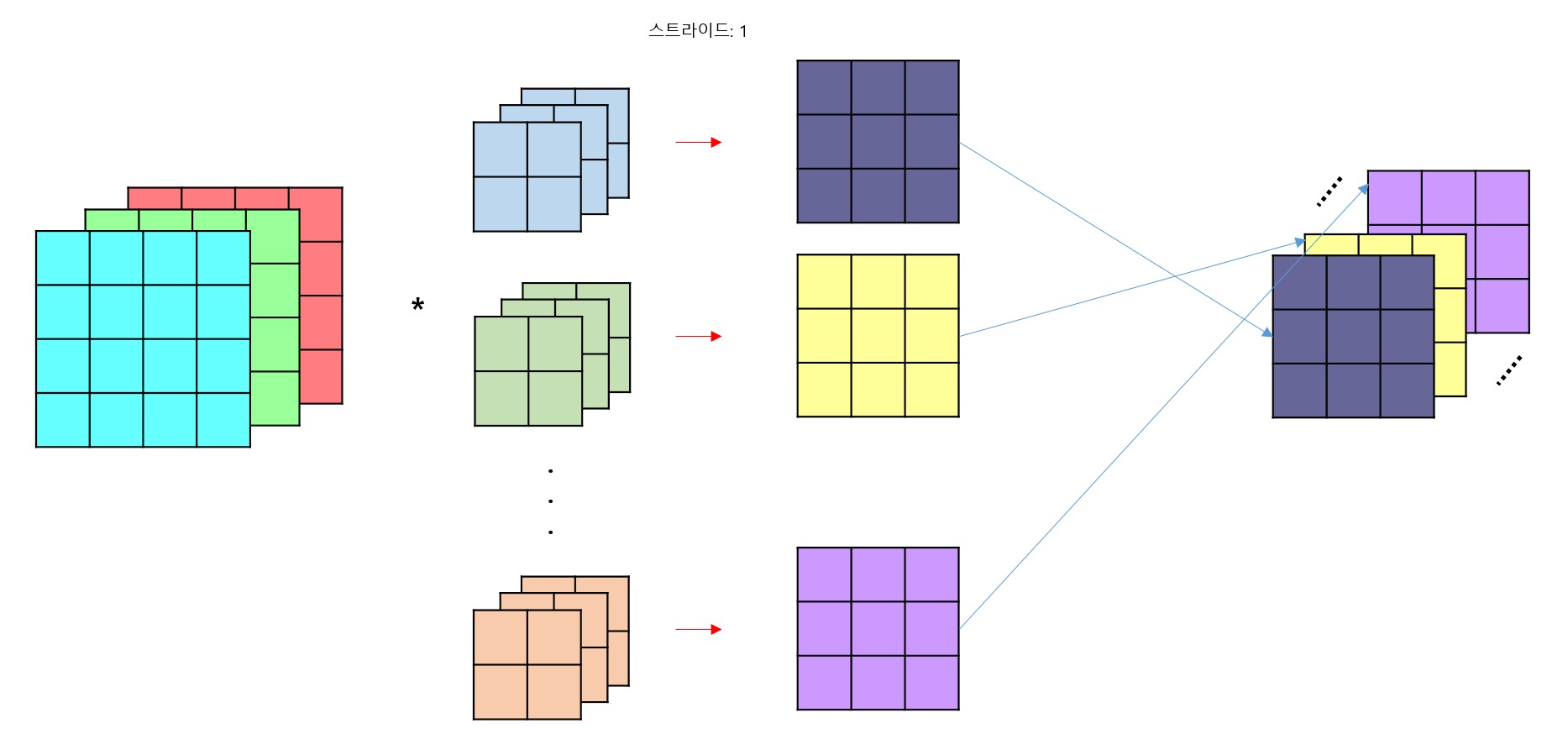
출력 데이터의 채널 개수를 늘리기 위해선 그만큼 필터의 개수를 늘려주면 된다.
위 사진처럼, Input data의 channel 수와 관계 없이 filter의 개수만큼 output data가 나오게 된다. 즉,

입력층에 대해 사용한 필터 수 = 출력층의 채널 수

이다.
CNN 모델에서는 하나의 Layer의 출력이 다음 Layer의 입력이 되는 형태이므로 필터 수를 통해 채널 수를 잘 맞춰주어야 한다.

---

풀링(Pooling) 연산

풀링계층은 데이터의 크기를 줄이기 위해 사용되는 층이고, 별도의 학습은 일어나지 않는다.
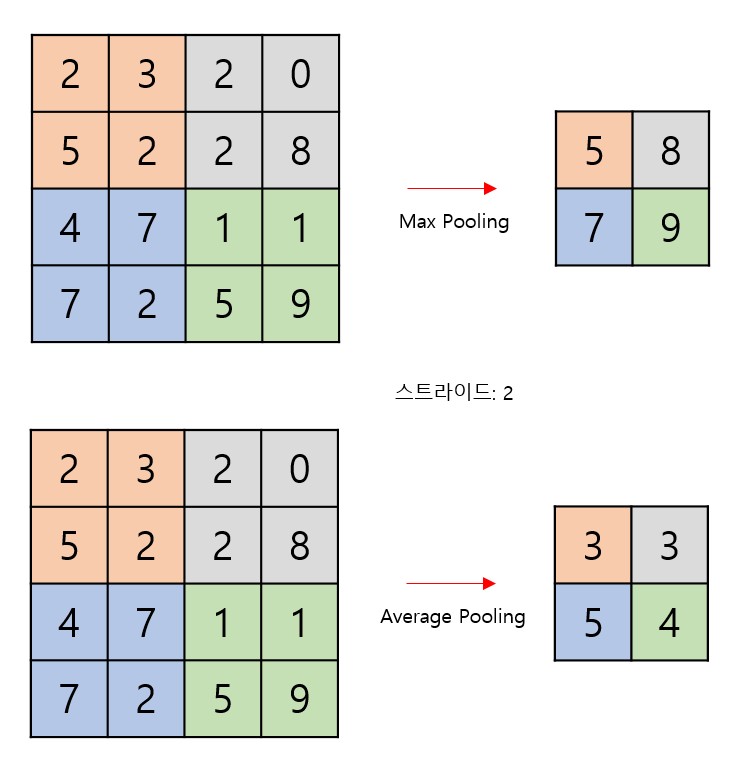
풀링의 종류에는 크게 Max Pooling, Average Pooling이 있다.

Max Pooling: 풀링 영역의 최댓값 출력
Average Pooling: 풀링 영역의 평균값 출력

입력 채널이 여러 개인 경우에는 각 채널에 대해 독립적으로 풀링 연산을 진행한다.

출력 차원 계산

$H_{out}$ : 출력 데이터의 높이
$H_{in}$ : 입력 데이터의 높이
$H_{filter}$ : 필터의 높이
$W_{out}$ : 출력 데이터의 너비
$W_{in}$ : 입력 데이터의 너비
$W_{filter}$ : 필터의 너비
$S$ : 스트라이드(Stride)

---

CNN 모델 개요도

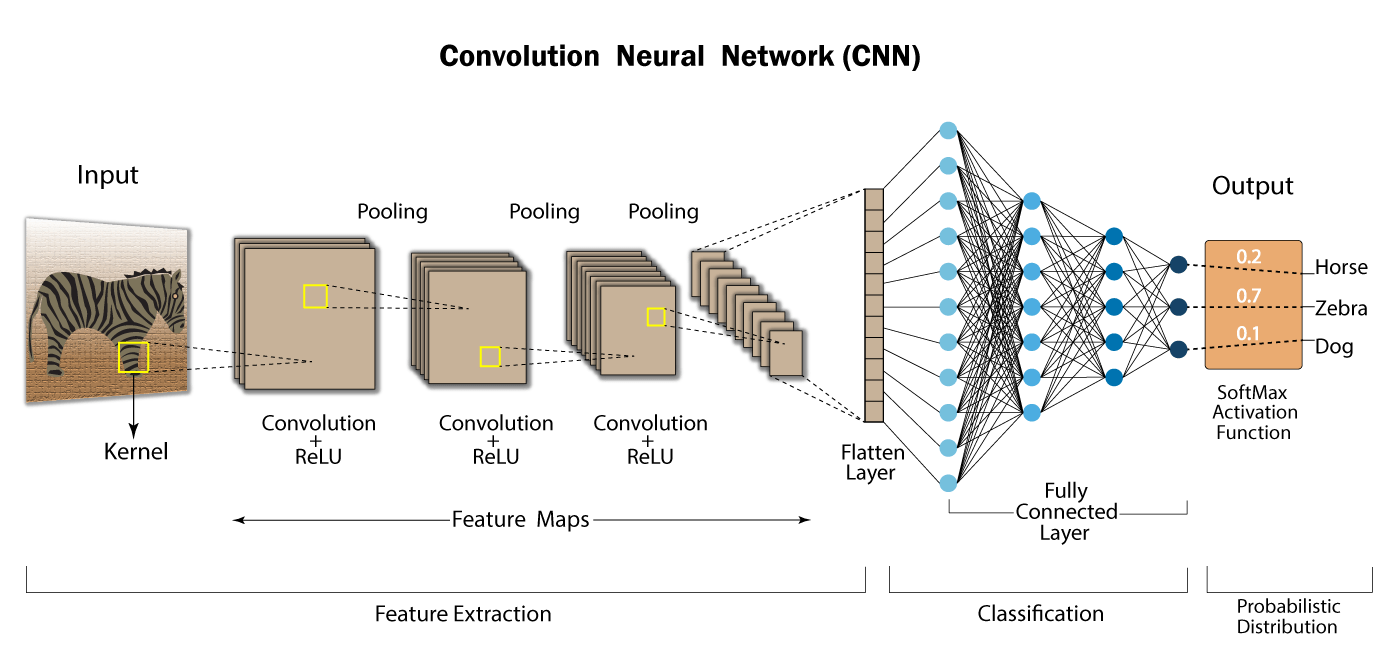
입력 데이터가 Convolution 계층, 활성화 함수, Pooling 계층을 차례로 통과하게 된다.
이 Convolution 계층 + 활성화 함수 + Pooling 계층들을 지나면서 입력 데이터의 특징이 추출된다.

마지막 Pooling 계층까지 통과한 데이터가 최종 목표인 Classification을 수행하기 위해서는 밀집층(Fully Connected Layer)에 입력되어야 한다.
밀집층에 입력되기 전에, 이 2차원 형태의 데이터를 1차원 형태로 벡터화 하는 Flatten 과정이 필요하다.
1차원 벡터 형태의 데이터가 밀집층에 입력이 되면, 최종 분류 작업이 수행되게 된다.

이 전체 CNN 모델에서는 Loss function, Optimizer를 통해 모델을 평가하면서, 모델 파라미터인 필터와 밀집층의 가중치(W)와 편향(b)이 갱신되게 된다.