[Pytorch] Seq2Seq 모델 구현

wh·2024년 8월 27일
DLPyTorchRNNSeq2Seq딥러닝
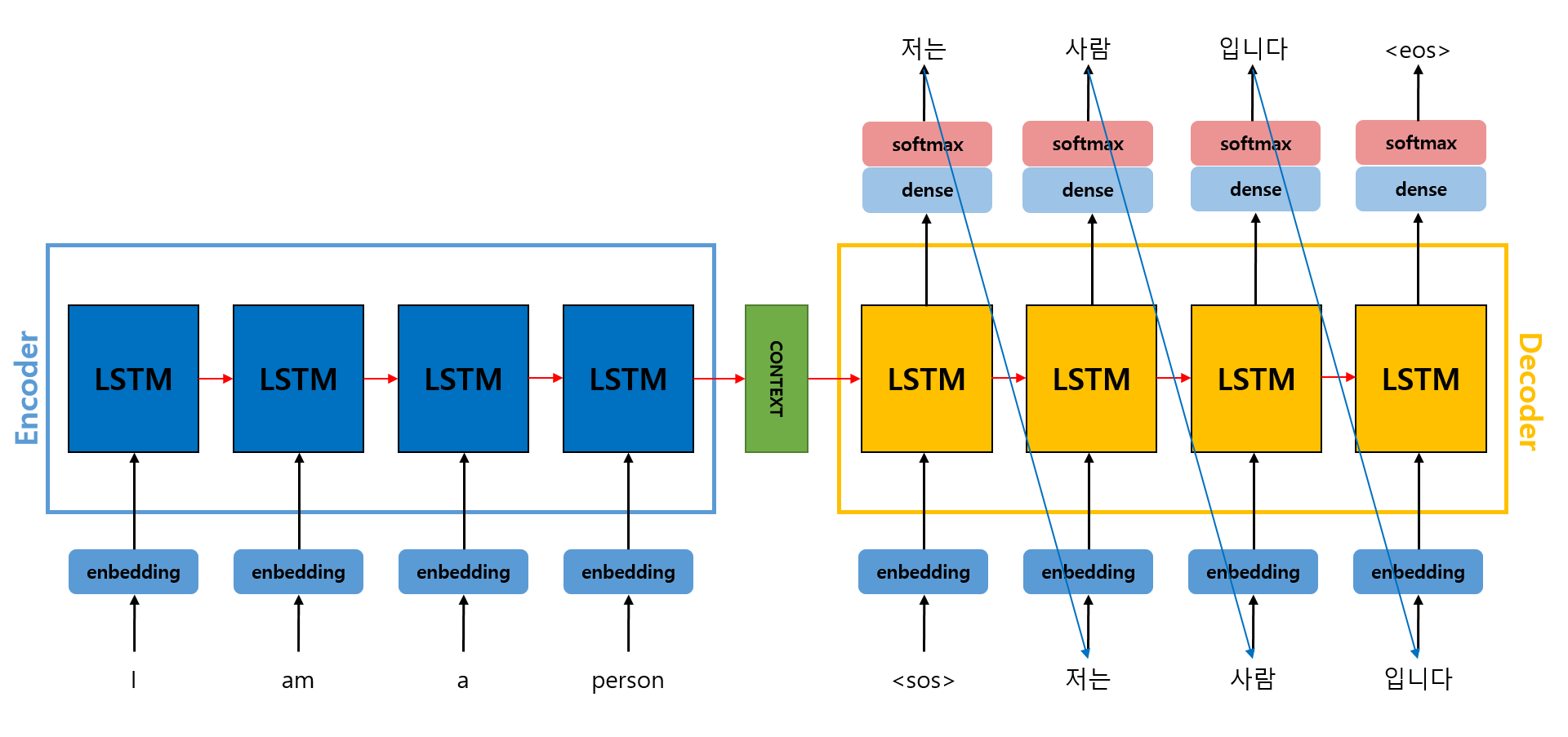
post-thumbnail

Seq2Seq 모델 구현

Pytorch를 통해 Seq2Seq 모델을 구현해볼 것이다.
RNN 모델을 구현했을 때 처럼 이번에도 직접 함수를 만들어 데이터셋을 생성할 것이다. 우선 어떤 데이터셋을 사용할 것이며, Seq2Seq 모델을 이용하여 무슨 목적을 달성할 것인지 설명하겠다.

Dataset

이번에도 수열 데이터를 이용할 것이다. 모델 구현 후 만약 모델의 Encoder에 [1,2,3,4,5][1, 2, 3, 4, 5]라는 수열이 입력된다면, Decoder에는 이와 반대로 [5,4,3,2,1][5, 4, 3, 2, 1]이 출력되도록 목표를 정할 것이다. 물론 직접 입력되는 수열은 [1,2,3,4,5][1, 2, 3, 4, 5] 형태가 아닌 One-hot Encoding된 수열 형태이다. 그리고 이번에는 <sos><sos>, <eos><eos> 토큰 구현을 위해 (1,12)(1,12) 형태로 형성되도록 할 것이다. <sos><sos> 토큰은 11번째 원소에 할당할 것이며, <eos><eos> 토큰은 12번째 원소에 할당할 것이다. 예시는 아래와 같다.

0 => [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
1 => [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
2 => [0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
3 => [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
.
.
.
9 => [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0]
sos => [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
eos => [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]

함수 구현에 앞서, 우선 필요한 것들을 import 해주겠다.

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

import numpy as np

import matplotlib.pyplot as plt
%matplotlib inline

from collections import defaultdict
  
from IPython.display import clear_output

이후 함수를 구현한다.

def generate_data(seq_length_min=1, seq_length_max=20, batch_size=10):
    T = np.random.randint(seq_length_min, seq_length_max + 1)
    x = np.random.randint(0, 10, (T, batch_size))
    one_hot_x = np.zeros((T + 1, batch_size, 12), dtype=np.float32)
    one_hot_x[np.arange(T).reshape(-1, 1), np.arange(batch_size), x] = 1
    one_hot_x[-1, :, -1] = 1
    ends = np.full(batch_size, 11).reshape(1, -1)
    y = np.concatenate([x[::-1], ends], axis=0)
    return x, one_hot_x, y

함수를 설명하기에 앞서, 이번 포스트에서는 데이터들을 batch 단위로 처리할 것임을 알린다. 즉, 여러 수열들이 batch_size 만큼 묶인 형태로 데이터셋을 생성할 것이다.



def generate_data(seq_length_min=1, seq_length_max=20, batch_size=10):

'generate_data'라는 함수를 정의한다. 만들어질 수 있는 수열의 최소 길이는 1, 최대 길이는 20으로 설정한다. batch_size는 10으로 가정한다. 이들은 꼭 이 값들로 정해져야 하는 건 아니고, 사용자가 임의로 설정할 수 있는 Hyper parameter이다.

T = np.random.randint(seq_length_min, seq_length_max + 1)

T(수열 길이)를 1 이상, 21 미만의 정수들 중 random하게 설정한다.

x = np.random.randint(0, 10, (T, batch_size))

random하게 설정된 T와 기존에 설정된 batch_size를 기준으로 (T, batch_size)의 형태를 가지는 배열을 생성한다. 이때 배열의 원소들은 0부터 9까지 원소 중 random하게 설정한다. 만약 T가 4로 설정되었다면 생성되는 배열은 아래와 같다.



array([[5, 1, 4, 9, 4, 4, 5, 1, 3, 3],
       [8, 6, 4, 2, 0, 7, 6, 2, 3, 4],
       [9, 2, 5, 2, 3, 4, 7, 3, 5, 4],
       [6, 4, 1, 1, 2, 0, 1, 8, 9, 5]])
one_hot_x = np.zeros((T + 1, batch_size, 12), dtype=np.float32)

One_hot Encoding된 배열 x를 담기 위한 3차원 배열을 형성하고, 모든 원소들의 값을 0으로 초기화 해준다. T가 아니라 T + 1인 이유는 <eos><eos> 토큰이 One_hot Encoding된 형태를 담아주기 위해서이다. 예시는 아래와 같다.



array([[[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]],

       [[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]],

       [[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]],

       [[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]],

       [[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]]], dtype=float32)
one_hot_x[np.arange(T).reshape(-1, 1), np.arange(batch_size), x] = 1

이제 초기화된 one_hot_x 배열에 기존에 생성한 x배열에 맞게 One_hot Encoding 해준다. 이때 one_hot_x의 shape는 (T+1, batch_size, 12)이고, x의 shape는 (T, batch_size)이므로 one_hot_x의 마지막 block은 모두 0으로 채워져 있을 것이다.



array([[[0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.], <= 5
        [0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 1
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], <= 4
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.], <= 9
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], <= 4
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], <= 4
        [0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.], <= 5
        [0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 1
        [0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.], <= 3
        [0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.]],<= 3

       [[0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0.], <= 8
        [0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0.], <= 6
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], <= 4
        [0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 2
        [1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 0
        [0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0.], <= 7
        [0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0.], <= 6
        [0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 2
        [0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.], <= 3
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.]],<= 4

       [[0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.], <= 9
        [0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 2
        [0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.], <= 5
        [0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 2
        [0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.], <= 3
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], <= 4
        [0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0.], <= 7
        [0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.], <= 3
        [0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.], <= 5
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.]],<= 4

       [[0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0.], <= 6
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], <= 4
        [0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 1
        [0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 1
        [0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 2
        [1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 0
        [0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 1
        [0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0.], <= 8
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.], <= 9
        [0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.]],<= 5

       [[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]]], dtype=float32)

Block의 개수는 5개로, 기존의 수열의 길이(4)에 <eos><eos>의 One_hot Encoding 형태 저장을 위해 1을 더해준 것이다.
Block 내에서 세로 방향의 길이는 10으로, batch_size를 의미하고, 가로 방향은 12로, One_hot Encoding 벡터 수이다.

one_hot_x[-1, :, -1] = 1

이제 마지막 block에 <eos><eos> 토큰이 One_hot Encoding된 형태를 채워넣을 것이다.



array([[[0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.], <= 5
        [0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 1
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], <= 4
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0.], <= 9
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], <= 4
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], <= 4
        [0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0.], <= 5
        [0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 1
        [0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.], <= 3
        [0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.]],<= 3

       [[0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0.], <= 8
        [0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0.], <= 6
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.], <= 4
        [0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 2
        [1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 0
        [0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0.], <= 7
        [0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 0., 0.], <= 6
        [0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0.], <= 2
        [0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0.], <= 3
        [0., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0.]],<= 4
								 .
       							 .
								 .
  								 .
  								 .
       [[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.],
        [0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]]], dtype=float32)
ends = np.full(batch_size, 11).reshape(1, -1)

batch_size(10) 만큼의 원소 개수를 가지는 배열 ends를 만들어 줄 것이다. 이때 원소들의 값은 모두 11이다.
reshape(1,-1)을 통해 하나의 행만을 가지는 형태로 만들어준다.



array([[11, 11, 11, 11, 11, 11, 11, 11, 11, 11]])
y = np.concatenate([x[::-1], ends], axis=0)
return x, one_hot_x, y

concatenate를 통해 x를 axis=0 방향으로 반전시킨 후, axis=0 방향으로 ends를 붙여준다. 그 후 x, one_hot_x, y를 return한다.



array([[ 6,  4,  1,  1,  2,  0,  1,  8,  9,  5],
       [ 9,  2,  5,  2,  3,  4,  7,  3,  5,  4],
       [ 8,  6,  4,  2,  0,  7,  6,  2,  3,  4],
       [ 5,  1,  4,  9,  4,  4,  5,  1,  3,  3],
       [11, 11, 11, 11, 11, 11, 11, 11, 11, 11]])

보다시피 가장 아래 행에 <eos><eos> 토큰을 뜻하는 원소들을 붙여준 것을 알 수 있다.
여기서 의구심이 들 수도 있다. 이렇게 함수를 구현해서도 단순하게 기존 x를 반전시킬 수 있기 때문이다. 하지만 우리의 주 목적은 함수 구현이 아닌 수열을 반전시킬 수 있게 모델을 학습하는 것이기 때문에 다음 단계로 계속 나아가보겠다.

Model 구현, 정의

Seq2Seq 모델 구현을 위해서는 RNN 혹은 LSTM 모델 또한 구현해주어야 한다. 이번 포스팅에서는 RNN 모델을 구현해보겠다. 

class RNN(nn.Module):
    def __init__(self, dim_input, dim_recurrent, dim_output):
        super(RNN, self).__init__()

        """
        dim_input: C
        dim_recurrent: D
        dim_output: K
        """

        self.x2h = nn.Linear(dim_input, dim_recurrent)
        self.h2h = nn.Linear(dim_recurrent, dim_recurrent, bias=False)
        self.h2y = nn.Linear(dim_recurrent, dim_output)
        self.relu = nn.ReLU()

    def forward(self, x, h_t=None):

        """
        x: shape = (T, N, C)
        W_x: shape = (C, D)
        초기 h: shape = (1, N, D)
        W_h: shape = (D, D)

        => x X W_x: (T, N, C) X (C, D) = (T, N, D)
           (초기 h) X W_h: (1, N, D) X (D, D) = (1, N, D)  
           
           h: (T, N, D) + (1, N, D) = (T, N, D) broadcasting

        w_y: shape = (D, K)

        y: h X w_y
         = (T, N, D) X (D, K) = (T, N, K)  

        y: shape = (T, N, K)
        h: shape = (T, N, D)  
        """
        N = x.shape[1]
        D = self.h2h.weight.shape[0]


        # 초기 hidden state를 (1, N, D) shape의 0텐서로 설정
        if h_t is None:
            h_t = torch.zeros(1, N, D, dtype=torch.float32)

        h = []

        for i in range(x.shape[0]):
            h_t = self.x2h(x[i]) + self.h2h(h_t)
            h_t = self.relu(h_t)
            h.append(h_t)

        # 리스트 h에 저장된 모든 hidden state들을 dim=0 방향으로 합치기
        all_h = torch.cat(h, dim=0)

        all_y = self.h2y(all_h)

        return all_y, all_h

그후 Seq2Seq 모델을 구현한다.



class Seq2Seq(nn.Module):
    def __init__(self, dim_input, dim_recurrent, dim_output):
        super(Seq2Seq, self).__init__()

        """
        dim_input: 입력 데이터 차원(C)
        dim_recurrent: hidden state 차원(D)
        dim_output: 디코더 출력 차원(K)
        """

        self.encoder = RNN(dim_input, dim_recurrent, dim_output)
        self.decoder = RNN(dim_input, dim_recurrent, dim_output)

    def forward(self, x):
        """
        x(각 시퀀스에 대한 one-hot Encoding 입력): shape = (T, N, C)
        y(각 시퀀스의 디코딩된 출력): shape = (T, N, K)
        """
        T, N, C = x.shape

        y = []

        # 인코더를 통해 hidden state를 받음, 인코더의 출력은 취급하지 않음
        _, enc_h = self.encoder(x)

        # 마지막 step에서의 hidden state를 지정
        h_t = enc_h[-1:]

        # <sos> 토큰 즉, 디코더 첫 step의 입력을 나타내는 start 토큰 설정
        sos = torch.zeros(1, N, C)
        sos[:, :, -2] = 1

        # 타임스텝 T 동안 디코더 반복 실행
        for _ in range(T):
            # 디코더에 sos와 hidden state h_t를 전달하여 출력 계산
            y_t, h_t = self.decoder(sos, h_t)
            # 출력을 리스트에 저장
            y.append(y_t)

            # 다음 step의 입력을 현재 출력의 One-hot Encoding으로 설정
            sos = F.one_hot(y_t.argmax(dim=-1), num_classes=12).float().unsqueeze(0)

        # 리스트 y에 저장된 모든 y들을 dim=0 방향으로 합치기
        y = torch.cat(y, dim=0)

        return y


그 후 model과 optimizer를 정의한다.

model = Seq2Seq(dim_input=12, dim_recurrent=50, dim_output=12)
optimizer = optim.Adam(model.parameters())

Train

def plot_loss(losses):
    clear_output(wait=True)
    plt.figure(figsize=(10, 5))
    plt.plot(losses, label='Loss')
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.title('Loss & Epochs')
    plt.legend()
    plt.grid()
    plt.show()

우선 Epoch에 대한 Loss를 시각화 하기 위한 함수를 먼저 구현해준다.

이후에 아래처럼 본격적인 Train loop를 구현한다.



epochs = 10000
batch_size = 100

losses = []
loss_average_list = []

for epoch in range(epochs):
    _, x, label = generate_data(batch_size=batch_size)

    x = torch.tensor(x, dtype=torch.float32)
    label = torch.tensor(label, dtype=torch.long)

    optimizer.zero_grad()

    output = model(x)

    loss = nn.CrossEntropyLoss()(output.view(-1, 12), label.view(-1))
    losses.append(loss.item())

    loss.backward()

    optimizer.step()

    if epoch % batch_size == 0 and epoch > 0:
        loss_average = np.mean(losses)
        loss_average_list.append(loss_average)
        plot_loss(loss_average_list)
        print(f"Epoch {epoch}/{epochs}, Loss: {loss:.4f}")
print(f"Final loss average: {loss_average_list[-1]}")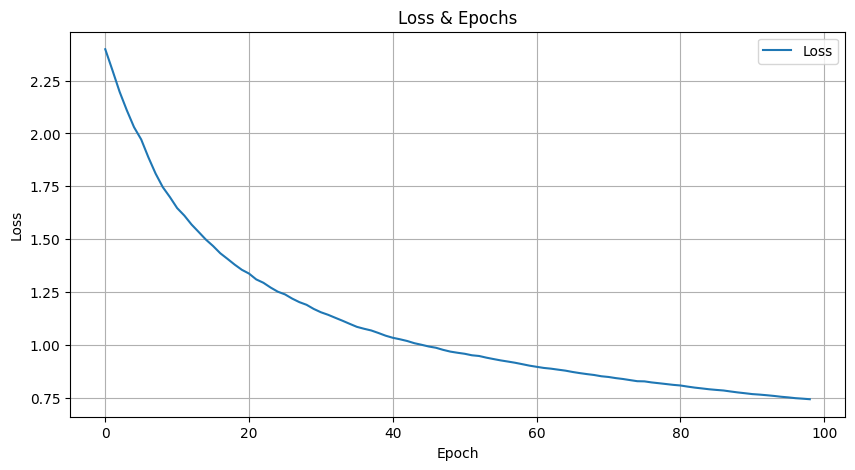

Epoch 9900/10000, Loss: 0.6189
Final loss average: 0.744258112165467

Test


length_total = defaultdict(int)
length_correct = defaultdict(int)

model.eval()
with torch.no_grad():
    for i in range(50000):
        if i % 5000 == 0:
            print(f"{i}번 test")
        if i == (50000-1):
            print(f"{i}번 test")
        # batch_size는 1로 지정
        sequence, x, label  = generate_data(1, 20, 1)

        x = torch.tensor(x, dtype=torch.float32)
        label = torch.tensor(label, dtype=torch.long)

        output = model(x)
        length_total[sequence.size] += 1
        if torch.all(output.argmax(dim=-1) == label):
            length_correct[sequence.size] += 1

테스트를 위한 loop를 구성한다. 이때 batch는 따로 만들어주지 않을 것이다.

0번 test
5000번 test
10000번 test
15000번 test
20000번 test
25000번 test
30000번 test
35000번 test
40000번 test
45000번 test
49999번 test


fig, ax = plt.subplots()
x, y = [], []
for i in range(1, 20):
    if length_total[i] > 0:
        x.append(i)
        y.append(length_correct[i] / length_total[i])
ax.plot(x, y);

Sequence의 길이에 따른 Accuracy값을 살펴볼 것이다. 결과는 아래와 같다.

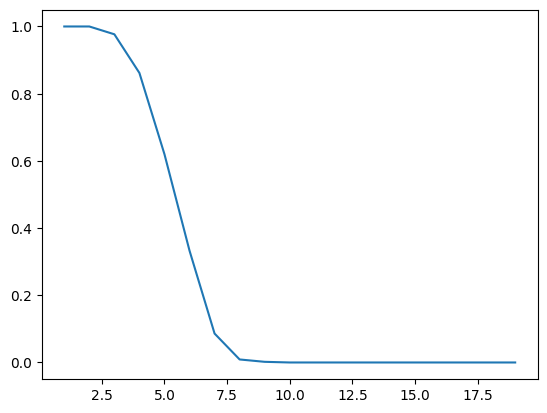무엇을 확인할 수 있을까? 바로 Sequence에 길이가 증가할수록 Accuracy가 감소한다는 것이다. 이러한 배경으로 인해 Transformer, Attention 모델이 탄생하게 된다.

profile
wh
열심히 배우는 중! 😌
이전 포스트

[딥러닝] Seq2Seq(Sequence-to-sequence)

다음 포스트

[딥러닝] GAN(Generative Adversarial Network)

0개의 댓글