신경망 I

퍼셉트론의 원리

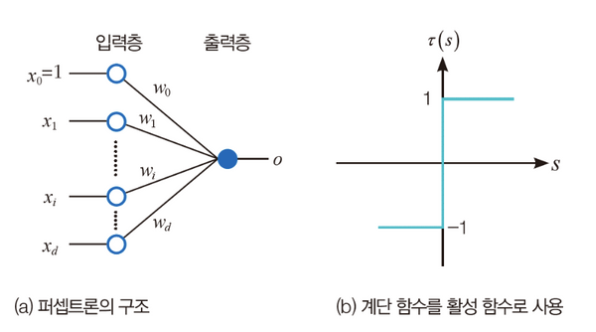
• 입력 값(입력 벡터) 과 가중치(가중치 벡터)의 일차 선형 결합으로 출력값이 결정
• 출력값을 활성함수의 input value로 사용
• 정확한 값을 계산하는 회귀(regression)가 아니며 threshold(임계값)을 기준으로 이진 분류를 하는 문제가 주어질 때, 활성함수로 계단함수를 활용할 수 있음
  • 특징 벡터를 1과 -1로만 변환하는 이진 분류기

행렬 표기

• 행렬을 표기할 때, 대문자로 표기
  • W와 X는 1 * d 행렬
  • 행렬 연산을 위해서는, (앞 행렬의 열의 수) 와 (뒤 행렬의 행의 수)를 일치시켜야 함
  • 따라서, 뒤에 등장하는 Matrix X를 전치행렬로 표기 (행 ↔ 열)
• 파이썬에서의 행렬 계산과정
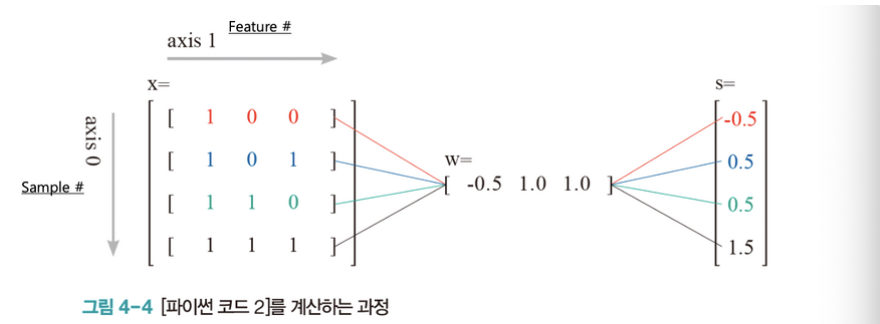
  • 별도의 전치행렬 변환과정이 필요없음. 간단한 array의 곱으로 표현 가능

신경망의 학습

• 실제 문제 상황
  • 데이터만 주어지므로 학습 알고리즘이 가중치를 직접 알아내야 함.
• 학습 원리

do initial W

While(true):
	w에 따른 손실함수 J(w) 계산

	# 손실함수 값의 허용오차 범위보다 작다면 break하고 가중치 벡터를 저장
	if (J(w) is satisfied) break

	# 손실함수 값이 허용오차 범위보다 크다면, 가중치를 수정(개선)
	delta(w)
	# 가중치 업데이트
	w = w + delta(w)

# 최종, 가중치를 저장
weigths = w

손실 함수 설계

• 손실 함수 J가 만족해야 할 조건

  

• 손실 함수값이 작아지는 방향으로 학습을 추가 진행 ⇒ 경사 하강법을 이용

  • 경사 하강법에 따른 미분값을 사용하여 기울기 값을 구함
    • 기울기가 음수이면, w를 증가시킬 수록(오른쪽 이동) 손실함수 값이 감소
    • 기울기가 양수이면, w를 감소시킬 수록(왼쪽 이동) 손실함수 값이 감소

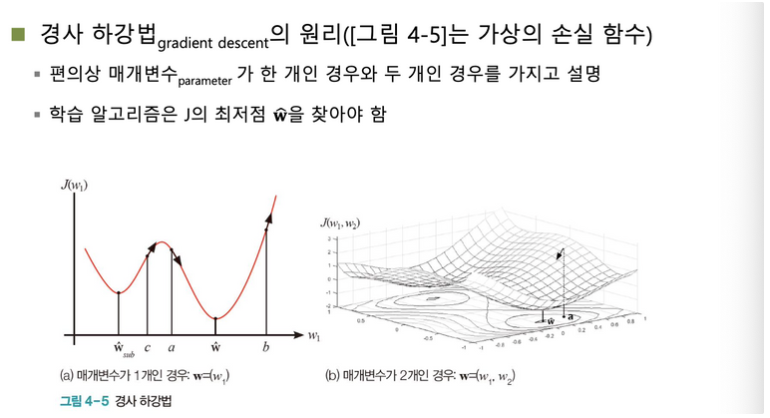
• ML은 어느 지점이 Local Minimum인지 Global Minimum인지 알 수 없음
  • Learning rate을 작게 설정한 경우, Local Minimum에 갇혀서 최적의 값을 찾지 못할 수도 있음
  • Learning rate을 크게 설정한 경우, 이동이 커서 Minimum을 찾지 못할 수도 있거나 방향 전환이 잦을 수 있음

학습 알고리즘 설계

• 실제 데이터에 적합하는 함수를 알지 못함.
  • 따라서, 손실함수에서는 실제 값과 계산된 예측값 사이의 차이를 손실함수에 반영