[Divide and Conquer] Merge Sort 구현하기 - C언어

안녕하세요

예전에 파이썬으로 Merge Sort 알고리즘을 구현해본 적이 있었습니다.

이번에는 C언어로 Merge Sort를 한 번 구현해 볼텐데요~
추가적으로 시간 복잡도와 공간 복잡도에 대해서도 분석해봅시다..!

---

Merge Sort 알고리즘이란

먼저 Merge Sort에 대해서 간단하게 알려드리자면,
합병 정렬이라고도 불리는 Merge Sort는 입력이 2개의 부분문제로 분할되고, 부분문제의 크기가 $1\over2$로 감소하는 분할 정복 알고리즘입니다.

즉, $n$개의 숫자들을 $n\over2$개씩 $2$개의 부분문제로 분할하고, 각각의 부분문제를 순환적으로 합병 정렬한 후, $2$개의 정렬된 부분을 합병하여 정렬하게 되는 것이죠.

이 알고리즘을 처음 접하신 분들이라면, 이 설명만으로는 이해가 어려우실 겁니다😂 이 분할정복 알고리즘은 문제 해결 방식의 대표적인 알고리즘 중 하나이기 때문에, 관련 자료도 많고 잘 정리된 설명들도 많으니 한 번 찾아보시는 걸 추천합니다.

파이썬에서 구현했던 걸 조금 더 보완해서 이번에는 C언어로 구현해 보았습니다!

코드 및 주석

#include <stdio.h>
#define MAX 8 // 배열의 길이

// 배열을 순서대로 출력하는 함수
void printArr(int list[]) {
    for (int i = 0; i < MAX; i++) {
        printf("%d | ", list[i]);
    }
    printf("\n");
}

// 기존의 배열에 정렬된 배열을 덮어씌우는 함수
void inputArr(int list1[], int list2[], int start, int end) {
    int k = 0; // mergeSortArr의 시작 인덱스를 맞추기 위한 변수
    for (int i = start; i <= end; i++){
        list1[i] = list2[k++];
    }
}

// conquer 함수
void merge(int list[], int first, int mid, int last) {
    int mergeSortArr[1000]; // 정렬된 배열을 저장하는 변수
    int i = first; // 왼쪽 배열의 첫번째 인덱스
    int j = mid + 1; // 오른쪽 배열의 첫번째 인덱스
    int k = 0; // 정렬된 배열의 인덱스

    // 두 배열의 인덱스가 각각 마지막 인덱스가 될 때까지 반복한다.
    while (i <= mid && j <= last) {
        
        // 만약 왼쪽 요소가 오른쪽 요소보다 작다면
        if (list[i] <= list[j]) {
            // 새로운(정렬된) 배열에 현재의 왼쪽 요소를 저장한다.
            mergeSortArr[k] = list[i];
            i++; // 왼쪽 배열의 요소를 하나 저장했기 때문에 인덱스를 업데이트 해준다.
            k++; // 새로운(정렬된) 배열의 인덱스를 업데이트 해준다.
        }
        // 만약 왼쪽 요소보다 오른쪽 요소가 작다면
        else {
            // 새로운 배열에 현재의 오른쪽 요소를 저장한다.
            mergeSortArr[k] = list[j];
            j++; // 오른쪽 배열의 요소를 하나 저장했기 때문에 인덱스를 업데이트 해준다.
            k++; // 새로운 배열의 인덱스를 업데이트 해준다.
        }
    }

    // 왼쪽 배열의 요소가 남아있다면 순서대로 새로운 배열에 저장한다.
    while (i <= mid) {
        mergeSortArr[k++] = list[i++];
    }

    // 오른쪽 배열의 요소가 남아있다면 순서대로 새로운 배열에 저장한다.
    while (j <= last) {
        mergeSortArr[k++] = list[j++];
    }

    // 정렬된 mergeSortArr배열을 원래의 배열 list에 복사하는 함수를 호출한다.
    inputArr(list, mergeSortArr, first, last);
}

// divide 함수
// 배열과 배열의 첫번째 인덱스, 마지막 인덱스를 파라미터로 받는다.
void mergeSort(int list[], int first, int last) {
    
    // 첫번째 인덱스가 마지막 인덱스보다 작다면 재귀 함수를 실행한다.
    // 같거나 크면 재귀 함수를 호출하지 않는다.
    if (first < last) {
        // mid 에는 현재 배열의 중간지점 인덱스 값을 저장한다.
        int mid = (first + last) / 2;

        // 중간 인덱스를 기준으로 분할한 배열의 왼쪽을 가지고
        // 함수를 재귀 호출한다.
        // 최초 실행 시 배열의 첫번째 요소만 남을 때까지 분할한다.
        mergeSort(list, first, mid);

        // 중간 인덱스를 기준으로 분할한 배열의 오른쪽을 가지고
        // 함수를 재귀 호출한다.
        mergeSort(list, mid + 1, last);

        // 분할된 왼쪽 배열과 오른쪽 배열을 merge 함수를 통해 정렬시킨다.
        merge(list, first, mid, last);
    } else {
        // 재귀함수 조건에 만족하지 못한다면, 함수를 종료한다.
        return;
    }
}

int main(int args, char* argv[]) {
    
    // 배열 생성 및 정의
    int arr[] = {37, 10, 22, 30, 35, 13, 25, 24};

    // 기존 배열 출력
    printArr(arr);

    // 생성한 배열, 첫번째 인덱스와 마지막 인덱스를 파라미터로 보낸다.
    mergeSort(arr, 0, MAX – 1); // mergeSort 함수 호출

    // 정렬된 함수를 출력한다.
    printArr(arr);

    return 0;
}

실행 화면

배열 arr = { 37, 10, 22, 30, 35, 13, 25, 24 }을 정렬해 보도록 하겠습니다.

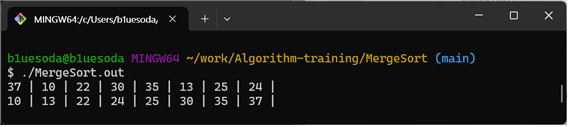
정렬이 잘 되는 모습을 볼 수 있습니다👍

복잡성

시간 복잡성

Merge Sort에서 재귀 함수를 거칠 때에는 배열이 반으로 나뉘므로 $log{n}$ 의 시간 복잡도를 가집니다.
그리고 각 수준에서 병합 프로세스는 만큼의 시간 복잡도가 걸리므로, 총 시간 복잡성은 $O(nlog{n})$이 됩니다.

여기서 알 수 있었던 점은 배열이 이미 정렬되어 있든, 안되어 있든 항상 동일한 수준의 시간 복잡성을 가진다는 것입니다!😲

공간 복잡성

그렇다면 공간 복잡도는 어떨까요?
제가 작성한 코드 중에 정렬된 배열을 보관하기 위해 임시 배열 MergeSortArr[]을 생성하는 과정이 있습니다.
이 임시 배열은 입력 배열의 크기에 비례하죠?
하지만 전체 공간은 입력 크기에 따라 기하급수적으로 증가하지 않기 때문에 공간 복잡도가 $O(n)$이 됩니다.

시간 복잡도를 분석했을 때와 마찬가지로, 배열이 이미 정렬되어 있든 안되어 있든 임시 배열을 위해 필요한 추가 공간은 동일하다는 것을 알 수 있습니다! 😲

---

오늘은 Merge Sort 알고리즘을 C언어로 구현해보고, 어느 정도의 시간 복잡성과 공간 복잡성을 가지는지 한 번 분석해 보았는데요
결론적으로 일관된 시간 복잡성과 공간 복잡성 덕분에 대규모 데이터 세트를 정리하는 데 성능이 효율적일 것 같다는 생각이 들었습니다👻

그럼 다음 포스트로 찾아뵙겠습니다. 읽어주셔서 감사합니다 :)

---

📚Reference
Merge Sort – Data Structure and Algorithms Tutorials