안녕하세요👻
오늘은 Selection 알고리즘을 한 번 구현해보겠습니다.

---

문제

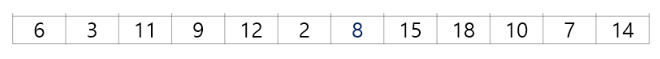
• 아래의 pseudo code를 참조하여 selection 알고리즘을 구현하시오.
• 위의 주어진 입력값들중 7번째로 작은 값을 찾으시오.
• 1~200,000 사이의 랜덤한 100,000개의 값을 입력받고
• 100,000개중 30,000번째 작은 값을 찾으시오.

psudo code

---

풀이

main.c

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "selection.h"
#define MAX 100000

int main() {
    srand(time(NULL)); // 난수 생성기 초기화

    int arr1[12] = {6, 3, 11, 9, 12, 2, 8, 15, 18, 10, 7, 14}; // 임의의 배열
    int small_arr1 = 7; // arr1에서 n번째로 작은 값
    
    int arr2[MAX]; // 랜덤한 값 입력 받을 배열
    int small_arr2 = 30000; // arr2에서 n번째로 작은 값
    // arr2에 랜덤한 값 입력 받기
    for (int i = 0; i < MAX; i++) {
        arr2[i] = rand() % 200000 + 1;
    }

    int n = sizeof(arr1) / sizeof(arr1[0]); // pivot을 기준으로 배열을 나눌 때 사용할 배열의 크기
    printArr(arr1, n); // arr1 출력
    printf("arr1에서 %d번째로 작은 값: %d\n\n", small_arr1, Selection(arr1, 0, 11, small_arr1)); // arr1에서 n번째로 작은 값 출력

    clock_t start, end; // 시간 측정을 위한 변수 
    start = clock(); // 시간 측정 시작
    printf("arr2에서 %d번째로 작은 값: %d\n", small_arr2, Selection(arr2, 0, MAX - 1, small_arr2)); // arr2에서 n번째로 작은 값 출력
    end = clock(); // 시간 측정 종료
    printf("Time: %f\n", (double)(end - start) / CLOCKS_PER_SEC); // 시간 출력

    return 0;
}

selection.h

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

// 배열 출력
void printArr(int arr[], int n) {
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("\n");
}

// 배열 내 두 원소의 위치를 바꾸는 함수
void swap(int *a, int *b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 피봇을 기준으로 배열을 두 부분으로 나누는 함수
int partition(int arr[], int left, int right) {
    int pivotindex = left + rand() % (right - left + 1); // 랜덤한 pivot 선택
    int pivot = arr[pivotindex];
    swap(&arr[pivotindex], &arr[left]); // pivot을 배열의 시작점으로 이동
    int i = left + 1;
    for(int j = left + 1; j <= right; j++) {
        if(arr[j] < pivot) {
            swap(&arr[j], &arr[i]);
            i++;
        }
    }
    swap(&arr[left], &arr[i - 1]); // pivot을 최종 위치로 이동
    return i - 1; // pivot의 최종 위치 반환
}

// 선택 알고리즘
int Selection(int arr[], int left, int right, int k) {
    if (left == right) {
        return arr[left]; // 배열에 원소가 하나만 있을 경우
    }
    int p = partition(arr, left, right); // 피봇을 기준으로 배열을 나눔
    int S = (p - 1) - left + 1; // 피봇의 위치를 기준으로 왼쪽 배열의 크기
    if (k <= S) {
        return Selection(arr, left, p - 1, k); // 왼쪽 배열에서 k번째로 작은 원소를 찾음
    }
    else if (k == S + 1) {
        return arr[p]; // 피봇이 k번째로 작은 원소인 경우
    }
    else {
        return Selection(arr, p + 1, right, k - S - 1); // 오른쪽 배열에서 k번째로 작은 원소를 찾음
    }
}

---

실행 결과

주어진 배열 arr1 에서 7번째로 작은 값인 10이 잘 출력이 되었고, 1~200,000 사이의 랜덤한 값 100,000개를 입력 받은 배열 arr2에서 30,000번째 작은 값으로 9934가 출력되었다.

bad 분할 결과

good 분할 결과

프로그램을 반복적으로 실행했을 때, 걸린 시간이 0.002 혹은 0.001로 측정되었다. 이는 bad 분할일 때와 good 분할일 때의 결과가 다르다는 것을 알 수 있다!

---

결론

오늘은 Selection 알고리즘에 대해 공부해보았습니다😎

Selection 알고리즘은 분할 정복 알고리즘이기도 하지만 피봇을 랜덤하게 정하기 때문에 랜덤 알고리즘이기도 합니다.
이 분할 정복 알고리즘에서는 배열이나 리스트를 두 부분으로 나누고, 각 부분을 재귀적으로 정렬하거나 처리합니다.
이 때, 나누어진 두 부분의 크기가 비슷할수록(good 분할), 알고리즘의 효율성이 높아진다. 반대로, 한 쪽이 다른 쪽보다 훨씬 크면(bad 분할), 알고리즘의 수행 시간이 증가하게 됩니다.
프로그램 실행 결과를 통해, bad 분할이 되었을 때 시간이 good 분할이 되었을 때보다 시간이 2배 걸린 것을 확인할 수 있었습니다.
물론 이러한 시간 차이는 매우 작기 때문에 실제 애플리케이션에서는 큰 영향을 미치지 않을 수 있지만,
분할 정복 알고리즘의 성능을 이해하는 데 확실히 도움이 되었습니다👻

---

📚Reference
Selection Sort

🚩Source Code
Algorithm-training