[Contents]

1. Numpy
2. Handling shape
3. indexing & slicing
4. creation functions
5. operation functions
6. array operations
7. comparisons
8. boolean & fancy index
9. numpy data i/0
10. 벡터
11. 벡터의 노름 구해보기
12. 행렬

Numpy

• numpy는 파이썬으로 진행되는 모든 데이터 분석과 인공지능 학습에 있어 가장 필수적으로 이해해야 하는 도구이다
• Numpy는 Numerical Python의 약자로 일반적으로 과학계산에서 많이 사용하는 선형대수의 계산식을 파이썬으로 구현할 수 있는도록 도와주는 라이브러리 이다
• Numpy는 numpy 자체로도 많이 사용되지만 이후에 사용되는 SciPy나 Pandas의 base객체로도 사용되며 numpy에서 사용된느 다양한 코드 표현법을 pytorch와 tensorflow에 사용하는 경우가 많아 numpy의 활용법은 반드시 알아둘 필요가 있다

• 파이썬의 고성능 과학 계산용 패키지

• Matrix와 Vector와 같은 Array 연산의 사실상의 표준

• 일반 list에 비해 빠르고, 메모리 효율적

• 반복문 없이 데이터 배열에 대한 처리를 지원함

• 선형대수와 관련된 다양한 기능을 제공함

• C, C++, 포트란 등의 언어와 통합 가능

• array creation

  • numpy는 np.array 함수를 활용 배열을 생성함
  • numpy는 하나의 데이터 type 만 배열에 넣을 수 있음
  • list와 가장 큰 차이점 - > dynamic typing not supported
  • C의 Array를 사용하여 배열을 생성함

test_array = np.array(["1",4.0,5,6], float)
print(test_array) # array([1., 4., 5., 8.])
print(type(test_array[0]) # numpy.float64

• numpy array vs python list 구조

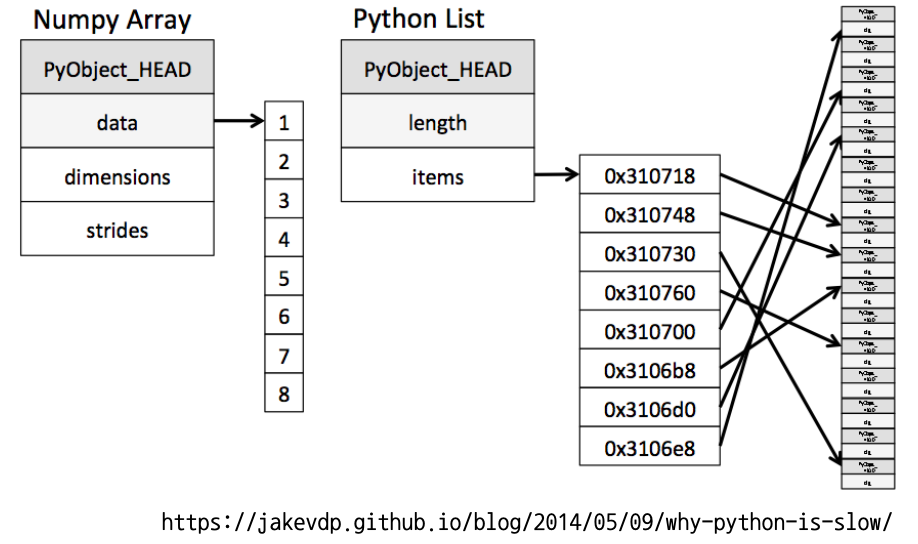
• python list

  • python list는 -5 ~ 256의 값이 메모리 어딘가 static한 공간에 있다
  • 그렇기 때문에 -5 ~ 256 값들 중 python list에 할당한다면 값들 자체를 list에 넣는게 아니라 값들의 주소값을 리스트에 차례대로 저장한다
  • 그렇기 때문에 데이터의 값을 확보하기 위해선 (2차원이라면) 2단계를 거처 데이터의 값을 확인해야한다

• numpy array

  • numpy array는 차례대로 데이터가 메모리에 할당되기 때문에 연산이 굉장히 빨라진다
  • 메모리의 크기가 일정하기 때문에 데이터를 저장하는 공간을 잡는 방법도 효율적이다

import numpy as np
a = [1, 2, 3, 4, 5]
b = [5, 4, 3, 2, 1]
a[0] is b[-1] # True

a = np.array(a)
b = np.array(b)
a[0] is b[-1] # False

• numpy array 용어

  • shape : numpy array의 dimension 구성을 반환함
    • array의 크기, 형태 등에 대한 정보
  • dtype : numpy array의 data type을 반환함
    • ndarray의 single element가 가지는 data type
    • 각 element가 차지한느 memory의 크기가 결정됨
    • array는 list와 다르게 dynamic supporting을 지원하지 않기 때문에 한가지 data type만 ndarray에 저장 가능하다
  • ndim : number of dimensions
  • size : data의 개수

• array shape

  • array의 Rank에 따라 불리는 이름이 있음

Rank	Name	Exampe
0	scalar	7
1	vector	[10, 10]
2	matrix	[[10, 10], [15,15]]
3	3-tensor	[[[1,5,9], [2,6,10]], [[3,5,11],[4,8,12]]]
n	n-tensor

• array shape (3rd order tensor)
  

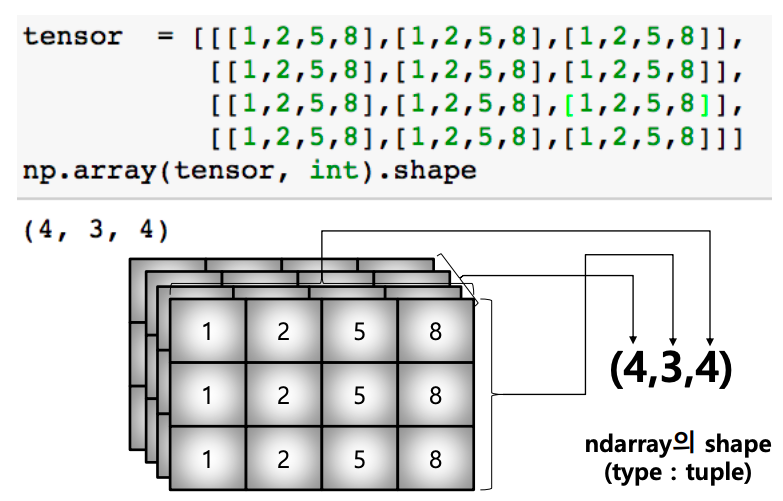
• array nbytes

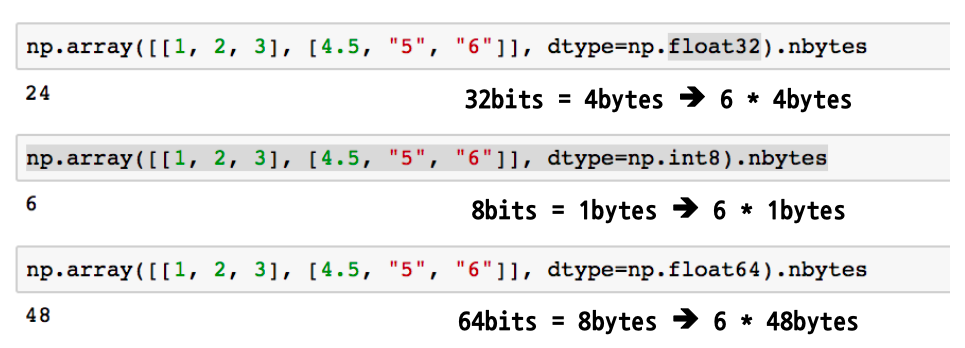
  • nbytes : ndarray object의 메모리 크기를 반환함
    

Handling Shape

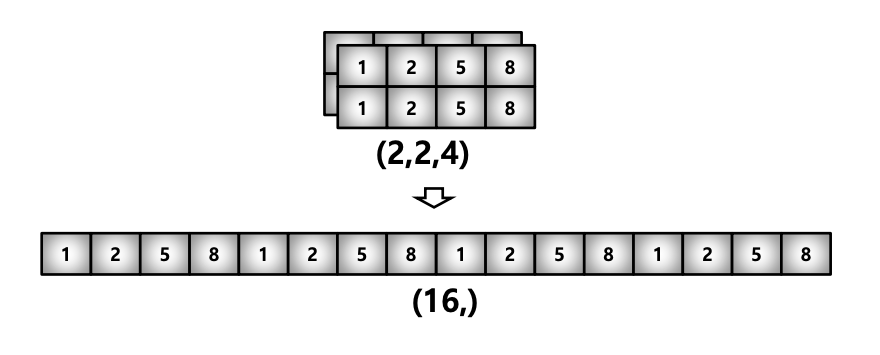
• reshape : Array의 shape의 크기를 변경함, element의 갯수는 동일

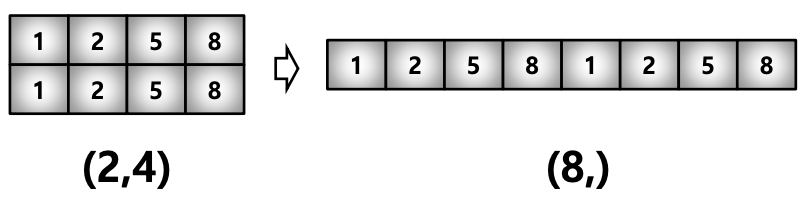
test_matrix = [[1,2,3,4], [1,2,5,8]]
np.array(test_matrix).shape # (2,4)

np.array(test_matrix).reshape(8,)
# array([1,2,3,4,1,2,5,8])

np.array(test_matrix).reshape(2,4).shape # (2,4)
np.array(test_matrix).reshape(-1, 2).shape # (4,2). -1 : size를 기반으로 row 개수 선정 

np.array(test_matrix).reshape(2,2,2) # [[[1,2],[3,4]],[[1,2],[5,8]]]
np.array(test_matrix).(1,-1,2).shape # (1,4,2)

• flatten : 다차원 array를 1차원 array로 변환
  

indexing & slicing

• indexing for numpy array
  • lists와 달리 이차원 배열에서 [0,0] 표기법을 제공함
  • matrix일 경우 앞은 row 뒤는 column을 의미함

a = np.array([[1, 2, 3], [4.5, 5, 6]], int)
print(a) # array([[1,2,3],[4,5,6]])
print(a[0,0]) # 1)Two dimensional array representation
print(a[0][0]) # 2)Two dimensional array representation 
a[0,0] = 12 # Matrix 0,0 에 12 할당
print(a) # array([[12,2,3],[4,5,6]])
a[0][0] = 5 # Matrix 0,0 에 12 할당
print(a) # array([[5,2,3],[4,5,6]])

• slicing for numpy array
  • list와 달리 행과 열 부분을 나눠서 slicing이 가능함
  • matrix의 부분 집합을 추출할 때 유용함

import numpy as np
a = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]], int)
print(a[:,2:]) # 전체 Row의 2열 이상 # [[3,4,5],[8,9,10]]
print(a[1,1:3]) # 1 Row의 1열 ~ 2열 # [7,8]
print(a[1:3]) # 1 Row ~ 2Row의 전체 # [[6,7,8,9,10]]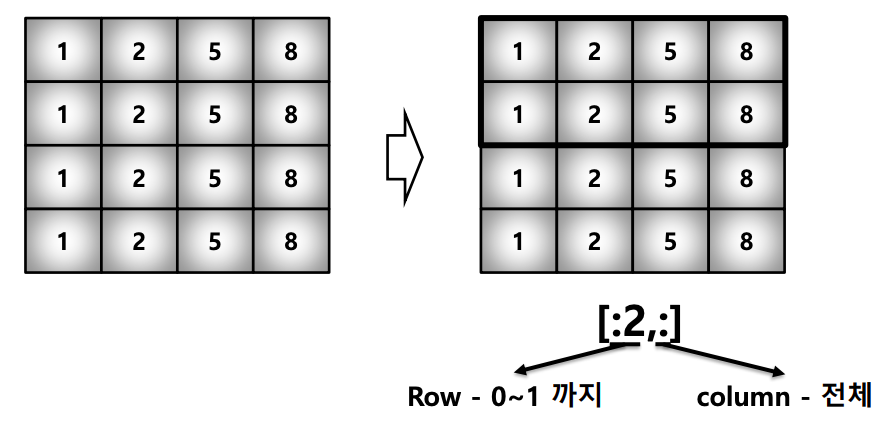

• arr[start:end:step, start:end:step]

creation function

• arange
  • array의 법위를 지정하여, 값의 list를 생성하는 명령어

import numpy as np
print(np.arange(10)) # range : list의 range와 같은 효과, integer로 0부터 29까지 배열 추출 # [0 1 2 3 4 5 6 7 8 9]
print(np.arange(0,5,0.5)) # floating point 도 표시가능함. np.arange(시작, 끝, step) # [0.  0.5 1.  1.5 2.  2.5 3.  3.5 4.  4.5]
print(np.arange(15).reshape(5,-1)) # [[0,1,2],[3,4,5],[6,7,8],[9,10,11],[12,13,14]]

• zeros : 0 으로 가득찬 ndarray 생성

np.zeros(shape = (10,), dtypes = np.int8) # 10 - zero vector 생성
# array([0,0,0,0,0,0,0,0,0,0], dtype = int8)

np.zeros((2,5)) # 2 by 5 - zeros matrix 생성

• ones : 1로 가득찬 ndarray 생성
• empty : shape만 주어지고 비어있는 ndarray생성 (memory initialization 이 되지 않음)
  • 빈 공간만 잡아주므로 빈공간이 이전에 다른 프로그램이 썻던 공간일 경우 그 값이 그대로 반환 된다
• something_like : 기존 ndarray의 shape 크기 만큼 1,0 또는 empty array를 반환

import numpy as np
test_matrix = np.arange(9).reshape(3,3)
np.ones_like(test_matrix) # [[1,1,1],[1,1,1],[1,1,1]]

• identity : 단위 행렬(i 행렬)을 생성함 (대각행렬)

import numpy as np
np.identity(n=3, dtype=np.int8)
# [[1,0,0]]
#  [0,1,0]]
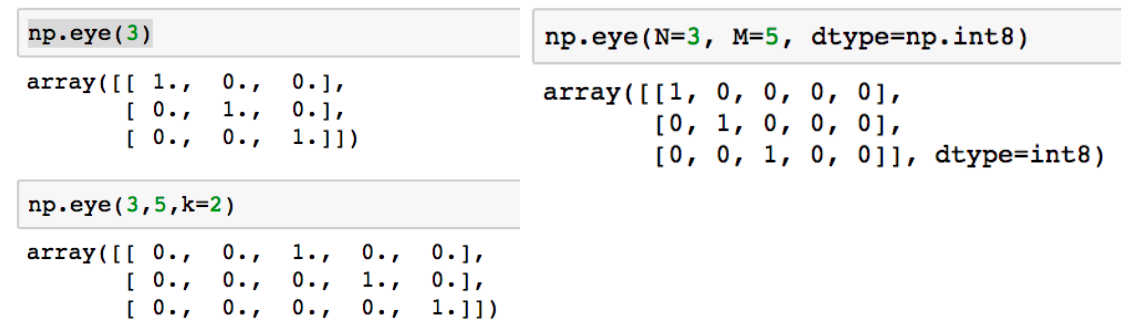
#  [0,0,1]]

• eye : 대각선인 1인 행렬, k값의 시작 index의 변경이 가능

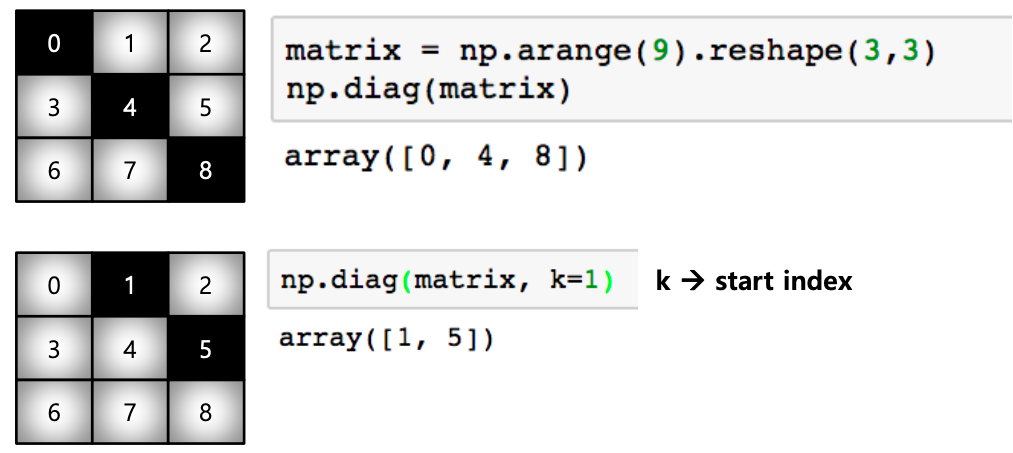
• diag : 대각 행렬의 값을 추출함

• random sampling
  • 데이터 분포에 따른 sampling으로 array를 새엉

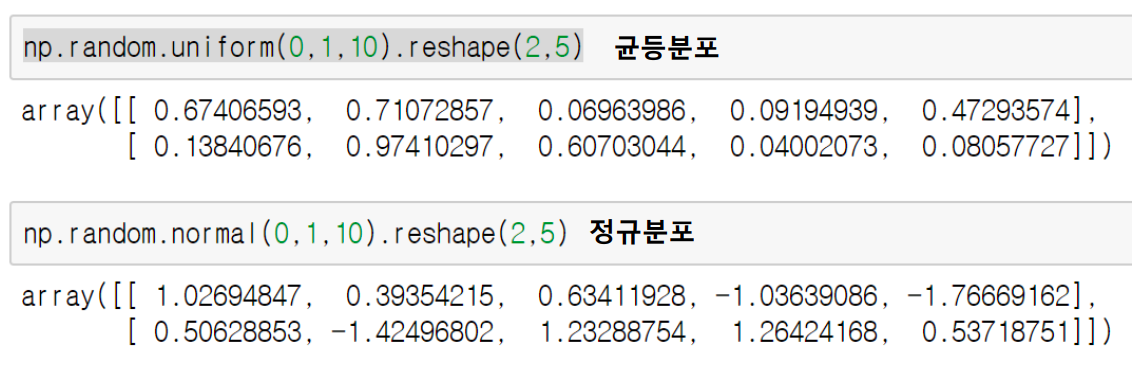
operation functions

• ndarray element들 간의 여러가지 연산을 할 때 활용하는 함수들
• 연산을 어떻게 지원을 해주는지 알아야 한다
  • axis 개념을 알아야 한다

• sum : ndarray의 element들 간의 합을 구함, list의 sum 기능과 동일

test_array = np.arange(1,11)
test_array.sum(dtype = np.float) # 55.0

• axis : 모든 operation function을 실행할 때 기준이 되는 dimension 축

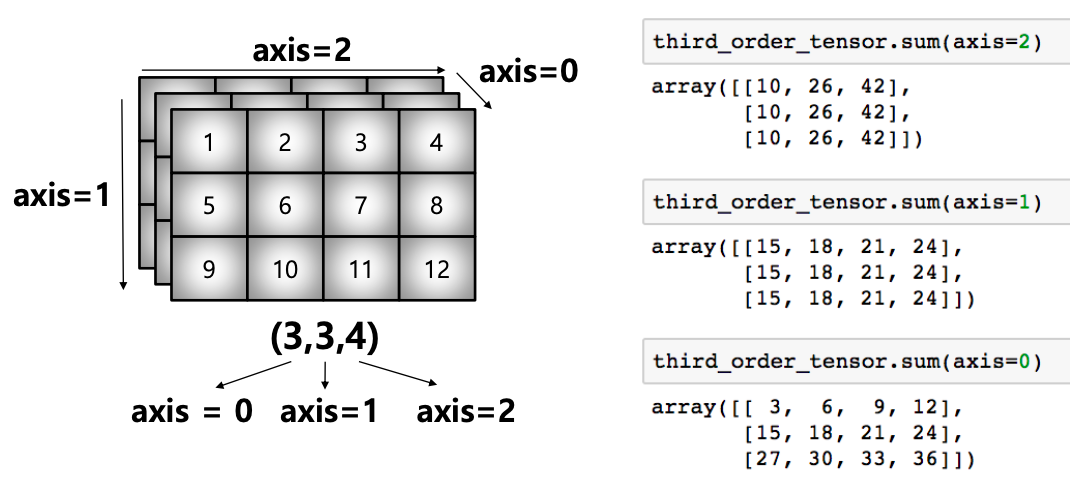
• mean & std : ndarray의 element들 간의 평균 또는 표준편차를 반환
• 그 외에도 다양한 수학 연산자를 제공함 (np.something 호출)
• concatenate : numpy array 를 합치는 (붙이는) 함수

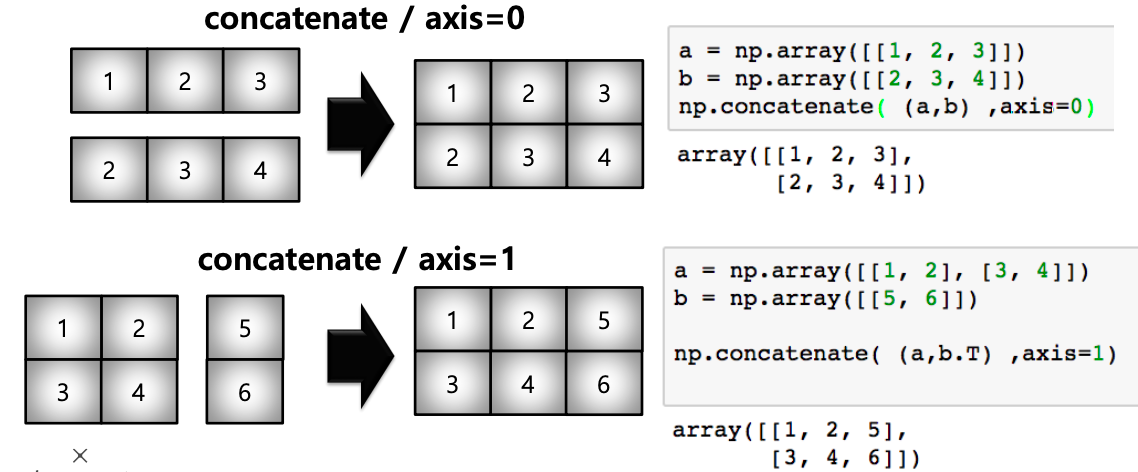
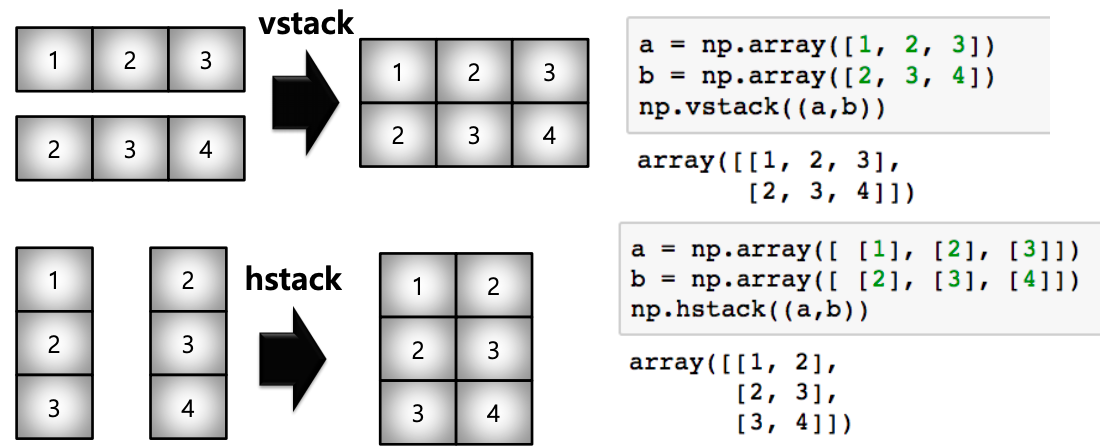
import numpy as np
a = np.array([[1,2,],[3,4]])
b = np.array([5,6])

b = b[np.newaxis, :] # 값은 그대로면서 축이 하나 추가 or b = b.reshape(-1,2) 
print(b) # [[5,6]]
np.concatenate((a,b.T), axis=1) # [[1,2,5],[3,4,6]]

or 

import numpy as np
a = np.array([[1,2,],[3,4]])
b = np.array([5,6])

b = b[: ,np.newaxis] # 값은 그대로면서 축이 하나 추가 or b = b.reshape(2,-1)
print(b) # [[5],[6]]
np.concatenate((a,b), axis=1) # [[1,2,5],[3,4,6]]

array operations

• numpy 는 array간의 기본적인 사칙 연산을 지원함
• element-wise operations
  • array간 shape이 같을 때 일어나는 연산

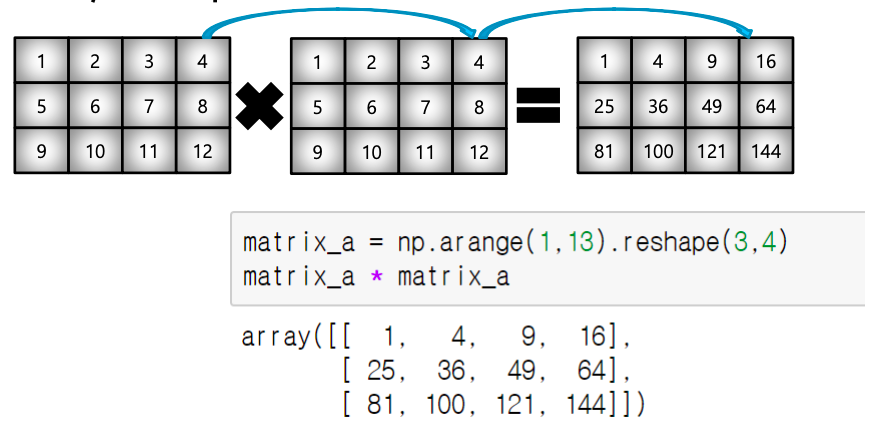
• dot product
  • matrix의 기본 연산, dot 함수 사용

o

• transpose
  • transpose 또는 T attribute 사용

test_a = np.arange(1,7).reshape(2,3) # [[1,2,3],[4,5,6]]
test_a.transpose() # [[1,4],[2,5],[3,5]]

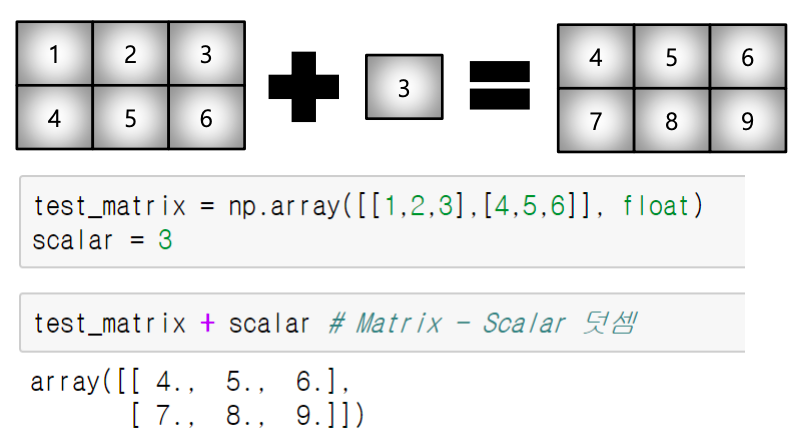
test_a.T.dot(test_a) # matrix간 곱셈

• broadcasting
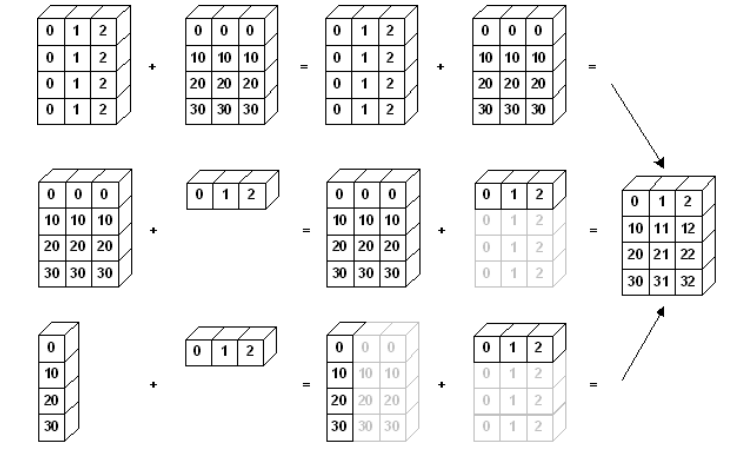
  • shape이 다른 배열 간 연산을 지원하는 기능

• broadcasting cont.
  • scalar - vector 외에도 vector - matrix 간의 연산도 지원

• numpy performance # 1
  • timeit : jupyter 환경에서 코드의 퍼포먼스를 체크하는 함수
  • 일반적으로 속도는 아래 순
    • for loop < list comprehension < numpy
  • 100,000,000 번의 loop이 돌 때, 약 4배 이상의 성능 차이를 보임
  • Numpy는 C로 구현되어 있어, 성능을 확보하는 대신 파이썬의 가장 큰 특징인 dynamic typing을 포기함
  • 대용량 계산에서는 가장 흔히 사용됨
  • concatenate 처럼 계산이 아닌, 할당에서는 연산 속도의 이점이 없음

import numpy as np
def sclar_vector_product(scalar, vector):
    result = []
    for value in vector:
        result.append(scalar * value)
    return result

iternation_max = 100000000

vector = list(range(iternation_max))
scalar = 2

%timeit sclar_vector_product(scalar, vector) # for loop을 이용한 성능
%timeit [scalar * value for value in range(iternation_max)]
# list comprehension을 이용한 성능
%timeit np.arange(iternation_max) * scalar # numpy를 이용한 성능

comparisons

• All & Any
  • array의 데이터 전부(and) 또는 일부(or)가 조건에 만족 여부 반환

a = np.arange(10)
print(a) # array([0,1,2,3,4,5,6,7,8,9])

np.any(a>5) # True
np.any(a<0) # False # any -> 하나라도 조건에 만족한다면 True

np.all(a>5) # False
np.all(a<10) # True # all -> 모두가 조건에 만족한다면 True

• comparison operation # 1
  • numpy 는 배열의 크기가 동일 할 때 element간 비교의 결과를 boolean type 으로 반환

test_a = np.array([1,3,0], float)
test_b = np.array([5,2,1], float)
test_a > test_b # array([False, True, False], dtype=bool)
(test_a > test_b).any() # True 

a = np.array([1,3,0], float)
np.logical_and(a>0, a<3) # and 조건의 condition
# array([True, False, False], dtype=bool)

b = np.array([True,False,True], bool)
np.logical_not(b) # Not 조건의 condition
# array([False, True, False], dtype = bool) 

c = no.array([False, True, False], bool)
np.logical_or(b,c) # or 조건의 condition
# array([True, True, True], dtype = bool)

# np.where
import numpy as np
a = np.arange(5)
np.where(a>2, 'Correct', 'Wrong') # where(condition, True, False)
# array(['Wrong', 'Wrong', 'Wrong', 'Correct', 'Correct'], dtype='<U7')

a = np.arange(10) 
np.where(a>5) # array([6,7,8,9]) # index 값 반환

a = np.array([1, np.NaN, np.Inf], float) # Not a Number
np.isnan(a) # array([False, True, False], dtype = bool)

np.isfinite(a) # is finite number
array([True, False, False], type=bool)

• argmax & argmin

#array 내 최대값 또는 최소값의 index를 반환함
a = np.array([1,2,3,4,5,6,78,23,3])
np.argmax(a) # 5
np.argmin(a) # 0

#axis 기반의 반환
a = np.array([[1,2,4,7],[9,88,6,45],[9,76,3,4]])
np.argmax(a, axis= 1) # array([3,1,1])
np.argmax(a, axis=0) # array([0,0,2,2])

boolean & fancy index

• boolean index
  • 특정 조건에 따른 값을 배열 형태로 추출
  • comparison opeation 함수들도 모두 사용가능
  • 조건이 True인 index 값들을 반환
  • 원개 array 와 boolean index의 shape이 같아야 한다
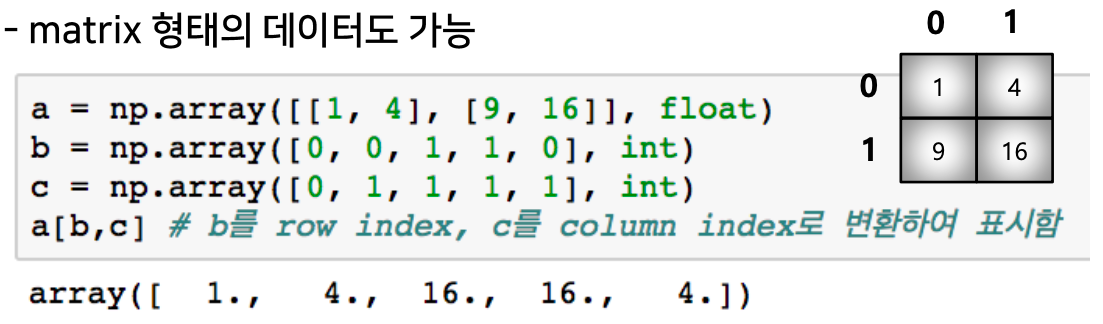
• fancy index
  • numpy는 array를 index value로 사용해서 값 추출

• fancy index (cont.)

numpy data i/o

• leadtxt & savetxt
  • text type 의 데이터를 읽고, 저장하는 기능

a = np.loadtxt('./populations.txt') # 파일 호출

a_int = a.astype(int)
a_int[:3] # int type 변환

np.savetxt('int_data.csv', a_int, delimiter=',') # int_data.csv 로저장

벡터

• 벡터의 기본 개념과 연산, 노름에 대해 소개
• 두 벡터 사이의 거리와 각도, 그리고 내적에 대해 설명
• 벡터는, 딥러닝에서 매우 중요한 선형대수학의 기본 단위가 되고, 앞으로 배울 numpy에서도 굉장히 많이 사용되는 연산이기 때문에 확실히 알아야 함!!
• 벡터간의 연산을 단순히 숫자 계산으로 끝내기보단, 공간에서 어떤 의미를 가지는지를 이해하는 것이 중요!
• 노름이나 내적 같은 개념 또한, 그 자체로 가지는 기하학적인 성질과 이것이 실제 머신러닝에서 어떻게 사용되는지를 생각!!

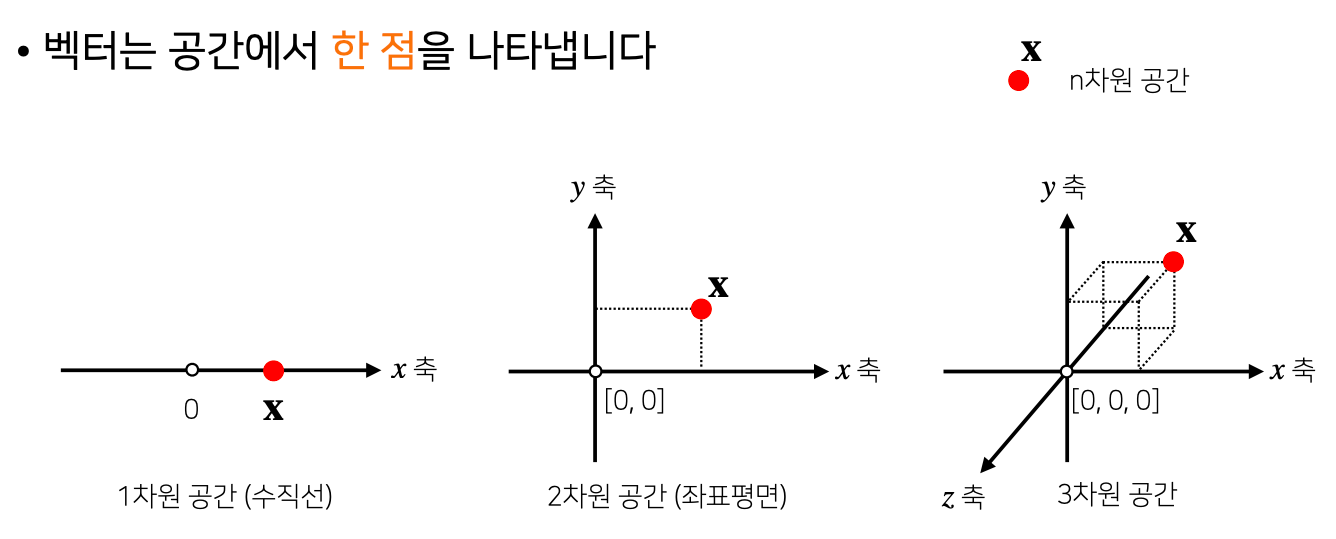
• 벡터는 숫자를 원소로 가지는 리스트(list) 또는 배열(array) 이다
  • 새로로 나열 = 열 벡터
  • 가로로 나열 = 행 벡터

• 각각의 벡터마다 차원의 갯수를 정의를 한다

  • 벡터의 차원 = 벡터에 있는 숫자들의 갯수

• 벡터 (cont.)

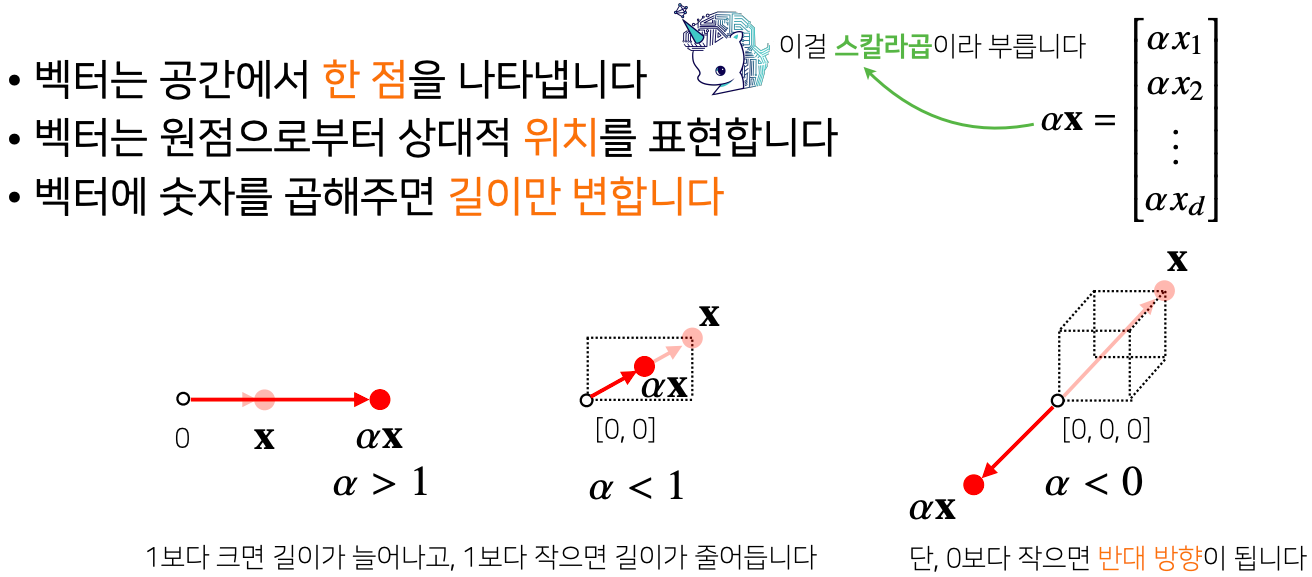
• 어떤 한 벡터가 있을 때 그 벡터에 scalar 또는 숫자를 곱해주게 되면 방향은 그대로고 벡터의 길이만 변형되는데 이 연산을 스칼라곱 이라고 부른다
• 스칼라곱의 의미 - 주어진 벡터의 길이를 변형 시키는 것으로써 만약의 숫자의 크기가 1보다 크면 원래 벡터의 길이를 더 길게 변화를 시키는 것이고 만약 1보다 작다면 원래 벡터의 길이를 1보다 작은 크기로 줄인다
• 만약에 곱해주는 실수의 값이 0 보다 작다면 이 때는 벡터가 같은 방향으로 가지 않고 반대 방향으로 가게 된다
• 정리 - 원점에서 그 벡터를 표현하는 화살표를 스칼라곱을 통해서 길이를 변형 시켜주는 연산

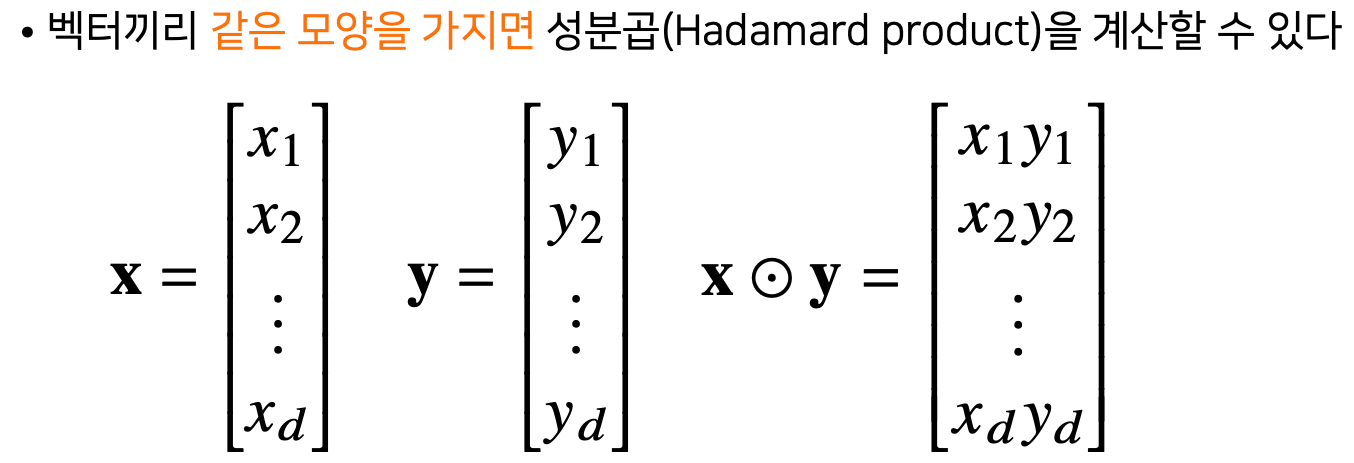
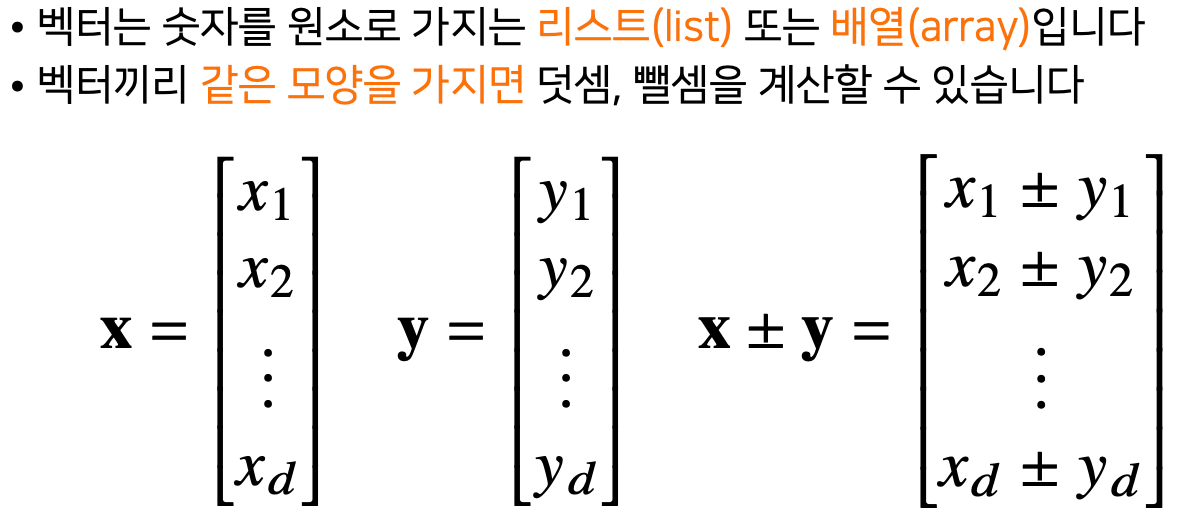
• 같은 모양을 가지지 않은 벡터끼리는 덧셈/뺄셈/곱셈이 불가능
• 벡터를 가지고 연산을 할때는 벡터의 차원의 갯수를 중요하게 생각해야한다!!

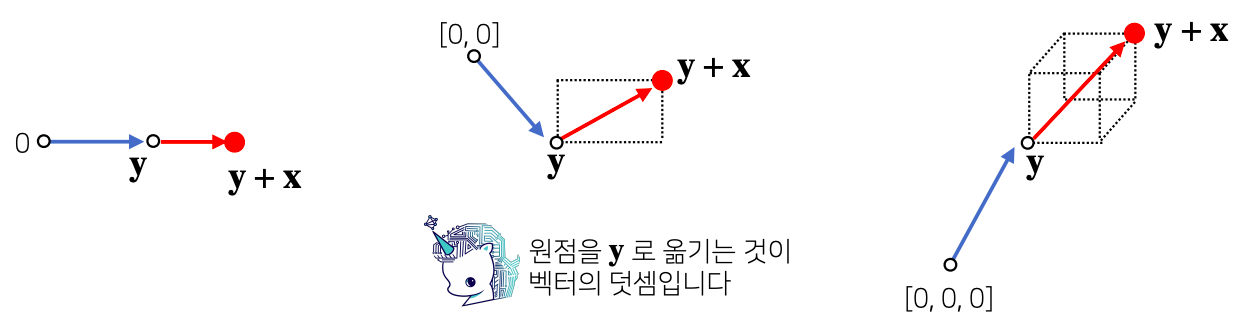
• 벡터의 덧셈이 공간상에서 어떻게 표현되는지 확인!
  • 두 벡터의 덧셈은 다른 벡터로부터 상대적 위치이동 을 표현
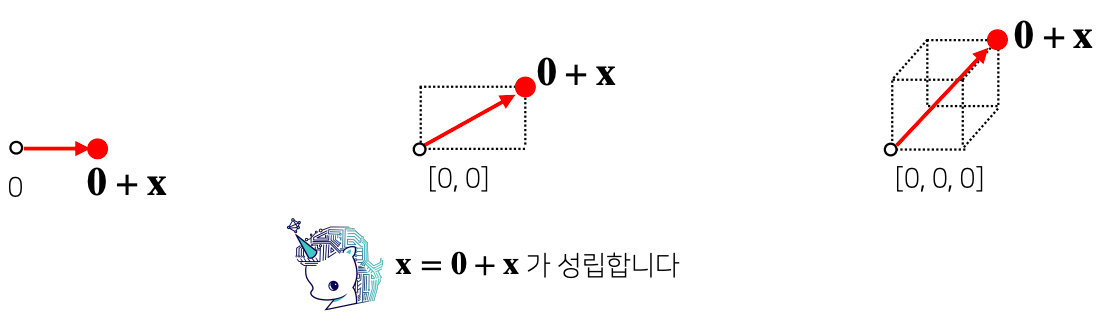
  • 원점을 0벡터라고 부르게 되면 원래 벡터 x는 0벡터 + x 즉, 0벡터 + x 로 표시할 수 있다
  • 즉, 원점에서 x 라는 벡터로 향하는 화살표로 표현할 수 있다

• 0벡터에서 y+x 라는 벡터로 화살표를 새로 그리게 됬을 때 결과물이 y + x 벡터

벡터의 노름(norm) 구해보기

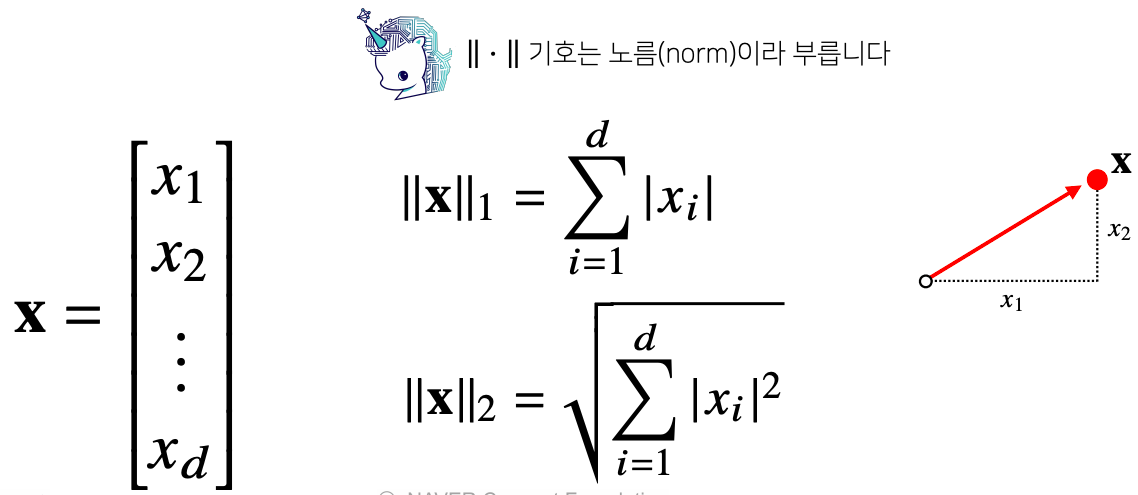
• 벡터의 노름(norm)은 원점에서부터의 거리 를 말한다
  • 주어진 벡터가 어떤 공간상에서 한 점을 표현한다고 했을 때 벡터의 노름은 원저에서부터 그 한 점 사이의 거리를 표현
  • 벡터는 여러 종류의 노름이 정의가 되어있다
  • 아래와 같이 주어진 벡터 x가 있을 때 x의 노름이 보통 두 가지 종류로 표현할 수 있는데
    • 하나는 x의 L1 노름으로 첫번째 1 이라는 기호로 표시되어 있는 첫번째 L1 노름
    • 두번째는 x의 L2 노름으로 두번째 2 라는 기호로 표시되어 있다

• 노름 이라는 기호는 1,2,3 차원을 성립하는 것이 아니라 임의의 차원 d에 대해서 성립한다는 것을 명심!

  • 거리를 계산할 때는 1,2,3 차원에서 거리를 계산하는걸 보통 많이 생각하는데
  • 거리는 임의의 차원에서 계산할 수 있는것이기 때문에 벡터의 노름은 벡터의 차원의 갯수와 상관없이(구성 성분 원소의 갯수와 상관없이) 계산할 수가 있다

• L1 : 노름은 각 성분의 변화량의 절대값 을 모두 더한다

  • x라는 벡터가 x1 ~ xd 까지가 정의가 되어있을때 각각의 구성성분의 절대값을 더해주는 것을 L1 노름이라고 한다
  • L1노름은 좌표평면에서 각 좌표축을 따라서 움직이는 거리들로 이해하면 된다
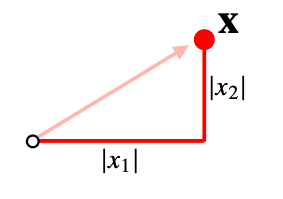
  • 2차원 좌표평면에서는 x축을 따라서 이동하게되는 x1의 절대값 그리고 y축을 따라서 이동하게 되는 x2의 절대값으로 두 값을 더해주는것이 L1노름이다
  • 두 좌표측을 따라서 이동하는 거리를 L1노름이라고 정의를 한다

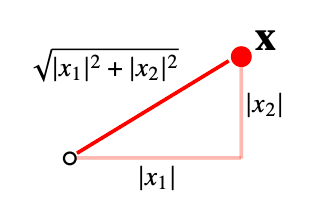
• L2 : 노름은 피타고라스 정리를 이용해 유클리드 거리를 를 계산한다
  • 원점에서 x라는 벡터로 직접 바로 연결되는 선의 거리를 L2노름
  • 2차원 좌표평면 뿐만 아니라 d차원 좌표평면상에서의 L2노름 값을 정의를 할 수 있기 때문에 임의의 차원에서도 유클리드 거리를 계산할 수 있다.

!

• 왜 다른 노름을 소개하나요?
  • 노름의 종류에 따라 기하학적 성질 이 달라진다
  • 서로 다른 노름을 사용하게 되면 거리라는 개념이 달라지기 때문에 원이라는 정의 자체가 원점에서 부터의 거리로 정의되는 것이라서 거리라는 개념을 다르게 정의를 하게 되면 당연히 기하학적 모양이 바뀐다
  • 그래서 같은 좌표평면이라 하더라도 노름을 다르게 사용함에 따라 기하학적 성질이 달라지기 때문에 성질이 달라진 어떤 기하 세계에서 보통 학습을 진행하게 될때는 굉장히 다른 성질들이 성립하게 되서 이런 다른 성질들을 이용해서 기계학습에서 다양한 종료의 학습방법, 정규화 방법들을 사용할 때 응용할 수 가 있다
  • 머신러닝에서는 서로 굉장히 다른 노름들을 사용해서 최적화를 하거나 학습할때 이용하기 때문에 잘 이해하자!
  • 각 기계학습 방법론에서 어떤 노름을 사용할지 정할 때, 기하학적 성질들에 많이 의존한다.
  • 그렇기 때문에 기하학적 성질에 따라서 노름이 결정된다는 것을 이해하자!
  • 머신러닝에선 각 성질들이 필요할 때가 있으므로 둘 다 사용한다

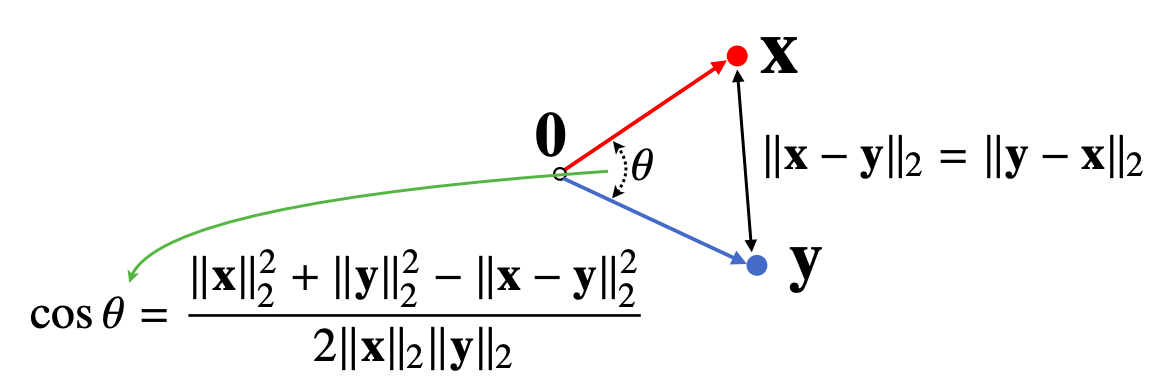
• 두 벡터 사이의 거리를 구해보자
  • L1, L2 - 노름을 이용해 두 벡터 사이의 거리 를 계산할 수 있다
  • 개념 : 두 점이 주어졌을때 두 점 사이의 거리를 계산
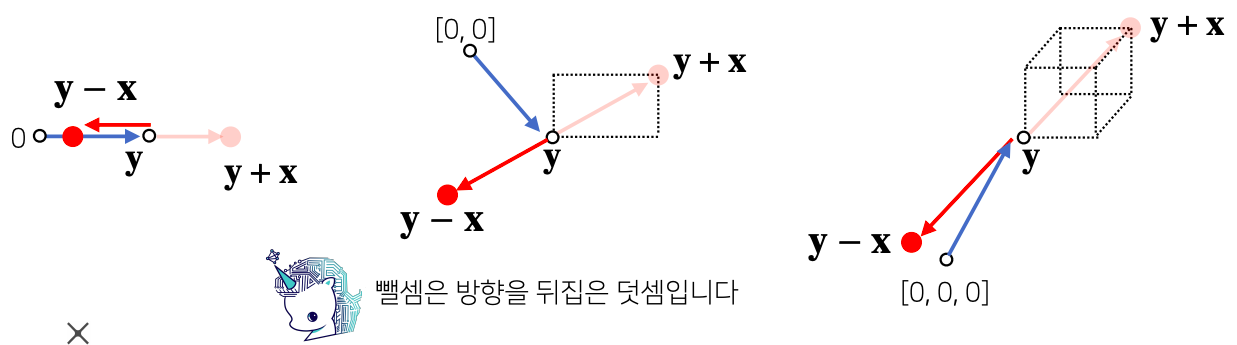
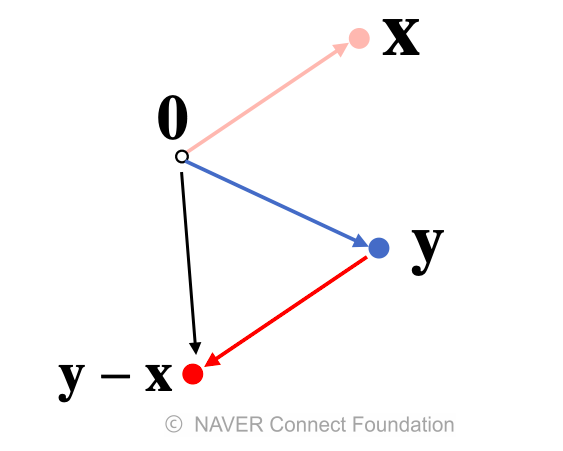
  • 두 벡터 사이의 거리를 계산할 때는 벡터의 뺄셈 을 이용한다
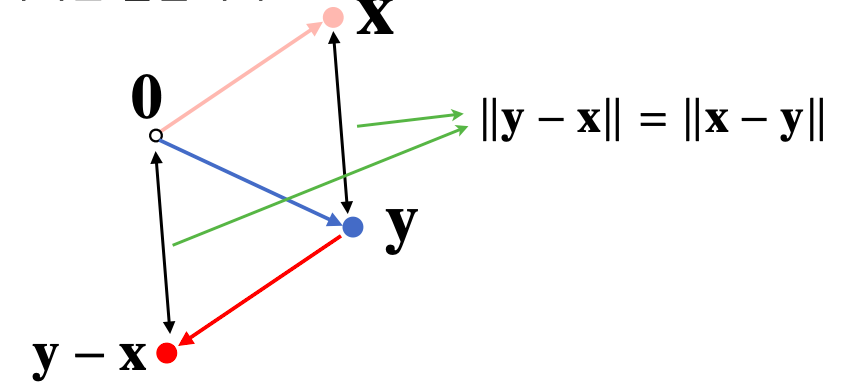
  • 0벡터에서 y-x벡터로 이동하는 화살표에 거리가 사실은 아래에 보이는 x라는 벡터의 점에서 y라는 점으로 이동하는 거리와 일치
  • 뺄셈은 거꾸로 해도 거리는 같다

• 두 벡터 사이의 각도 구해보기
  • 두 벡터 사이의 거리를 이용하여 각도도 계산 할 수 있다
  • 단, 각도는 L1 노름이 아니고 L2노름에서만 계산이 가능하다
  • 먼저 두 벡터 사이의 거리를 계산할 때 L2 노름으로 계산을 하게 되면 피타고라스의 정리에 의해서 유클리드 거리를 계산할 수 있다.
  • 유클리드 거리를 계산해서 두 점 사이의 거리를 계산할 수 있다면 0벡터와 x벡터와 y벡터로 이루어진 삼각형과 제2 코사인 법칙을 이용해서 두 벡터사이의 각도를 계산할 수 있다
  • 분자를 쉽게 계산하는 방법이 내적 이다

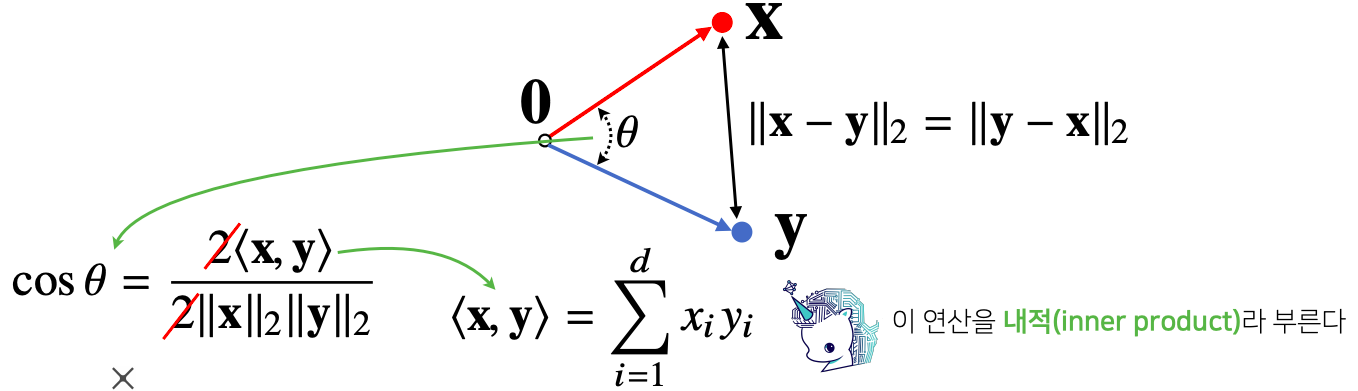
def angle(x,y):
    v = np.inner(x,y) / (12_norm(x) * 12_norm(y))
    theta = np.arccos(v)
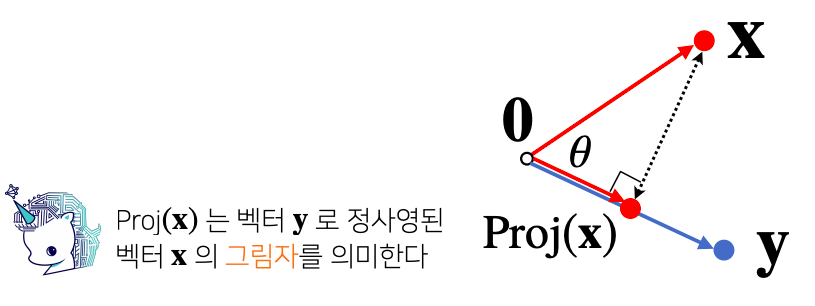
    return theta

• 내적은 어떻게 해석할까 ?
  • 내적은 정사영(orthogonal projection) 된 벡터의 길이와 관련 있다
  • 정사영 : x라는 벡터랑 y라는 벡터가 그림상에 있을 때 x벡터에 y벡터상에서의 그림자를 표현
  • proj(x) : x벡터에 y벡터로 정사영된 벡터x의 그림자
  • proj(x)의 길이는 코사인법칙 에 의해 ∥x∥ cos θ 가 된다
  • 내적은 정사영의 길이를 벡터y의 길이 ∥y∥만큼 조정한 값이다
  • 내적은 두 벡터사이의 유사도를 측정하는데 많이 사용한다

행렬

• 행렬의 개념과 연산, 그리고 벡터공간에서 가지는 의미를 설명
• 연립방정식 풀기와 선형회귀분석에 응용하는 방법 소개
• 벡터의 확장된 개념인 행렬은 행(row)벡터를 원소로 가지는 2차원 배열로 벡터와 다르게 계산되는 연산들에 주의
• 행렬연산은 딥러닝에서 가장 핵심적인 연산이라고 볼 수 있을만큼 중요하고, 자주 사용되기 때문에 행렬 연산의 메커니즘, 그리고 이 때 가지는 기하학적 의미와 머신러닝에서 어떻게 사용되는지를 충분히 이해하고 넘어가자

• 행렬(matrix)은 벡터를 원소를 가지는 2차원 배열

• 보통 열 벡터를 원소로 가지는 2차원 배열이지만 파이썬에서 넘파이를 이용할 때는 행 벡터를 원소로 가지는 2차원 배열로 이해를 하자

  • 행렬의 곱셈을 이해할때 좀 더 명확하게 계산할 수 있기 때문
  • 행렬은 행(row)과 열(column)이라는 인덱스(index)를 가진다
    • X(행, 열)
  • 행렬의 특정 행(열)을 고정하면 행(열)벡터라 부른다

• 행렬의 전치행렬 (Transpose)

  • 행과 열의 인덱스가 바뀐 행렬을 말한다
  • n x m 행렬 = m x n 행렬

• 행렬을 이해하는 방법 (1)

  • 벡터가 공간에서 한 점을 의미한다면 행렬은 여러 점들 을 나타낸다
  • 행렬의 행벡터 xi 는 i번째 데이터를 의미한다
  • 행렬의 xij 는 i 번째 데이터의 j__ 번째 변수의 값 을 말한다
  • 여러점들을 나타내는 걸로 사용할 수 있기 때문에 데이터들의 모임이라고 이해하면 쉽다

• 행렬의 덧셈, 뺄셈, 성분곱, 스칼라곱

  • 행렬은 벡터를 원소로 가지는 2차원 배열이다
  • 행렬끼리 같은 모양을 가지면 덧셈, 뺄셈을 계산할 수 있다
  • 성분곱 은 벡터와 똑같다
  • 스칼라곱 도 벡터와 차이가 없다

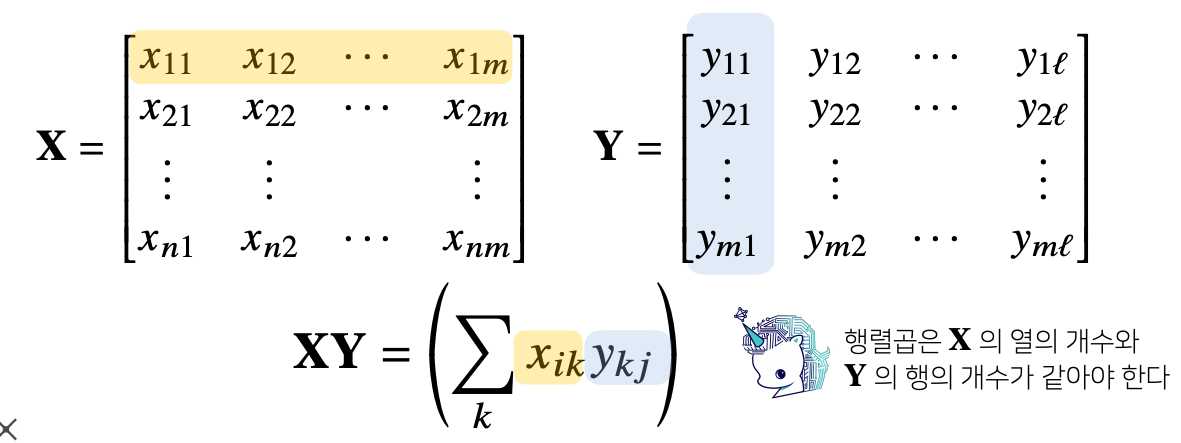
• 행렬 곱셈

  • 행렬 곱셈 (matrix multiplication)은 i 번째 행벡터와 j 번째 열벡터 사이의 내적 을 성분으로 가지는 행렬을 계산
  • X행렬의 열의 갯수와, Y 행렬의 행의 갯수가 같아야 계산이 가능하다
    • 결과의 shape은 n x m @ j x k = n x k 가 된다

• 행렬도 내적이 있을까?
  • 넘파이의 np.inner는 i 번째 행벅터와 j번째 행벡터사이의 내적을 성분으로 가지는 행렬을 계산한다
  • 수학에서 말하는 내적과는 다르므로 주의!

• 행렬을 이해하는 방법 (2)
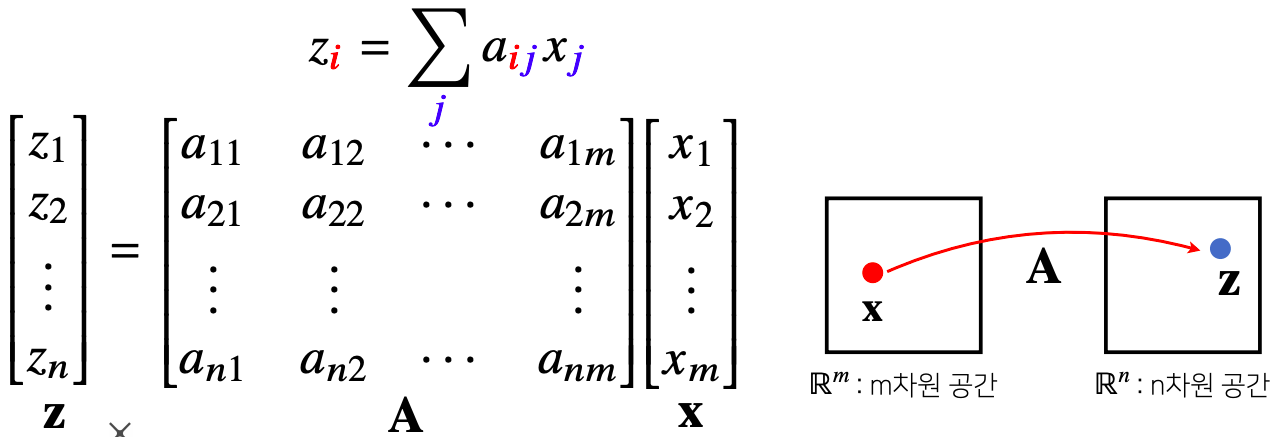
  • 행렬은 벡터공간에서 사용되는 연산자(operator) 로 이해
  • 행렬곱은 통해 벡터를 다른 차원의 공간 으로 보낼 수 있다
  • z벡터 x벡터를 a라는 행렬을 통해서 이어줄 수 있다
    • 이렇게 이어주는 함수의 역할을 연산자라고 이해하면 된다
    • 여기서 z벡터와 x벡터는 같은 걸 가르킨다 다만 차원이 다를뿐
      예: 한국에선 - 정훈, 미국에선 - David
  • 행렬곱을 통해 패턴을 추출 할 수 있고 데이터를 압축 할 수도 있다

• 역행렬 이해하기
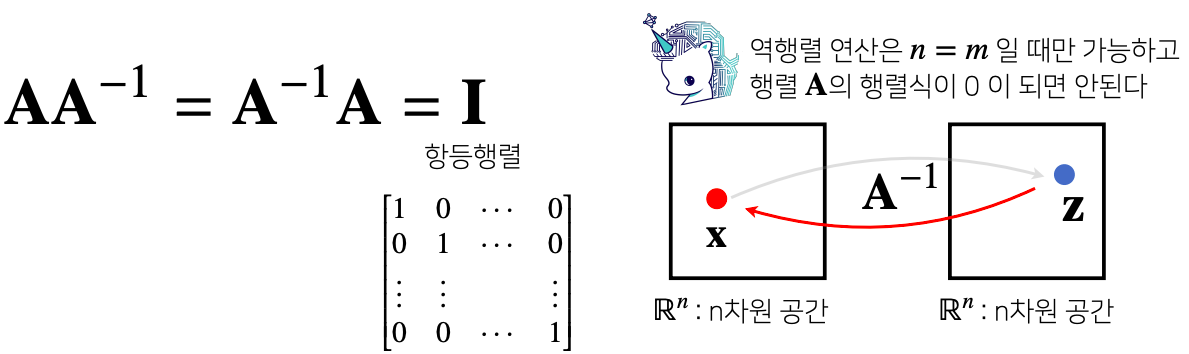
  • 어떤 행렬 A의 연산을 거꾸로 되돌리는 행렬을 역행렬(inverse matrix) 이라고 부르고 A^-1 라 표기한다
  • 역행렬은 행과 열 숫자가 같고 행렬식(determinant)이 0이 아닌 경우 에만 계산할 수 있다
  • 행렬곱은 순서가 민감하지만 역행렬에 대해서는 순서에 상관없이 A라는 생렬에다 역행렬(A^-1)을 곱해줬을 때는 항등행렬 이 결과값을 나온다
  • 항등행렬: 임의의 벡터 또는 행렬을 곱해줬을때 자기자신이 나오게되는 행렬

import numpy as np

X = np.array([[1,-2,3],[7,5,0],[-2,-1,2]])
np.linalg.inv(X) # X의 역행렬 
X @ np.linalg.inv(X)

• 만일 역행렬을 계산할 수 없다면 유사역행렬(pseudo-inverse) 또는 무어 펜로즈(Moore_Penrose) 역행렬 A^+ 을 이용한다
  • 행과 열의 숫자가 달라도 사용 가능
  • m차원 공간상에 존재하는 벡터 x와 n차원 공간상에 존재하는 벡터 z를 연결하는 연산자 a가 있을때, 차원을 다시 되돌리기 위해 유사 역행렬을 이용해서 굉장히 많은 기계학습 또는 통계학을 살펴 볼 수 있다
  • 행과 열의 갯수가 다를때 기능이 조금 다르다
    • 만약 행이 열보다 많을때 유사 역행렬은 원래 행렬보다 더 먼저 곱해줘야 항등행렬이 나온다
    • 만약 열이 행보다 많을때 유사 역행렬은 원래 행렬보다 더 뒤에 곱해줘야 항등행렬이 나온다
    • 유사 역행렬을 가지고 항등행렬을 계산할 때는 위에 사항을 주의해야한다!!

Y = np.array([[0,1],[1,-1],[-2,1]])

np.linalg.pinv(Y)
np.linalg.pinv(T) @ Y

• 응용1: 연립방정식 풀기

  • np.linalg.pinv를 이용하면 연립방정식의 해를 구할 수 있다.
  • n <= m 인 경우 : 식이 변수 개수보다 작거나 같아야 함

• 응용2: 선형회귀분석

  • np.linalg.pinv 를 이용하면 데이터를 선형모델(linear model)로 해석 하는 선형회귀식 을 찾을 수 있다
  • n >= m 인 경우 : 데이터가 변수 개수보다 많거나 같아야 함
  • Moore_Penrose 역행렬을 이용하면 y에 근접하는 y_hat을 찾을 수 있다