[Contents]
1) 경사하강법(순한맛)
2) 경사하강법(매운맛)
경사하강법(순한맛)
- 미분의 개념과 그래디언트 벡터 에 대해 설명
- 경사하강법 의 알고리즘과 실제 코드에서의 구현을 보여준다
- 접선의 기울기를 이용해서 함수의 최솟값으로 점을 이동시키는 원리를 알면 이를 바탕으로 경사하강법의 알고리즘과 수식을 이해할 수 있다
- 특히 변수가 벡터인 경우, 편미분을 통해서 구한 그래디언트 벡터를 통해 d- 차원으로 경사하강법을 확장할 수 있다는 개념을 확실하게 잡자
미분이 뭔가요?
- 미분(differentiation)은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구 로 최적화에서 제일 많이 사용하는 기법
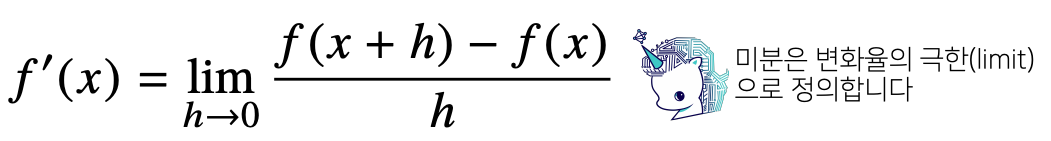
import sympy as sym
from sympy.abc import x
sym.diff(sym.poly(x**2 + 2*x + 3), x) # Poly(2*x + 2, x, domain='zz')미분을 그림으로 이해해보자
- 미분은 함수 f의 주어진 점 (x,f(x)) 에서의 접선의 기울기 를 구한다
- 미분을 계산하려면 함수의 모양이 매꾸러워야(연속) 한다
- 아래 함수에서 h를 0으로 보내면 (x, f(x))에서 접선의 기울기로 수렴한다
- 한 점에서 접선의 기울기를 알면 어느 방향으로 점을 움직여야 함수값이 증가 하느지/감소 하는지 알 수 있다
- 고차원 공간(10차원, 1억차원 등등)에서도 미분을 사용하면 어느방향으로 움직여야 함수값이 증가/감소 할지 알수가 있기 때문에 미분을 이용해서 함수를 최적화한다
- 증가 시키고 싶다면 미분값을 더하고
- 감소 시키고 싶으면 미분값을 뺍니다
- 미분값을 더하면 경사상승법(gradient ascent) 이라 하면 함수의 극대값 의 위치를 구할 때 사용한다
- 미분값을 빼면 경사하강법(gradient descent) 이라 하면 함수의 극소값 의 위치를 구할 때 사용한다
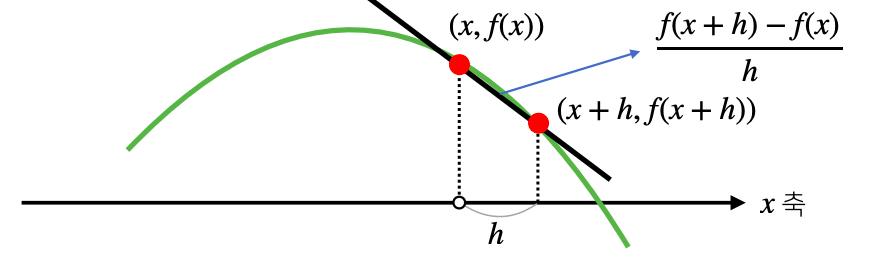
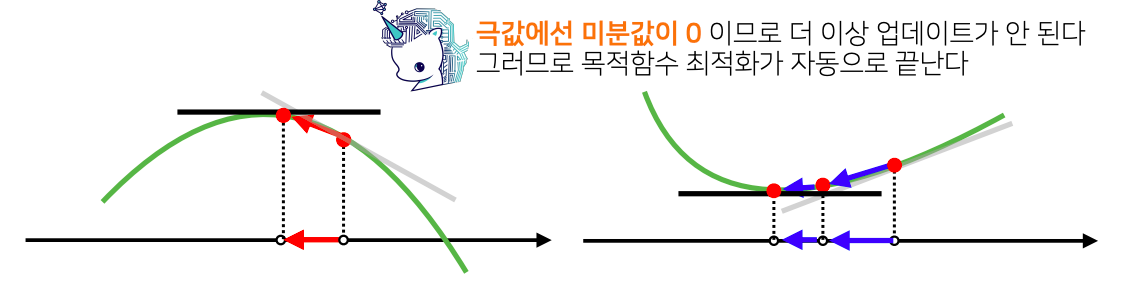
- 경사상승/경사하강 방법은 극값에 도달하면 움직임이 멈춘다
- 극값에선 미분값이 0 이므로 더 이상 업데이트가 되지 않는다. 그러므로 목적함수 최적화가 자동으로 끝난다
경사하강법 : 알고리즘
- 컴퓨터로 계산할 땐 미분이 정확히 0이 되는 것은 불가능하므로 eps 보다 작을 때 종료하는 조건이 필요하다
- var = var - lr * grad - 이 부분이 x - λf′(x)dㅡㄹ 계산하는 부분. lr 은 학습률로서 미분을 통해 업데이트하는 속도를 조절한다
- 주의사항! : 학습률 같은 경우 조심해서 제어해야만 경사하강 알고리즘이 수렴 여부를 결정한다
- grad = gradient(var) - 종료조건이 성립하기 전까지 미분값을 계속 업데이트한다

변수가 벡터이면요?
- 벡터가 입력인 다변수 함수의 경우 편미분(partial differentiation) 을 사용한다
- i번째 방향(변수)에서의 변화율만 계산할 수 있기 때문에 변수가 벡터인 경우에도 편미분을 이용해서 경사하강법 알고리즘을 똑같이 사용가능하다


- 그레디언트 벡터를 사용하게 되면 수직선상에서 업데이트, 위에서 배운 경사하강법, 가 아닌 일반적인 d 차원 공간에서 벡터에 적용되는 경사하강법을 똑같이 사용 가능하다
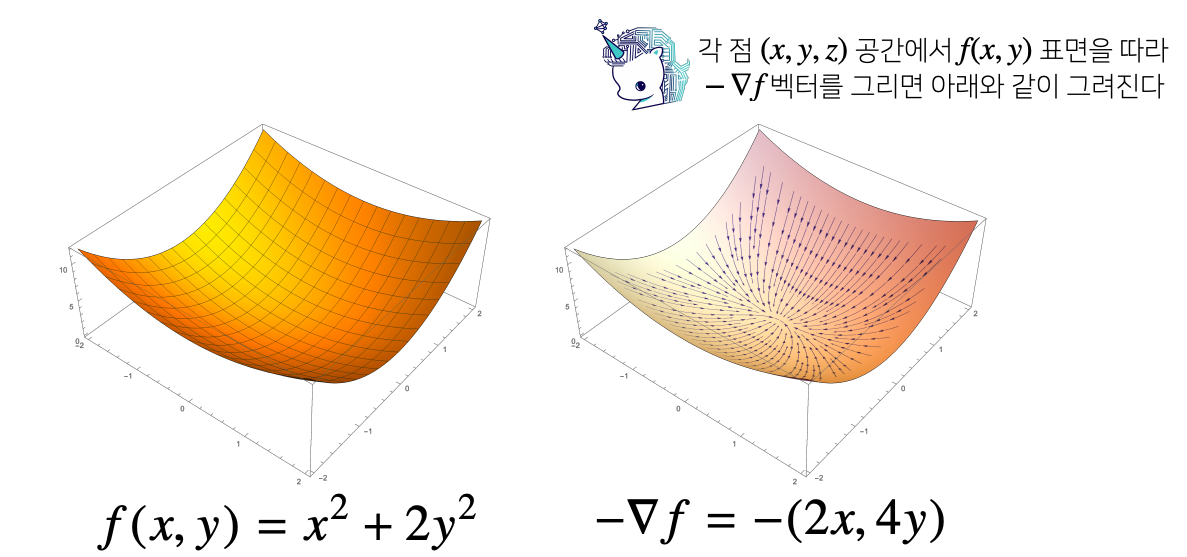
- (x, y, z) 라는 3차원 공간상에서 f(x, y) 표면에 따라서 그레디언트 벡터에 마이너스(-)를 붙이게 되면 오른쪽 그림과 같이 f(x, y)의 최소점(극소점)으로 향하는 화살표들의 움직임으로 볼 수 있다
- f(x, y)의 어떤점에서 출발을 하든 마이너스(-) 그레디언트 f 방향으로 따라가기만 하면 f(x, y)의 최소점으로 흐른다
경사하강법: 알고리즘
- 앞에서는 그레디언트 즉, 미분값의 절대값을 계산했지만 이제는 그레디언트는 벡터이기 때문에 절대값을 계산할 순 없고 대신에 노름(norm)을 계산해서 종료조건을 설정해준다.
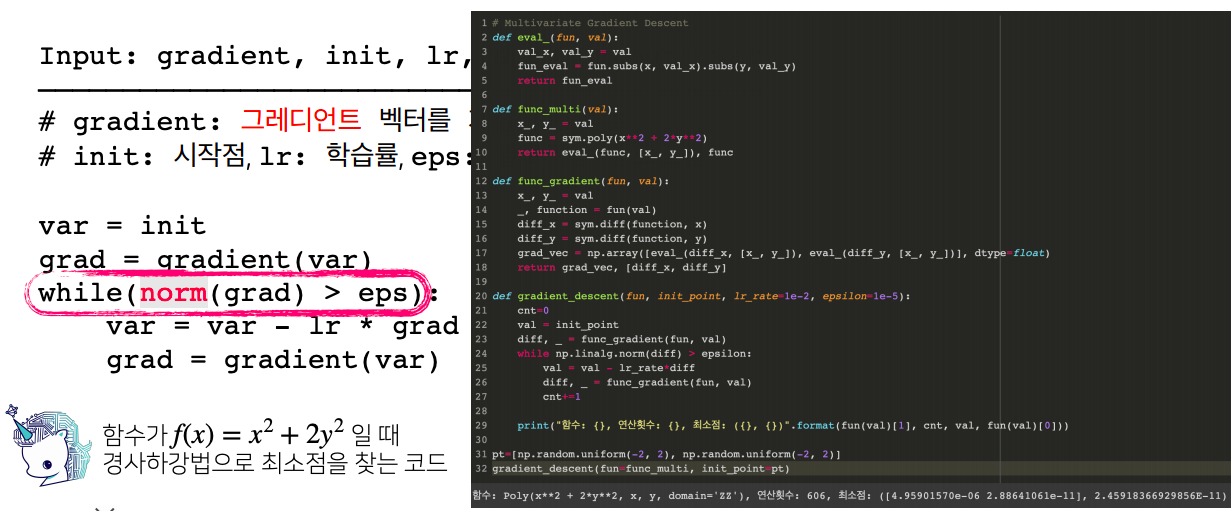
경사하강법(매운맛)
- 경사하강법 기반의 선형회귀 알고리즘에 대해 설명
- 경사하강법의 단점을 보완하는 확률적 경사하강법(stochastic gradient descent) 을 소개
- 무어-펜로즈 역행렬을 확용한 선형회귀분석과 비교하여, 선형 모델 외에도 적용 가능한 경사하강법-선형회귀분석 방법 을 성명. 이 때 나오는 경사하강법 알고리즘 수식을 정확히 이해하고 넘어가자!
- 딥러닝에서 경사하강법이 가지는 한계를 설명하고, 이를 극복하기 위한 확률적 경사하강법을 소개
선형회귀분석 복습
- np.linalg.pinv 를 이용하면 데이터를 선형모델(linear model)로 해석하는 선형회귀식 을 찾을 수 있다
- n개의 데이터로 이루어져있는 상황에서 데이터를 가장 잘 표현하는 선형모델을 찾는 모델을 선형회귀분석이라고 한다
- 무어-펜로즈 역행렬을 이용하게 되면 주어져있는 데이터의 정답에 해당하는 y랑 가장 근사적으로 가까운 서형모델을 찾을수가 있다
- 이번에는 무어-펜로즈 역행렬을 이용하지 않고 경사하강법 알고리즘을 이용해서 선형모델을 찾는 모델을 설명
경사하강법으로 선형회귀 계수 구하기
- 두 벡터의 차이의 L2노름을 최소화하는 beta를 찾는것이 선형회귀분석의 목적
- beta를 최소화 하고 싶다면 목적식을 beta로 미분을 한다음에 주어진 beta에서 미분값을 빼면 경사하강법 알고리즘으로 최소의 해당하는 점을 구할 수 있다

- 위에서 조심해야 할 점은 원래 사용되는 L2 노름과 차이가 있다
- 위에서 사용되는 L2 노름은 n개의 데이터를 가지고 계산되는 L2의 노름이기 때문에 i = 1 부터 n 까지 더해준 다음에 제곱근을 취해주는것이 아니고 i = 1 부터 n 까지 더해준다음에 평균값을 계산해주기 위해서 1/n로 나눠준 후에 제곱근을 구해줘야한다
경사하강법 기반 선형회귀 알고리즘
# input : X, y, lr, T, Output : beta
# norm : L2 - norm을 계산하는 함수
# lr : 학습률 , T : 학습횟수
for t in range(T): # 종료조건을 일정 학습횟수로 변경한 점만 빼고 앞에서 배운 경사하강법 알고리즘과 같다
error = y - X @ beta
grad = -transpose(X) @ error
beta = beta - lr * grad- 이제 경사하강법 알고리즘으로 역행렬을 이용하지 않고 회귀계수를 계산할 수 있다
- 아래 코드는 경사하강법 알고리즘을 이용해서 선형모델로 데이터를 생성하고 그때 계수를 찾는 예제
- 여기서 사용된 계수는 두 번째줄에서 보듯이 1과 2라는 계수로 만들어냈고 y절편은 3을 이용해서 데이터를 생성. 그래서 찾아야 되는 계수는 1과 2 그리고 3
- 선형모델의 계수를 가지고 만들어낸 데이터를 이용해서 경사하강법 알고리즘으로 계수를 찾아보는 알고리즘을 보면 원래 데이터를 생성할 때 사용한 계수 1과 2와 3에 근접하다는 것을 확인할 수 있다
- 주의 ! - 경사하강법 알고리즘은 무어 - 펜리즈 역행렬을 이용하는 것 처럼 정확한 값을 도달하는 것처럼 계속해서 수렴하는 것이 아니기 때문에 학습 횟수를 너무 작게 잡게되면 목표로 하는 계수를 찾지 못할수 있다
- 따라서 학습 횟수와 학습률을 적절하게 선택해야 한다
X = np.array([[1,1],[1,2],[2,2],[2,3]])
y = np.dot(X, np.array([1,2]))+3
beta_gd = [10.1, 15.1, -6.5] # [1,2,3] 이 정답
X_ = np.array([np.append(x.[1]) for x in X]) # intercept 항 추가
for t in range(100): # 학습횟수 (hyper parameter)
error = y - X_ @ beta_gd
# error = error / np.linalg.norm(error)
grad = -np.transpose(X_) @ error
beta_go = beta_gd - 0.01 * grad
print(beta_gd) # [1.00000367, 1.99999949, 2.99999516]경사하강법은 만능일까?
- 이론적으로 경사하강법은 미분가능하고 볼록(convex)한 함수에 대해선 적절한 학습률과 학습횟수를 선택했을 때 수렴이 보장 되어 있다
- 특히 선형회귀의 경우 목적식에 L2 노름을 사용하게 되는데 이 L2 노름을 사용한 목적식은 회귀계수 beta에 대해서 볼록함수 이기 때문에 알고리즘을 충분히 돌리면 수렴이 보장된다
- 하지만 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있으므로 수렴이 항상 보장되지는 않다
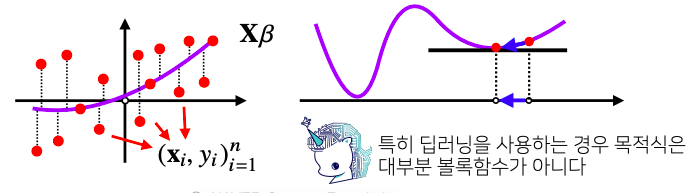
- 그렇기 때문에 경사하강법을 딥러닝에 사용할때는 변형된 경사하강법 알고리즘을 사용해야한다
확률적 경사하강법
- 확률적 경사하강법(stohastic gradient descent) 은 모든 데이터를 사용해서 업데이트하는 대신 데이터 한개 또는 일부 활용하여 업데이트한다
- 볼록이 아닌 (non-convex) 목적식은 SGD를 통해 최적화활 수 있다
- SGD 라고 해서 만능은 아니지만 딥러닝의 경우 SGD가 경사하강법보다 실증적으로 더 낫다 고 검증되었다
- SGD는 데이터의 일부를 가지고 parameter를 업데이트하기 때문에 연산자원을 좀 더 효율적으로 활용하는데 도움이 된다
- 만약에 모든 데이터(n)를 사용해서 gradient vector를 계산하게 되면 연상량이 d^2(n) 이 되는데
- 모든 데이터가 아니라 일부 b개의 미니배치만 사용하게 되면 (b)d^2 만큼 줄어든다
- 이때 계산되는 gradient vector는 경사하강법을 통해서 계산되는 gradient vector랑 동일하진 않을수 있지만 확률적으로 기대값의 관점으로는 원래 gradient vector랑 유사하게 사용할 수 있다
확률적 경사하강법의 원래 : 미니배치 연산
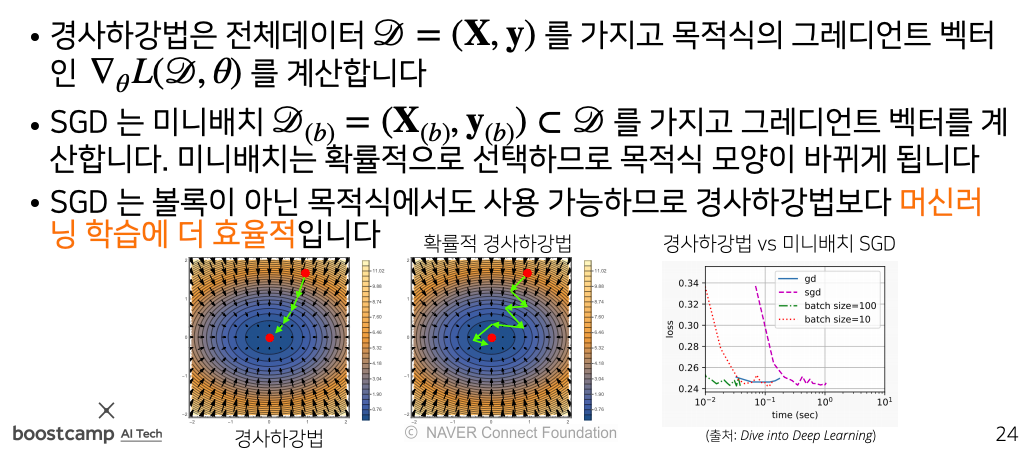
- 데이터를 가지고 gradient vector를 계산해서 움직이기 때문에 최소점으로 향하는 움직임은 똑같다
- 경사하강법은 모든 데이터를 가지고 gradient vector를 계산하는 반면 확률적 경사하강법은 미니배치를 가지고 gradient vector를 계산하므로 연산 속도가 훨씬 더 빠르다
확률적 경사하강법의 원리: 하드웨어
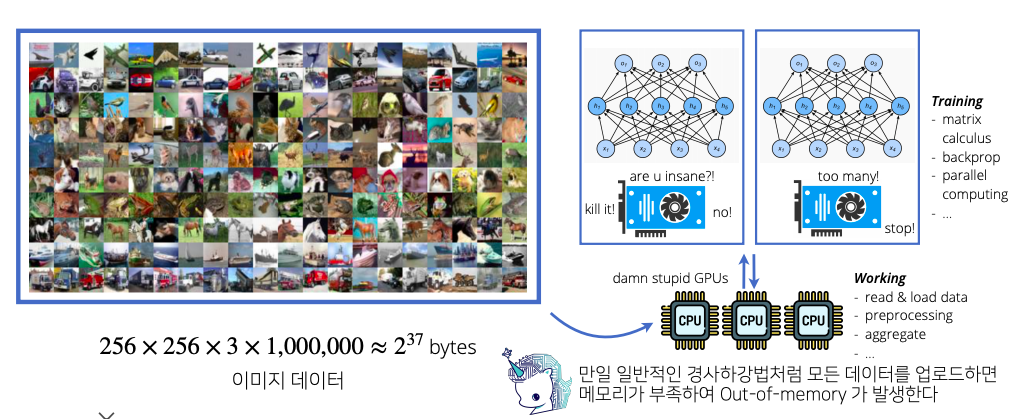
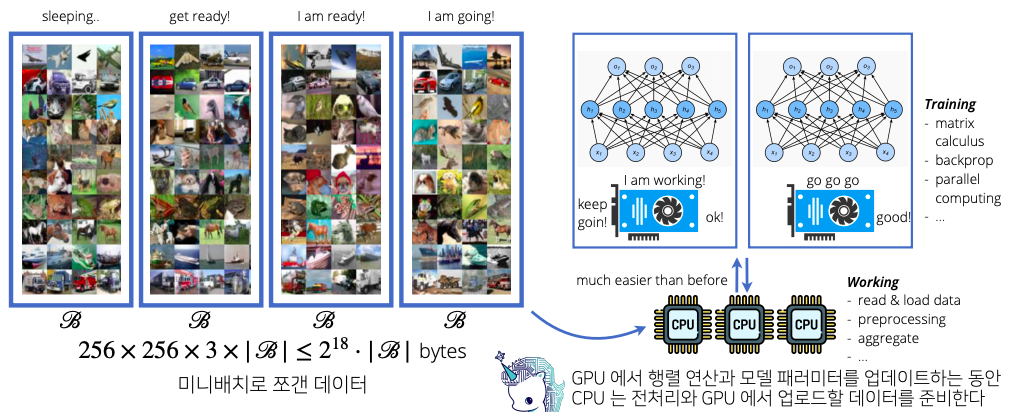
- 확률적 경사하강법은 알고리즘의 효율성과 하드웨어를 고려했을때 반드시 필수적인 알고리즘이다
