[Contents]
1) CNN 첫걸음
CNN 첫걸음
- Convolution 연산 과 다양한 차원에서의 연산방법 을 소개
- Convolution 연산의 역전파 에 대해 설명
- Convolution 연산은 오늘날 굉장히 많은 모델에서 이미지나 영상을 처리하기 위해 사용된다
- 지금까지 배웠던 fully connected layer와 비교해서 CNN(Convolutional Neural Network)의 커널 연산이 가지는 장점과, Convolution 여난이 다양한 차원에서 어떻게 진행되는지를 이해하자
- Convolution 연산의 경우, 커널의 모든 입력데이터에 대해 공통으로 적용이 되기 때문에 역전파를 계산하는 경우에도 똑같이 Convolution 연산이 나오게 된다
- 그림과 함께 잘 설명되어 있기 때문에 커널을 통해 gradient가 어떻게 전달이 되는지, 역전파가 어떻게 이루어지는지 짚고 넘어가자
Convolution 연산 이해하기
- 지금까지 배운 다층신경망(MLP)은 각 뉴런들이 선형모델과 활성함수로 모두 연결된 (fully connected) 구조였다
- 각 성분 에 대응하는 가중치 행 이 필요하다
- 만일 가 바뀌면 사용되는 가중치도 바뀐다
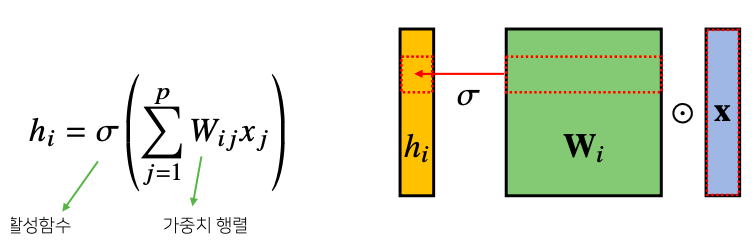
- convolution 연산은 이와 달리 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다
- : 활성함수
- : 커널 사이즈
- : 가중치 행렬
- 모든 에 대해 적용되는 커널은 로 같고 커널의 사이즈만큼 상에서 이동하면서 적용한다
- 활성화 함수를 제외한 Convolution 연산도 선형변화에 속한다
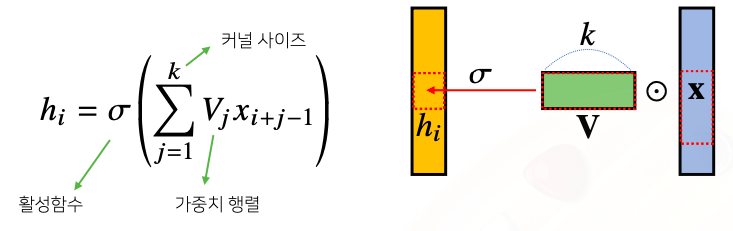
- Convolution 연산의 수학적인 의미는 신호(signal)를 커널을 이용해 국소적으로 증폭 또는 감소 시켜서 정보를 추출 또는 필터링하는 것이다
- continuous
- discrete
- convolution 을 수식으로만 이해하는 것은 매우 어렵다
- CNN 에서 사용하는 연산은 사실 convolution이 아니고 cross-correlation 이라 부른다
- continuous
- 커널은 정의역 내에서 움직여도 변하지 않고 (translation invariant) 주어진 신호에 국소적(local) 으로 적용한다
다양한 차원에서의 Convolution
- Convolution 연산은 1차원뿐만 아니라 다양한 차원에서 계산 가능하다
- 1D - conv :
- 2D - conv :
- 3D - conv :
- 데이터의 성격에 따라 사용하는 커널이 달라진다
- 차원이 높아진다 하더라도 i, j, k의 위치가 바뀌었을때 커널의 값은 바뀌지 않는다
2차원 Convolution 연산 이해하기
-
2D - conv 연산은 이와 달리 커널(kernel)을 입력벡터 상에서 움직여가면서 선형모델과 합성함수가 적용되는 구조이다
- : 커널
- : 입력
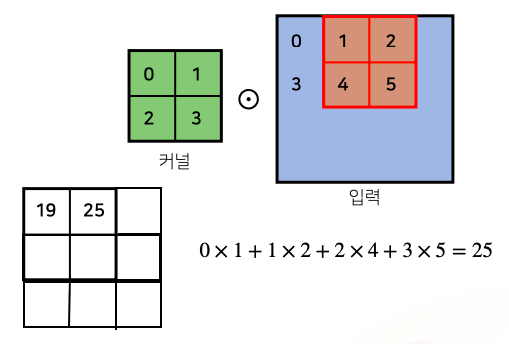
- 행렬연산을 하는것이 아니라 각각의 위치에 따라서 element-wise multiplication(성분곱)을 해서 더해주는 연산을 해준다
- 입력 크기를 , 커널 크기를 , 출력 크기를 라 하면 출력 크기는 다음과 같이 계산한다
- 가령 28x28 입력을 3x3 커널로 2D-Conv 연산을 하면 26x26이 된다
3차원 Convolution 연산 이해하기
- 3차원 Convolution 의 경우 2차원 Convolution을 3번 적용한다고 생각하면 된다
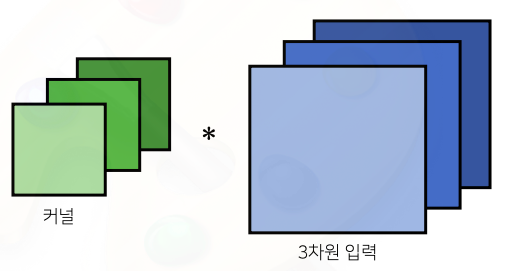
- 3차원 부터는 행렬이 아닌 텐서라 부른다
- 채널이 여러개인 경우 커널의 채널 수와 입력의 채널수가 같아야 한다
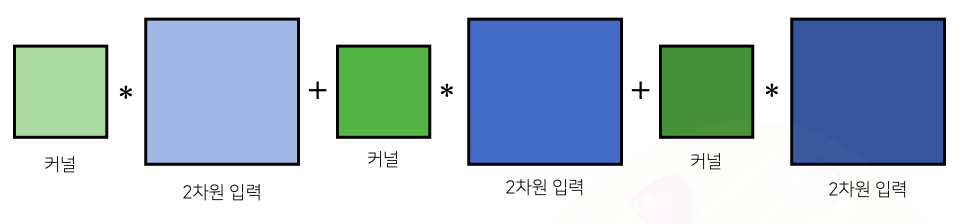
- 채널이 여러개인 2차원 입력의 경우 2차원 Convolution을 채널 개수만큼 적용한다고 생각하면 된다
- 텐서를 직육면체 블록으로 이해하면 좀 더 이해하기 쉽다
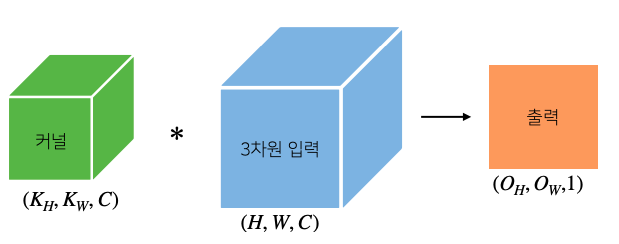
- 커널의 채널 개수와 입력의 채널개수를 같게 설정했기 때문에 애네들이 모두 convolution 연산 후 더해지기 때문에 출력에 해당하는 텐서의 3차원 차원은 1이 된다
- 커널을 개 사용하면 출력도 텐서가 된다
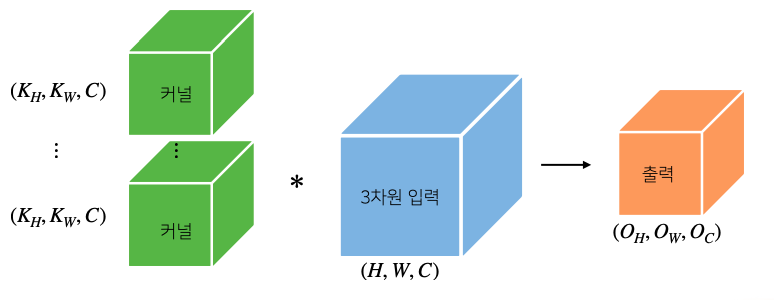
Convolution 연산의 역전파 이해하기
- Convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 된다
- discrete일 때도 마찬가지로 성립한다
- 그림으로 이해하면 훨씬 쉽다
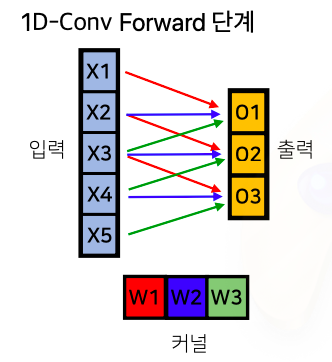
- 각 는 미분값을 의미한다
- 역전파 단계에서 다시 커널을 통해 gradient가 전달된다
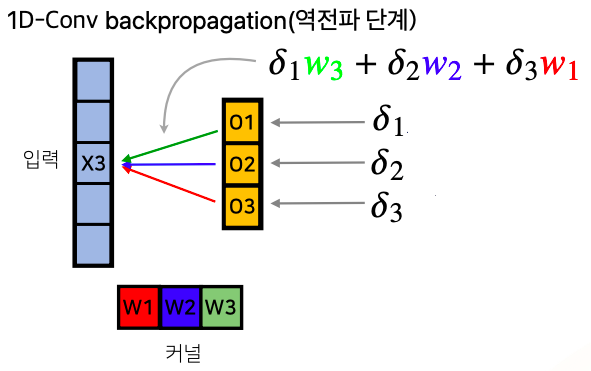
- 에서 각각 들이 적용될때 에는 가 적용됬고, 에는 가 적용됬고, 에는 이 적용된 사실을 위에서 확인할 수 있다
- 즉, 라는 입력이 각각 에서 적용이 될 때 사용되는 가중치에 따라서 gradient vector의 연결되는 가중치들이 대응되는 가중치들을 사용하게 된다
- 이와 같이 역전파 단계에서는 입력벡터에서는 곱해졌던 커널들을 통해서 gradient가 전달되게 된다
- 각각의 커널들은 어떻게 gradient가 전달되게 될까?
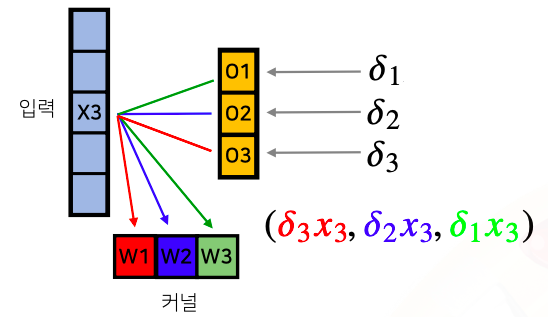
- 가 에 대해서 을 통해서 gradient를 전달했기 때문에 을 통해서 전달되었던 gradient인 는 으로 배당이 되는 대신 대신 를 곱해서 () 가 의 gradient로 전달 된다
- 도 위와 같은 방법을 생각해보자
- 각각의 커널들은 입력 뿐만 아니라 다른 입력에서도 적용됬기 때문에 이 gradient들은 다른 입력들에 적용됬던 gradient를 똑같이 전달되게 되서 아래와 같이 에는 이 를 통해서 전달됬고 는 , 는 로 전달됬다
- 때문에 이를 이용해서 각각의 들이 gradient를 통해서 전달이 되게 되는 것이고 이걸 통해서 들이 각각 에 해당하는 gradient 들을 다음과 같이 전달하게 되는 것이다
- 이 연산을 살펴보면 사실 gradient에 대한 convolution연산과 똑같이 나오게 되는 것이다