[Contents]

1) CNN - Convolution은 무엇인가?
2) Modern CNN - 1x1 convolution의 중요성
3) computer vision applications

CNN - Convolution은 무엇인가?

• CNN(Convolutional Neural Network)에서 가장 중요한 연산은 Convolution 이다
• CNN에 대한 공부를 하기 전에 Convolution의 정의, convolution 연산 방법과 기능 에 대해 배운다
• 입력을 축소하는 pooling layer, 모든 노드를 연결하여 최종적인 결과를 만드는 fully connected layer로 구성되는 기본적인 CNN 구조 에 대해 배운다
• 끝으로 Pytorch를 이용하여 CNN실습

Convolutional Neural Networks

• feature map : convolution을 통해 나온 값의 "뭉치"
• CNN은 Convolution layer, pooling layer, fully connected layer로 구성되어 있다
  • Convolution layer, pooling layer 의 효과 : 이미지에서 유용한 정보를 뽑아주는 feature extraction
  • fully connected layer 의 효과 : 분류, 회귀를 해서 원하는 출력값을 얻어주는 layer (decision making e.g., classification)
  • fully connected layer를 최소화 시키는 추세다
    • 학습시키고자 하는 모델의 파라미터의 수가 늘어나면 늘어날수록 학습이 어렵고 generalization performance(일반화 성능)가 떨어진다
    • 그렇기 때문에 같은 모델을 만들고 최대한 모델을 deep 하게 (convolution layer를 많이 가져간다) 가져가지만 동시에 파라미터의 숫자를 줄이는데 집중하게 된다
    • 정리 : 어떤 neural network을 봤을때 이 네트워크의 layer별로 몇개의 파라미터로 이루어져 있고 전체 파라미터의 숫자가 몇개있는지 아는것이 중요하다
• 파라미터의 숫자가 Convolution layer에 비해서 Dense layer로 넘어가면서 굉장히 많이 늘어난다
  • 그 이유는 Convolution operator가 각각의 하나의 커널이 모든 위치에 대해서 동일하게 적용되기 때문이다
  • 그래서 convolution operator는 일종에 shared parameter 이다

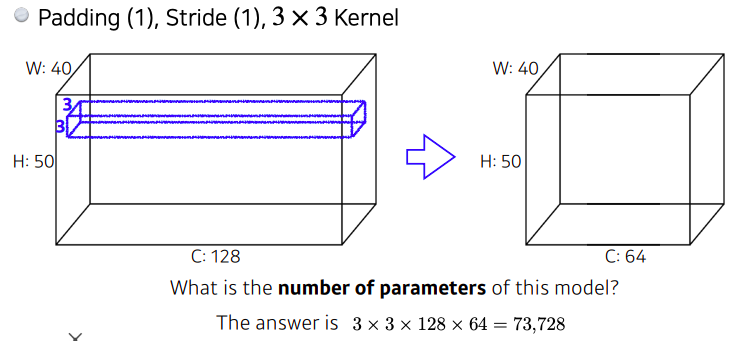
Convolution Arithmetic

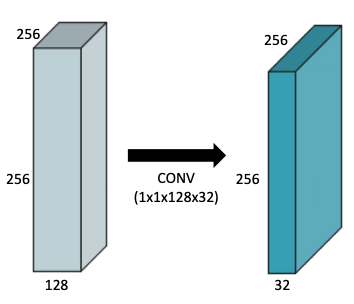
1x1 Convolution

why?

• 이미지에서 한 픽셀만 본다
• 차원 축소 (채널의 숫자를 줄인다)
• convolution layer는 깊게 쌓으면서 동시에 파라미터의 숫자는 줄이기 위해서

Modern CNN - 1x1 convolution의 중요성

• ILSVRC라는 Visual Recognition Challenge와 대회에서 수상을 했던 5개 Network 들의 주요 아이디어와 구조에 대해 배d운다
• AlexNet :
  • 최초로 Deep Learning을 이용하여 ILSVRC에서 수상
• VGGNet :
  • 3x3 Convolution을 이용하여 Receptive field는 유지하면서 더 깊은 네트워크를 구성
  • Receptive field 참고 자료
• GoogLeNet :
  • Inception blocks 을 제안
• ResNet :
  • Residual connection(Skip connection)이라는 구조를 제안
  • h(x) = f(x) + x 의 구조
• DenseNet :
  • Resnet과 비슷한 아이디어지만 Addition이 아닌 Concatenation을 적용한 CNN

Further Question

• modern CNN network의 일부는, Pytorch 라이브러리 내에서 pre-trained 모델로 지원한다. pytorch를 통해 어떻게 불러올 수 있을까?
  • 참고자료

AlexNet

key ideas

• ReLU Activation
  • linear model들이 갖는 좋은 성질들을 가지고 있다
    • gradient가 activation값이 커도 gradient를 그대로 가지고 있고 0보다 작을때는 0으로 바꾸어준다
    • easy to optimize w/ gradient descent
    • overcome the vanishing gradient problem
      • sigmoid, tanh 같은 activation function을 보면 slope가 0을 기점으로 값이 커지면 slope 가 점점 줄어든다
      • 즉, slope가 결국 gradient인데 가지고 있는 뉴런의 값이 많이 크면(0에서 많이 벗어나게 되면)
      • 그곳에서 나오는 gradient(slope)는 0에 가까워 진다
      • 그래서 vanishing gradient문제가 생기는데 ReLU는 이 문제를 해소해준다
• GPU 를 사용 (2 GPUs)
• Overlapping pooling
• Data augmentation
• Dropout

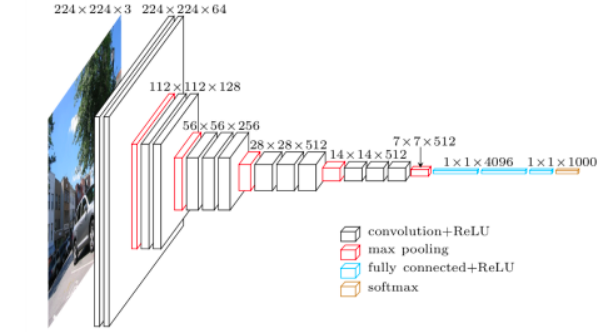
VGGNet

key takeaway

• 3 x 3 convolution 을 활용

why 3 x 3 convolution?

• convolution filter의 크기를 생각해 봤을때 크기가 커지므로써 가지는 이점은 :
  • convolution filter로 값을 찍었을때 고려되는 input의 크기가 커진다 (receptive field)
  • receptive field :
    • 하나의 convolution feature map 값을 얻기 위해서 고려할 수 있는 입력의 spatial dimension
    • 특정 feature 픽셀이 원본 영상의 "몇 필셀"이나 값을 대변할 수 있는지를 의미한다
  • 3 x 3 이 두번 이뤄지게 되면 receptive field 는 5 x 5 가 된다

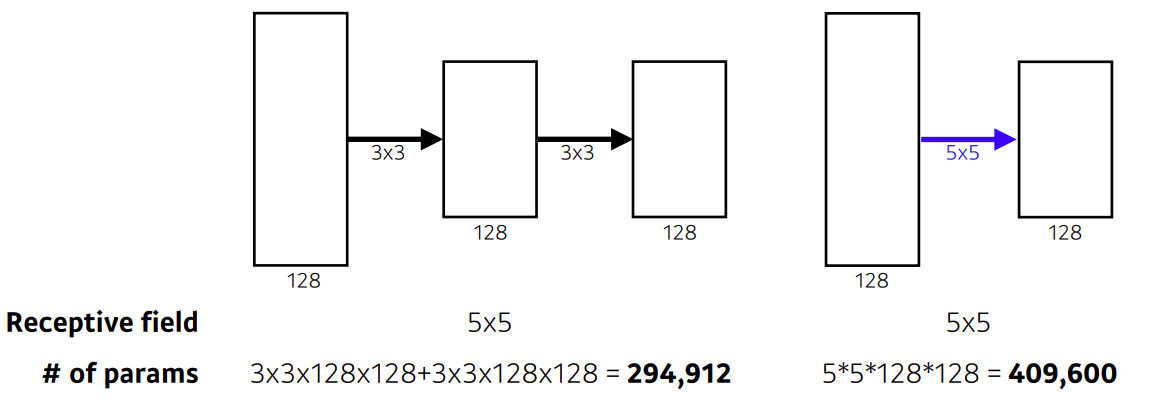
• 같은 receptive field를 얻는 관점에서는 5x5 하나 사용하는 것 보다 3x3 두 개 사용하는게 파라미터 수를 줄인다

GoogLeNet

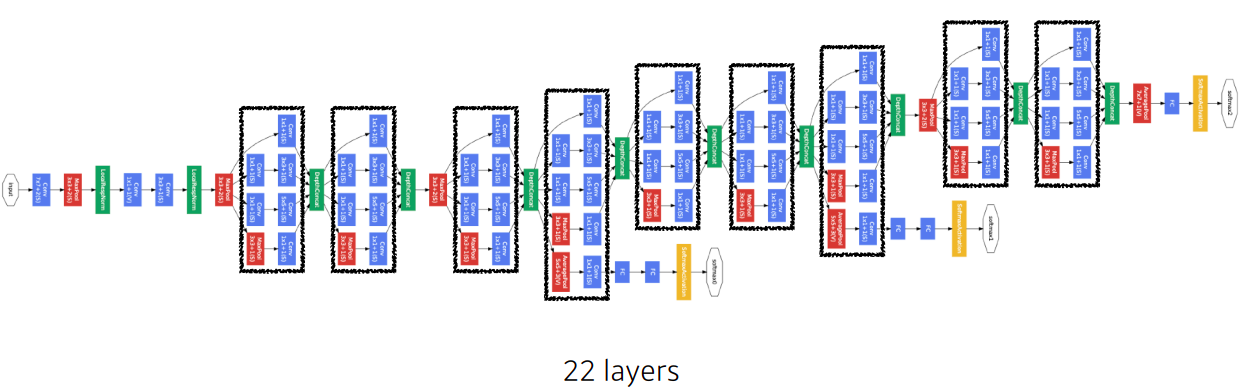
Inception blocks

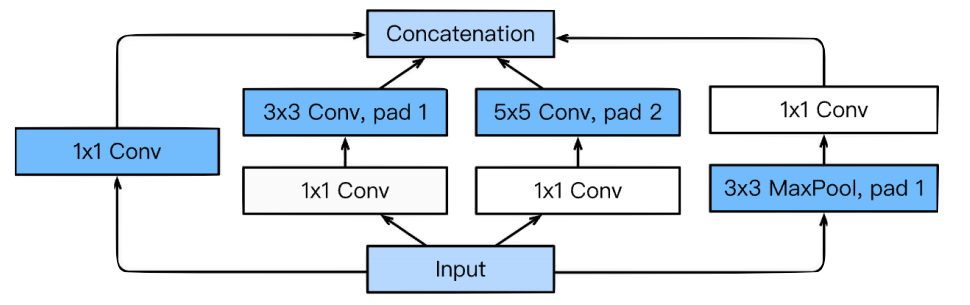
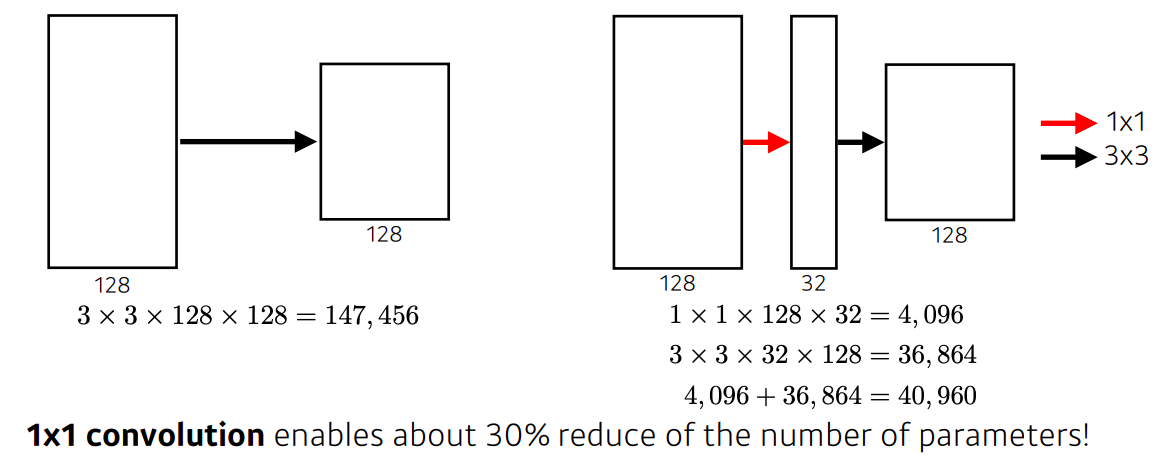
• 3 x 3 과 5 x 5 convolution 하기 전에 1 x 1 convolution의 이점 :
  • 전체적인 네트워크의 파라미터 갯수를 줄인다 (1 x 1 convolution은 채널 방향으로 차원을 줄일 수 있다)
  • how?

Quiz

Which CNN architeture has the least number of parameters?

1) AlexNet(8-layers)

• 60M
  2) VGGNet (19-layers)
• 110M
  3) GoogLeNet (22-layers)
• 4M
• answer is GoogLeNet
• 네트워크 깊이가 더 깊은데 파라미터 숫자를 줄일수 있었던 요인:
  • 뒨단에 있는 dense layer를 줄이고
  • 1 x 1 convolution으로 feature dimension을 줄이기 때문에 이런 효과가 생긴다

ResNet

• 네트워크가 깊어짐에 따라서 학습이 더욱 어려워진다
  • vanishing gradient issue
• ResNet은 이를 해소하기 위해 indentity map (skip connection) 을 추가한다
  • network가 깊을 수록 학습되는 gradient가 noise에 가까워진다
  • (vanishing - shattered gradients) 이를 skip connection을 통해 더 하위 단계에 의미있는 gradient를 전달하게 되어 vanishing gradient 문제 또한 해소
    • 이처럼 학습한다면 layer가 아무리 깊어져도 최소 gradient로 1이상의 값을 가지므로 gradient vanishing 문제를 해결할 수 있게됨

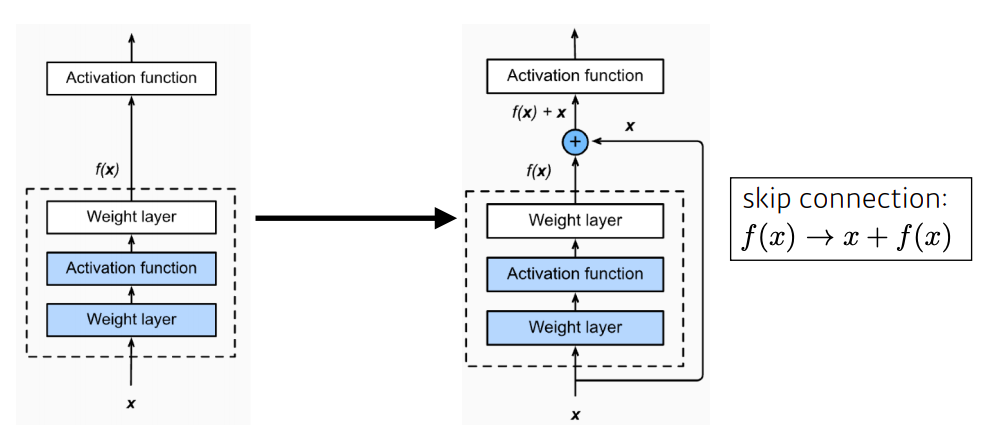
• x를 뉴럴 네트워크의 출력값(한단짜리 convolution layer)에 더한다
• 기존 network 들은 f(x)를 얻기 위해 학습을 했다면, ResNet은 f(x)가 0이 되는 방향으로 학습을 한다
• 그렇다는건 나머지(residual)를 학습한다고 볼 수 있고,
• 그래서 궁극적으로 convolution layer가 학습하고자 하는 quantity는 residual(차이)만 학습한다

Questions

• 단지 gradient vanishing 문제를 해결하기 위해(미분 값이 항상 1이상) skip connection을 쓴건지 아니면 다른 이유가 더 있는건지?

• f(x)가 0에 근접하기 전에(overfitting?) 적절히 epoch 수와 lr을 조절하여 학습을 끊어주는 건가?

• 보통 분류 신경망은 label과 출력값을 cross entropy 함수에 넣어 loss를 계산하는데, loss function이 어떻게 f(x)를 0이 되도록 학습하는건지?

• answer:
  • "단지 gradient vanishing 문제" 라기보단, 이전까지는 층이 깊어질수록 gradient가 vanishing 되는 문제로 인해 학습이 잘 되지 않다
  • 즉 굉장히 중요한 문제다
  • 예를 들면, 100-hidden layers NN 보다, 15-hidden layers NN이 더 좋은 성능을 내고 있었다. 알다시피 층이 깊을수록 더 많은 feature들을 학습하여 좋은 성능을 낼 것으로 기대하는데, 실제는 그렇게 되지 않았다.
  • 보통 우리가 성능을 측정할 때, training과 test의 loss와 accuracy를 보게 되는데, 이 두 개가 서로 상반되는 경우에 우리는 overfitting을 의심하고 (training accuracy는 상승, test accuracy는 하락),
  • 이 두 개가 서로 같은 경향을 띄지만, 전체적인 loss가 크고, accuracy가 낮은 경우에 우리는 vanishing gradient를 의심하게 된다
  • 많은 연구자들이 vanishing gradient를 해결하기 위해 activation function을 바꾸는 등 (sigmoid, tanh, relu,...) 다양한 방법들을 시도해왔는데요, 그 중 효과적인 방법 중 하나가 skip connection이다
  • 하나의 block에만 대해서만 생각하면 f(x) = 0 이 되도록 학습하도록 하는 것에 헷갈릴 것 같은데, 이 f(x) 또한 전체 network의 일부로 cross entropy에 의해 loss가 전달되고 전체 weight들이 update 되게 된다
  • skip connection을 통해, 이전 레이어의 x를 뒷 층으로 보내주고, x의 feature를 그대로 가져가서 residual block의 output과의 차이(= residual)를 대해서 학습할 수 있도록 한다
  • f(x)가 0이 되도록 학습이 되는 것이 맞지만, residual block의 input과 ouput의 차이를 f(x)라고 할 때, 이 차이 (residual)에 조금 더 집중해서 보시면 될 것 같다
  • 예를 들어 resnet에서 plain nn이라 불리는, 기존 nn의 h(x)가 x가 되게 학습한다고 하는데, h(x) 는 결국 예측값 y^을 찾아내는 function 이므로, 결국 우리는 h(x) - y 를 0이 되도록 학습하게 된다
  • 이는 우리가 쉽게 사용하고 있지만, 사실은 굉장히 복잡한 문제인데, x를 어떤 각각의 레이어를 통과시킨 후 나온 결과물인 h(x)가 x에 대한 설명을 잘 하도록 해야 한다
  • 하지만 여러 층의 레이어를 거칠수록 x에 대한 정보가 많이 사라지게 된다
  • 그래서 h(x)를 조금 바꿔 h(x) = f(x) + x 라고 한 후에, 우리가 f(x) 즉, 어떤 레이어를 거치기 전과 후의 차이에 대해서만 집중한다면, 그리고 기존의 input을 그대로 전달해준다면 조금 더 잘 학습되지 않을까? 하는 개념으로 생각하시면 좋을 것 같다
• references
  • 1
  • 2
  • 3
  • 4
  • 5

DenseNet

• DenseNet uses concatenation instead of addition

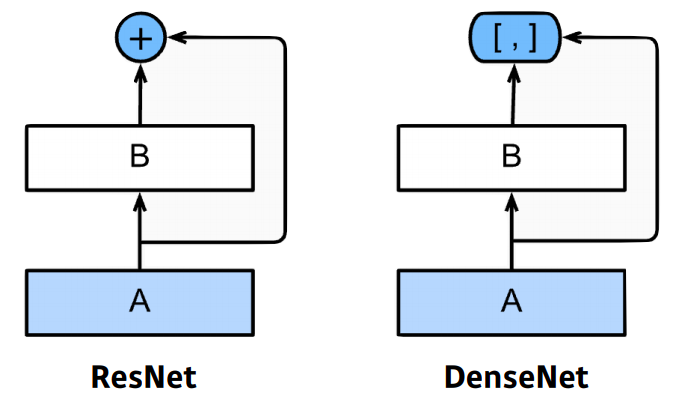
• 문제는 concat 하면 할수록 채널이 커지기 때문에 중간중간에 transition block에서 채널을 줄여주는 1x1 convolution을 넣는다

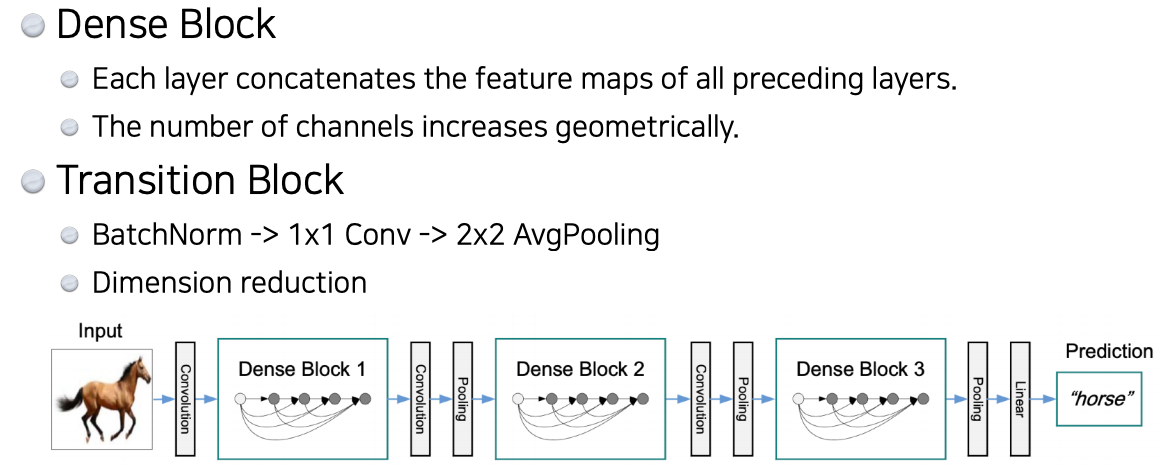
정리

• VGG : repeated 3 x 3 blocks
• GoogLeNet : 1 x 1 convolution
• ResNet : skip - connection
• DenseNet : concatenation

computer vision applications

• semantic segmentation 의 정의, 핵심 아이디어에 대해 설명
• object detection 의 정의, 핵심 아이디어, 추가적으로 종류에 대해 설명

semantic segmentation

• 어떤 이미지가 있을때 이미지의 픽셀마다 분류 하는 technique
  • 자율주행 자동차에서 활용

Fully convolutional network

• Dense layer를 없앤 구조

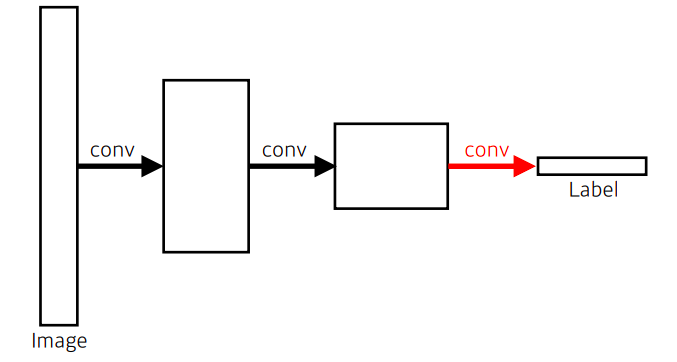
• fully convolutional network는 어떠한 input size(spatial dimension) 로도 작동은 하지만, output dimension(spatial dimension) 역시 줄어든다
• 따라서 spatial resolution이 많이 떨어져있는 output을 원래 모양으로 늘려줘야한다
• 그 방법으로는 Deconvolution (conv transpose) 가 있다

Deconvolution (conv transpose)

• convolution의 역 연산
• spatial dimension을 늘려준다

Detection

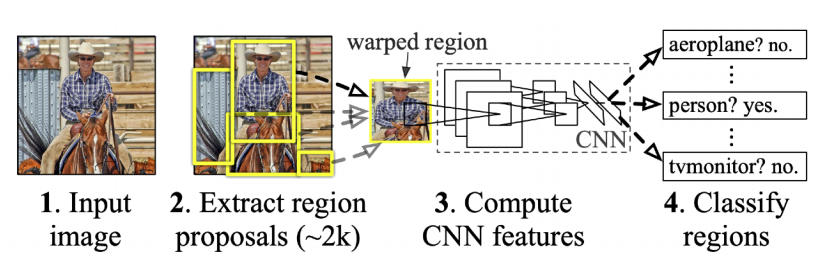
R-CNN

1) takes an input image
2) extracts around 2,000 region proposals (using selective search)
3) compute features for each proposals (using AlexNet)
4) classifies with linear SVMs