[Contents]

1) RNN 첫걸음

RNN 첫걸음

• 시퀀스 데이터의 개념과 특징, 그리고 이를 처리하기 위한 RNN을 소개
• RNN에서의 역전파방법인 BPTT와 기울기 소실문제에 대해 설명
• 시퀀스 데이터만이 가지는 특징과 종류, 다루는 방법, 그리고 이를 위한 RNN(Recurrent Neural Network)의 구조를 앞선 배웠던 CNN이나 다른 MLP(Multi Layer Perceptron)와 비교하면서 공부하자
• RNN에서의 역전파 방법인 BPTT(Back Propagation Through Time)를 수식적으로 이해하고, 여기서 기울기 소실문제가 왜 발생할 수 있는지, 이에 대한 해결책은 어떤 것들이 있는지를 집중

시계열 데이터 (sequence data) 이해하기

• 독립적으로 들어오지 않는 경우가 많다
• 소리, 문자열, 주가 등의 데이터를 sequence 데이터로 분류한다
  • 시계열(time-series) 데이터는 시간 순서에 따라 나열된 데이터로 시퀀스 데이터에 속한다
• 시퀀스 데이터는 독립동등분포(independent identical distribution) 가정을 잘 위배하기 때문에 순서를 바꾸거나 과거 정보에 손실이 발생하면 데이터의 확률분포도 바뀌게 된다
  • 과거 정보 또는 앞뒤 맥락 없이 미래를 예측하거나 문장을 완성하는 건 불가능 하다

시퀀스 데이터를 어떻게 다루나요?

• 이전 시퀀스의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위해 조건부확률을 이용할 수 있다
  • 이전에 배운 베이즈 법칙을 사용
  • $P(X_1, ..., X_t) = P(X_t|X_1, ..., X_{t-1})P(X_1, ..., X_{t-1}) = P(X_t|X_1, ..., X_{t-1})P(X_{t-1}| X_1, ..., X_{t-2})$ x $P(X_1,...,X_{t-2}) = \prod_{s=1}^t P(X_s|X_{s-1}, ..., X_1)$
    • $\prod$ : 이 기호는 s= 1, ..., t 까지 모두 곱하라는 기호이다
  • $X_t \sim P(X_t|X_{t-1}, ..., X_1)$
    • 위 조건부확률은 과거의 모든 정보를 사용하지만 시퀀스 데이터를 분석할 때 모든 과거 정보들이 필요한 것은 아니다
• 시퀀스 데이터를 다루기 위해선 길이가 가변적인 데이터를 다룰 수 있는 모델이 필요하다
  • $X_t \sim P(X_t|X_{t-1}, ..., X_1)$
  • $X_{t-1} \sim P(X_{t+1}|X_t,X_{t-1}, ..., X_1)$
    • 조건부에 들어가는 데이터 길이는 가변적이다(변동이 가능하다)
• 꼭 과거에 모든 정보를 가지고 예측을 할 필요는 없기 때문에 만약에 현재 시점에서 봤을때 최근 몇년간의 데이터 또는 앞서 몇개의 문장만 보고서도 충분히 모델링이 가능한 문제의 경우에는 초기시점에서 모든 정보를 다 사용할 필요없이 고정된 길이 $\tau$ 만큼의 시퀀스만 사용을 해서 예측을 할때 이용이 가능하다.
  • 이런경우에는 가변적인 길이가 아니라 $\tau$ 라는 고정된 길이를 사용하는 모델이 된다
  • 고정된 길이 $\tau$ 만큼의 시퀀스만 사용하는 경우 AR($\tau$) (Autoregressive Model) 자기회귀모델이라고 부른다
  • $X_t \sim P(X_t|X_{t-1}, ..., X_{t-\tau})$
  • $X_{t-1} \sim P(X_{t+1}|X_t,...,X_{t-\tau+1})$
    
• 경우에 따라서 먼 과거의 정보들도 필요할때가 있다
  • 이런경우 사용되는 방법이 latent autoregressive model(잠재 자기회귀 모델) 이다
  • latent autoregressive model : 바로 직전과거의 정보는 $X_{t-1}$로 묶고 그 훨씬이전의 정보들을 $H_t$라고 해서 잠재 변수로 인코딩을 한다
  • 그러면 $X_t$를 예측을 할 때는 $X_1$ 에서 부터 $X_{t-2}$ 까지의 정보를 가지고 $H_t$ 라는 잠재변수를 만들게 되고
  • $X_{t+1}$ 에서는 $X_1$에서 부터 $X_{t-1}$ 까지의 정보를 가지고 $H_{t+1}$ 이라는 잠재변수를 만든다
  • 이렇게 되는 경우에는 바로 이전 직전 정보랑 잠재변수 이 두가지 데이터만 가지고 미래 시점을 예측을 할 수 있기 때문에 이제 부터는 가변적이지 않고 고정된 길이에 데이터를 가지고 모델링이 가능하다
  • 장점 : 과거 모든 데이터를 가지고 예측을 할 수 있고 또한 가변적인 데이터의 문제를 고정된 데이터의 길이고 바꿀 수 있다
  • $X_t \sim P(X_t|X_{t-1}, H_t)$
  • $X_{t-1} \sim P(X_{t+1}|X_t,H_{t+1})$
    • $H_t = Net_\theta(H_{t-1}, X_{t-1})$
    • 잠재변수 $H_t$ 를 신경망을 통해 반복해서 사용하여 시퀀스 데이터의 패턴을 학습하는 모델이 RNN이다

RNN(Recurrent Neural Network) 이해하기

• 가장 기본적인 RNN 모형은 MLP와 유사한 모양이다

  • $O_t = H_tW^{(2)} + b^{(2)}$
  • $H_t = \sigma(X_tW^{(1)} + b^{(1)})$
  • $X_t \rightarrow H_t \rightarrow O_t$
  • $H$ : 잠재변수, $\sigma$ : 활성화함수, $W$ : 가중치행렬, $b$ : bias
    • $W^{(1)}, W^{(2)}$ 는 시퀀스와 상관없이 불변인 행렬이다
    • 입력데이터가 t 번째만 들어오기 때문에 이 모델은 과거의 정보를 다룰 수 없고 오로지 현재 시점의 데이터만 가지고 예측을 한다

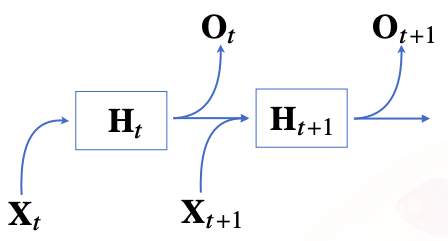
• RNN은 이전 순서의 잠재변수와 현재의 입력을 활용하여 모델링 한다

  • $O_t = H_tW^{(2)} + b^{(2)}$
  • $H_t = \sigma(X_tW_X^{(1)} + H_{t-1}W_H^{(1)} + b^{(1)})$
  • 잠재변수인 $H_t$를 복제해서 다음 순서의 잠재변수를 인코딩하는데 사용
    

• RNN의 역전파는 잠재변수의 연결그래프에 따라 순차적으로 계산한다

  • 이를 Backpropagation Through Time (BPTT) 이라 하며 RNN의 역전파 방법이다

  • 잠재 변수에 들어오는 gradient는 2가지이다
    1) 다음 시점에서의 잠재변수에서 들어오게되는 gradient vector
    2) 출력에서 들어오게되는 gradient vector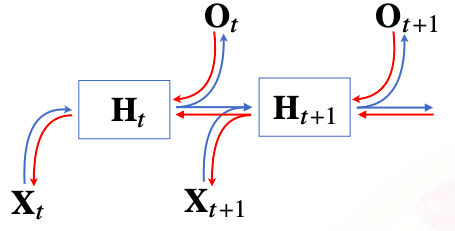

    

BPTT 를 좀 더 살펴보자

• BPTT를 통해 RNN의 가중치행렬의 미분을 계산해보면 아래와 같이 미분의 곱으로 이루어진 항이 계산된다
  
• 시퀀스 길이가 길어질수록 즉, 현재시점부터 예측이 끝나는 $T$ 시점까지 시퀀스가 길어질 수록 곱해지는 항들이 불안정해지기 쉽다
  • 만약 이값이 1보다 크게되면 굉장히 크게 커지게 되고
  • 만약 이 값이 1보다 작게되면 굉장히 작은 값으로 떨어지기 때문에 미분값이 엄청 커지거나 또는 미분값이 엄청 작아지게 될 확률이 높다
  • 그렇게 때문에 일반적인 BPTT를 모든 $t$ 시점에 적용하면 RNN의 학습이 불안정해지기 쉽다

기울기 소실의 해결책?

• 가장 주의해야할 점은 gradient 가 0으로 줄어드는 즉 gradient 가 vanishing (기울기 소실) 하는 현상이 굉장히 큰 문제가 된다

  • 앞선 미래 시점에 가까울수록 gradient가 살아있고 과거 시점으로 갈수록 gradient가 점점 0으로 가게 되면 과거 정보를 유실할 확률이 높다

• 시퀀스 길이가 길어지는 경우 BPTT를 통한 역전파 알고리즘의 계산이 불안정 해지므로 길이를 끊는 것이 필요하다

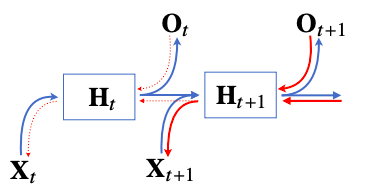
  • 이를 truncated BPTT라 부른다
    

• 이런 문제들 ㄸ문에 Vanilla(기본적인) RNN은 길이가 긴 시퀀스를 처리하는데 문제가 있다

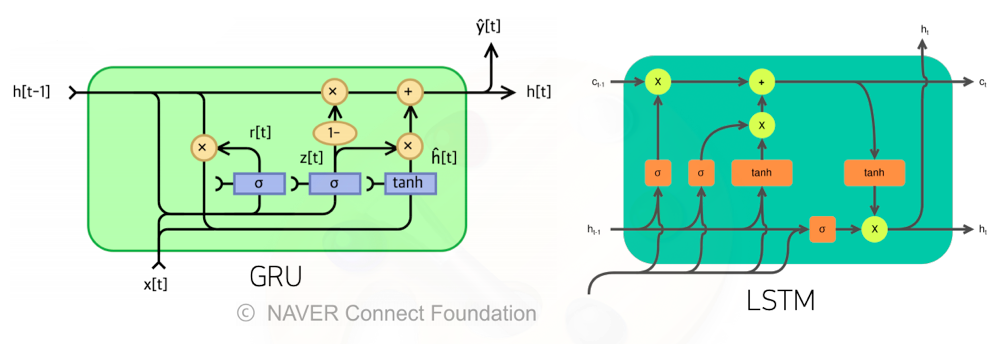
  • 이를 해결하기 위해 등장한 RNN 네트워크가 LSTM과 GRU이다