[Contents]

1) Generative Models part 1
2) Generative Models part 2

Generative Models part 1

• 머신러닝, 딥러닝에서 의미하는 Generative model이 무엇인지, 이해하기 위한 기본적인 통계 이론, 다양한 Generative model의 수식아이디어, 구조에 대해 설명

What Generative Models can do

• 강아지 사진들이 주어졌을때
• 다음과 같은 확률 분포 $p(x)$를 배우고 싶다
  • generation : if we sample $x_{new} \sim p(x), x_{new}$ should look like a dog(sampling)
    • 학습데이터에 있지 않은 강아지와 같은 이미지를 만들어낼 수 있다
  • density estimation : $p(x)$ should be high if $x$ looks like a dog, and low otherwise (anomaly detection)
    • 어떤 이미지가 들어왔을때 이 이미지가 강아지 같을수록 확률값이 높다
    • 마치 분류 모델같다. Also known as, explicit model
      • explicit model : 어떤 입력이 주어졌을때 이 입력에 대한 확률값을 얻어낼수 있는 모델
      • implicit model : 단순히 generate 만 하는 모델
    • 따라서 엄밀히 말하면 generative model은 분류모델을 포함하고 있다
  • unsupervised representation learning : we should be able to learn what these images have in common, e.g., ears, tail, etc (feature learning)
• 그렇다면, $p(x)$ 는 어떻게 만들수 있을까?
  • 이를 알기 위해선 확률의 아주 간단한 기본 지식이 필요하다

Basic Discrete Distributions

• Bernoulli distribution(베르누이) :
  • $D$ = {Heads, Tails}
  • specify $P(X=Heads) = p$, then $P(X=Tails)= 1-p$
  • 확률론과 통계학에서 매 시행마다 오직 두 가지의 가능한 결과만 일어난다고 할 때,
  • 각 시행에서 성공의 결과가 나타날 확률은 $p=P(S)$로 나타내며, 실패가 나타날 확률을 $q=P(F)=1-p$로 나타낸다
  • 그리고 $p+q=1$이 된다
• Categorical distribution :
  • $D$ = {1,...,m}
  • specify $P(Y = i) = p_i$ such that $\sum_{i=1}^m p_i = 1$
  • 예) 6개의 주사위를 던지는데 몇개의 parameter가 필요할까?
    • n-1 즉 5개의 parameter가 필요하다
    • 왜냐하면 나머지 5개의 파라미터가 있으면 마지막 하나는 1에서 다 빼주면 된다
• example
  • modeling an RGB joint distribution (of a single pixel)
    • $(r,g,b) \sim p(R,G,B)$
    • number of cases?
      • 256 x 256 x 256
    • how many parameters do we need to specify?
      • 255 x 255 x 255
      • 하나의 RGB 픽셀을 fully describe 하기위해서 필요한 파라미터의 숫자는 엄청 많다
• example 2
  • suppose we have $X_1, ..., X_n$ of n binary pixels (a binary image)
  • how many possible states? (경우의 수)
    • 2 x 2 x ... x 2 = $2^n$
  • how many parameters to specify $p(x_1, ..., x_n)$?
    • $2^n$ - 1
• 파라미터의 숫자가 많을수록 학습은 어렵기 때문에 파라미터의 숫자를 줄이기 위해 n개의 픽셀들이 모두 독릭접이라고 가정해본다
• 파라미터 : 확률을 표현하는데 필요한 변수의 갯수

Structure Through Independence

• n 개의 픽셀이 독립적이라면
  • possible state(경우의 수)는 $2^n$ 으로 같다
    • 모든 픽셀이 0 또는 1을 가질 수 있기 때문에 n개의 픽셀이면 $2^n$이다
  • distribution을 표현하기 위해서 필요한 파라미터의 수는 n 개만 있으면 된다
    • 각각의 픽셀에 대해서 파라미터 한개만 있으면 되고 n개가 모두 독립적으로 있기 때문에 다 더하기만 하면 된다
• $2^n$ entries can be described by just n numbers. But this independence assumption is too strong to model useful distributions

Conditional Independence

• fully dependent하면 너무 많은 파라미터가 필요하고
• 이를 독립적으로 가정하면 파라미터의 숫자가 많이 줄어들어서 좋은데 표현할수 있는 이미지가 너무 적다
• 그렇기 때문에 중간지점을 타협하기 위해 3가지 중요한 규칙이 필요하다
• Three important rules
  • Chain rule :
    • $p(x_1, ..., x_n) = p(x_1)p(x_2|x_1)p(x_3|x_1,x_2) ... p(x_n|x_1, ..., x_{n-1})$
  • Bayes' Rule :
    • $p(x|y) =$ $p(x,y) \over p(y)$ = $p(y|x)p(x) \over p(y)$
  • conditional independence :
    if $x \bot y | z$ , then $p(x|y, z) = p(x|z)$
    • z 가 주어졌을때 x 와 y 가 독립적이다
    • x and y are conditionally indepedent when given z
  • conditional indepedence 와 chain rule을 섞어서 fully depedence 모델과 fully independent 모델 사이의 타협되는 모델을 만든다
• markov assumption
  • $p(x_1, ..., x_n) = p(x_1)p(x_2|x_1)p(x_3|x_2) ... p(x_n|x_{n-1})$
  • how many parameters?
    • 2n - 1
  • hence, by leveraging the Markov assumption, we get exponential reduction on the # of parameters
  • Auto-regressive model leverage this conditional independency

Auto-regressive model

• suppose we have 28 x 28 binary pixels
• our goal is to learn $p(x) = p(x_1, ..., x_{784})$ over $x \in$ {0, 1}$^{784}$
• how can we parametrize $p(x)$?
  • let's use the chain rule to factor the joint distribution
  • $p(x_{1:784}) = p(x_1)p(x_2|x_1)p(x_3|x_{1:2})...$
  • this is called an autoregressive model
    • autoregressive model 은 어떤 하나의 정보가 이전 정보들의 dependent하다는걸 말한다
    • markov assumption 을 통해서 i번째 픽셀이 i-1 번째 픽셀에만 dependent 한것도 autoregressive 모델 이지만
    • i 번째 픽셀이 1부터 i-1번째 픽셀에 모든 정보들에 dependent 한것도 autoregressive model이다
  • note that we need an ordering of all random variables
    • 순서를 매겨야하기 때문이다
    • 이미지에 순서를 매긴다는 것은 명확하지 않다 왜냐하면 이미지는 2차원 공간인데 순서는 1차원 줄이기 때문이다
    • 그렇기 때문에 이미지는 다양한 방법으로 순서를 매길수가 있다
    • 그리고 순서를 매기는 방법에 따라서 성능이 달라질 수가 있다

NADE : Neural Autoregressive Density Estimator

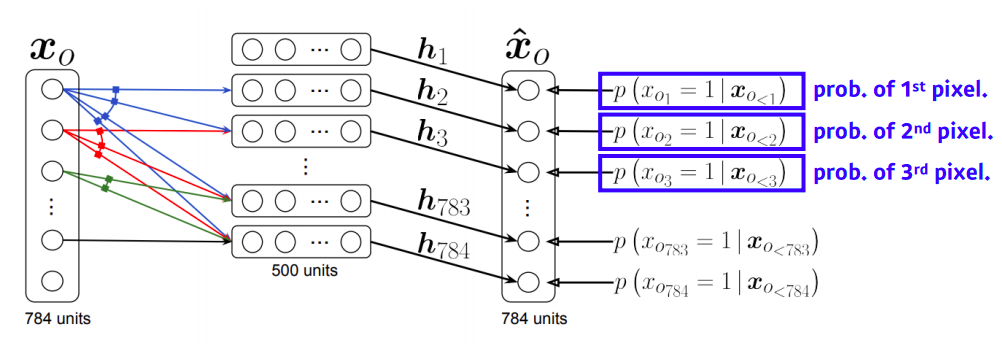
• the probability distribution of i-th pixel is
  • $p(x_i|x_{1:i-1}) = \sigma(\alpha_ih_i + b_i)$ where $h_i = \sigma(W_{<i}x_{1:i-1} + c)$
• i번째 픽셀을 첫번째부터 i-1번째 픽셀에 dependent 하게 한다
• neural network 입장에서는 입력차원이 계속 변한다
  • 그래서 weight가 계속 커진다
  • 즉 3번째 픽셀에 대한 확률분포를 만들때는 1번째와 2번째 총 2개의 입력을 받는 weight가 필요한 반면
  • 100번째 필섹에 대한 확률분포를 만들때는 99개의 입력을 받는 weight가 필요하다
• NADE is an explicit model that can compute the density of the given inputs
  • 단순히 generate만할 수 있는 것이 아니라 임의의 784개의 binary vector가 주어지면 이에 대한 확률을 계산할 수 있다
• how can we compute the density of the given images?
  • suppose we have a binary image with 784 binary pixels, {$x_1, x_2, ..., x_{784}$}
  • then, the joint probability is computed by
    • $p(x_1, ..., x_{784}) = p(x)p(x_2|x_1)...p(x_{784}|x_{1:783})$
    • where each conditional probability $p(x_i|x_{1:i-1})$ is computed independently
• In case of modeling continuous random variables, a mixture of Gaussian can be used

pixel RNN

• we can also use RNNS to define an auto-regressive model
• for example, for an n x n RGB images,
  • $p(x) = \prod_{i=1}^{n^2}p(x_{i,R}|x_{<i})p(x_{i,G}|x_{<i},x_{i,R})p(x_{i,B}|x_{<i},x_{i,R},x_{i,G})$
  • $p(x_{i,R}|x_{<i})$ : Prob. i-th R
  • $p(x_{i,G}|x_{<i},x_{i,R})$ : Prob. i-th G
  • $p(x_{i,B}|x_{<i},x_{i,R},x_{i,G})$ : Prob. i-th B
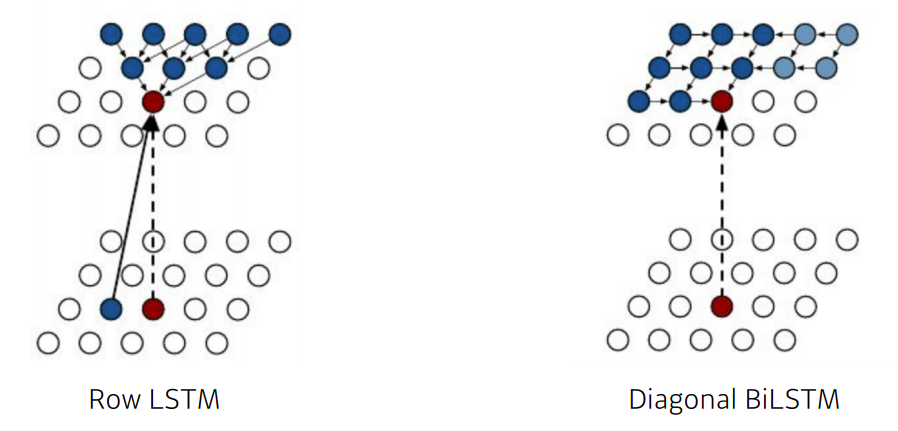
• There are two model architectures in Pixel RNN based on the ordering of chain:
  • Row LSTM : i번째 픽셀을 만들때 위쪽에 있는 정보를 활용
  • Diagonal BiLSTM : bidirectional LSTM을 활용하되 자기 이전 정보들을 다 활용

Key Takeaways

• Generative model은 단순히 무언가를 생성하는 implicit model 뿐만 아니라 입력에 대한 확률값을 출력하는 explicit model도 있다
• 파라미터 숫자를 통해서 fully independent model, fully dependent model 그리고 conditional independence + chain rule을 활용해서 auto-regressive model 을 알아봤다

Generative Models part 2

• Generative models part 2 에서는 실제로 많이 다뤄지는 Practical 한 Generative model인 Variational Auto Encoder와 Generative Adversarial Network 를 이용하여 Latent variable model 에 대해 설명

Further Reading

• 1시간 만에 GAN 완전 정복하기
• An Intro to Variational Autoencoders(저자)