Image classification 2

• 이번에는 Image Classification 1 에 이어서 대표적인 CNN 모델들에 대해 배운다
• 먼저 VGGNet과 비슷한 시기에 등장한 GoogLeNet을 시작으로, 지금도 많이 쓰이고 있는 ResNet에 공부하고 실습을 진행한다
• 이 외에도 추가적으로 몇가지 CNN 모델들에 대한 소개를 한다
• AlexNet, VGGNet, GoogLeNet, ResNet 에 대하여 메모리 측면과 계산 효율 관점에서 비교 분석 한다

Further Reading

• ResNet

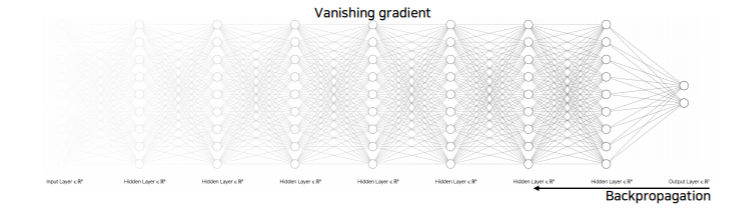
Problems with deeper layers

Going deeper with convolutions

• The neural network is getting deeper and wider
  • Deeper networks learn more powerful features, because of
    • Larger receptive fields
      • 더 많은 주변을 참조해서 신중히 결론을 내린다
    • More capacity and non-linearity
• But, does getting deeper and deeper always work better?

Hard to optimize

• Deeper networks are harder to optimize
  • Gradient vanishing/exploding
  • computationally complex
  • degradation problem
    

CNN architectures for image classification 2

GoogLeNet

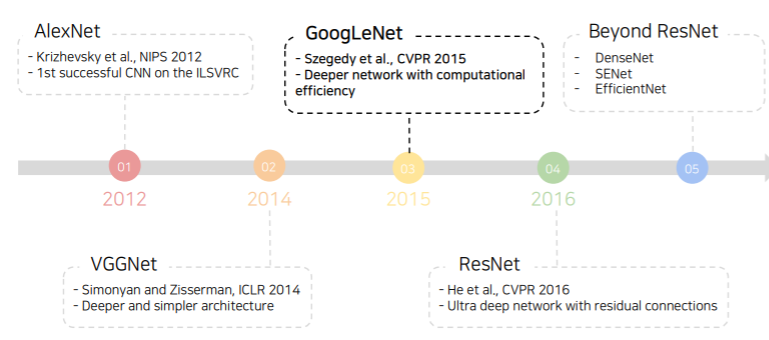
• Inception module
  • Apply multiple filter operations on input activation from the previous layer:
  • 하나의 layer에서 다양한 크기의 convolution filter를 사용해서 여러 측면으로 activation을 관찰한다는 의미 (depth가 아닌 width 확장)
    • 1x1, 3x3, 5x5 convolution filters
    • 3x3 pooling operation
  • Concatenate all filter outputs together along the channel axis
  • 한층에 여러 filter를 많이 사용하게 되면 계산 복잡도와 용량이 매우 커진다
  • The increased network size increases the use of computational resources
    • Use 1x1 convolutions
      
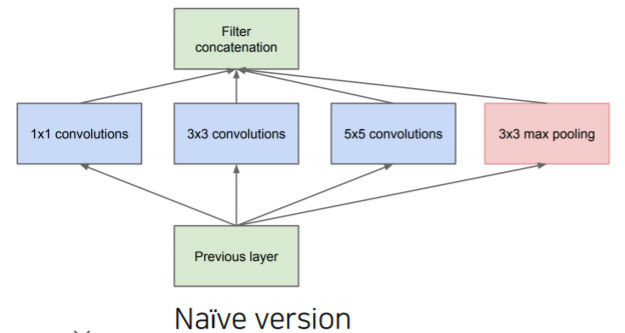
• Use 1x1 convolutions as 'bottleneck' layers that reduce the number of channels
  • 다른 크기의 convolution을 적용하기 전에 channel dimension을 1x1 convolutions을 통해서 줄여주고
  • 압축된 activation map 상에서 계산이 좀 더 복잡한 3x3, 5x5 convoultion filter를 적용할 때 이전보다 계산이 훨신 쉬워진다
  • 3x3 max pooling 에서도 1x1 convolution을 통해서 channel dimension을 바꾸준다
    
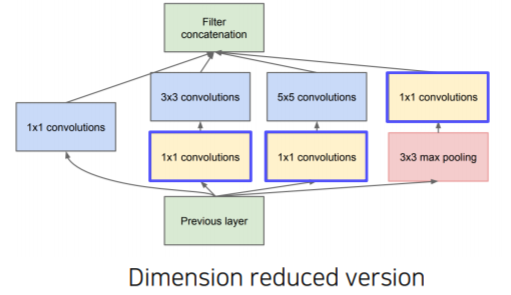
• 1x1 convolutions
  • Activation map 상에서 각 픽셀 위치에 해당하는 channel 축으로 값을들 쌓으면 하나에 벡터가 형성이 된다
  • 이 벡터와 1x1 filter 벡터와 내적을 한다
  • 위 과정을 slide window 방식으로 돌아가면서 계산을해서 filter 된 activation map을 생성하게 된다
  • 위처럼 m개의 filter를 사용하여 내적을 통해 m개의 channel dimension으로 줄여주게 된다
    
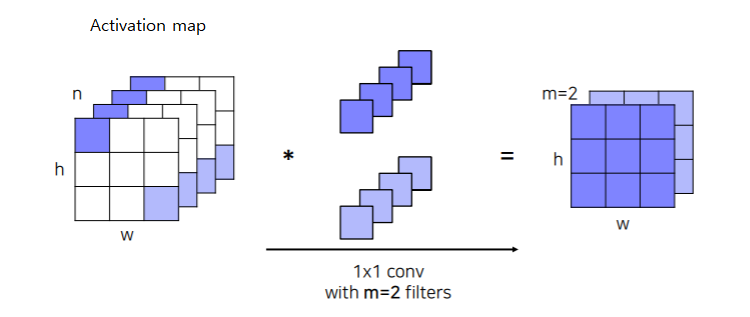
  • 1x1 convolution 계산을 하게되면 공간 크기는 변하지 않지만 각 픽셀 독립적으로 채널 수 만 바꿔주는 걸로 생각하자

overall architecture

• Stem network: vanilla convolution networks
  
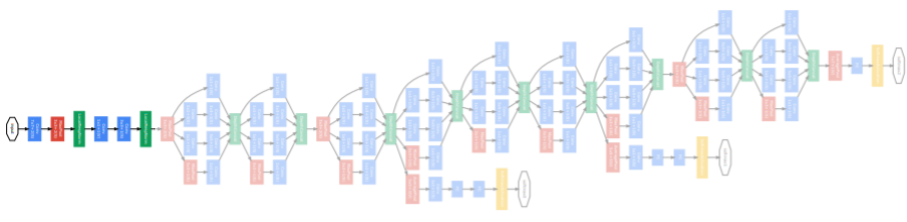
• stacked inception modules
  
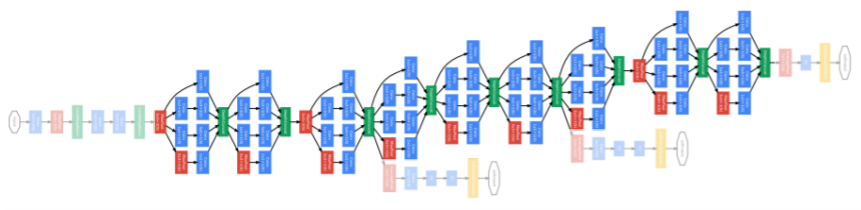
• auxiliary classifiers
  • gradient vanishing/exploding을 막기위해 gradient를 중간중간에 주입해준다
    
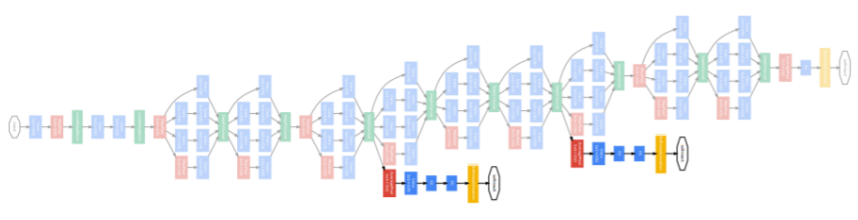
• Classifier output (a single FC layer)
  

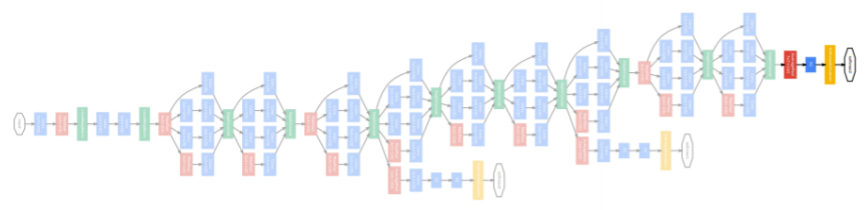
Auxiliary classifier

• The vanishing gradient problem is dealt with by the auxiliary classifier
• Injecting additional gradients into lower layers
• Used only during training, removed at testing time
  

ResNet

• Top-5 validation error on the ImageNet
  • 최초로 100개의 layer가 넘게 적층하면서 더 깊은 layer 를 쌓을수록 성능이 높아진다는 것을 보여준 첫 논문
    
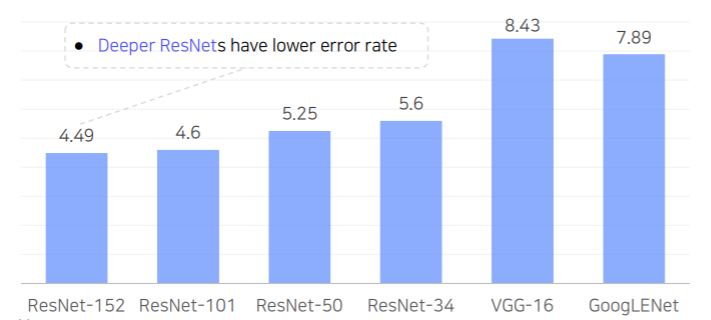
• Revolutions of depth
  • Building ultra-deeper than any other networks
  • What makes it hard to build a very deep architecture?
    - degradation problem
    
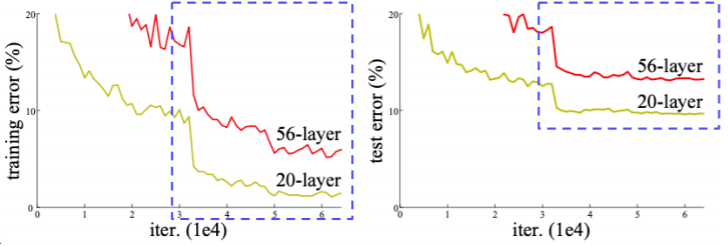
• Degradation problem
  • As the network depth increases, accuracy gets saturated ⇒ degrade rapidly
  • This is not caused by overfitting. The problem is optimization
    • 만약 오버피팅 문제였다면 56 layer의 training과 test error 가 20 layer의 training과 test error 보다 작았을 것이다
    • 이는 최적화의 문제로 인해서 56 layer 모델이 학습이 잘 안된것이다
      • 최적화 문제 : gradient exploding/vanishing

• Hypothesis
  • Plain layer: As the layers get deeper, it is hard to learn good $H(x)$ directly
    • $H(x)$라는 mapping을 학습할때 layer을 높게 쌓아서 곧바로 $x$ 에서 부터 $H(x)$의 관계를 학습하려고 하면 복잡하기 때문에 학습하기가 어렵다
  • Residual Block: instead, we learn residual
    • 현재 주어진 identity외에 나머지 잔여 부분(residual block)만 모델링을 해서 학습을 하게끔 하면 학습의 부담을 경감할 수 있다고 제안
    • Target function : $H(x) = F(x) + x$
    • Residual function : $F(x) = H(x) - x$
    • identity 부분을 남겨놓고 residual 부분만 합성을 해서 $H(x)$라는 새로운 target function을 합성한다
    • 이 $H(x)$ 가 복잡할때 적어도 자기 자신을 보존하는 노력은 하지 않아도 된다고 explicit하게 모델링을 해준다
    • 이것을 구현하기 위해서 해결책으로 shortcut(skip) connection을 제안
• A solution: Shortcut connection
  • Use layers to fit a residual mapping instead of directly fitting a desired underlying mapping
  • The vanishing gradient problem is solved by shortcut connection
    • backprogation 과정 중 identity 부분을 제외한 다른 부분의 gradient가 vanishing 되더라도 적어도 identity 부분에서는 gradient가 flowing 되게 때문에 학습 가능한 chance를 얻을 수 있다
  • Don’t just stack layers up, instead use shortcut connection!
    
• Analysis of residual connection
  • During training, gradients are mainly from relatively shorter paths
  • Residual networks have $O(2^n)$ implicit paths connecting input and output, and adding a block doubles the number of paths
    
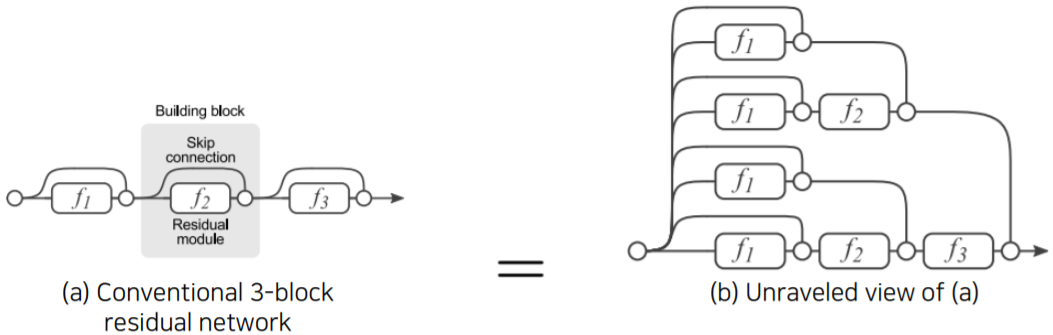
  • 따라서 residual connection이 $2^n$ 으로 gradient가 지나갈 수 있는 input/output path 를 생성한다
  • residual block을 하나 추가할 때마다 경로 수가 2배씩 늘어난다
  • 따라서 gradient가 출력단에서 부터 입력단 까지 바로 가는 path 에서 부터 중간을 모두 거쳐가는 path 까지 다양한 경로를 통해서 굉장히 복잡한 mapping을 학습 해낼 수 있다

Overall architecture

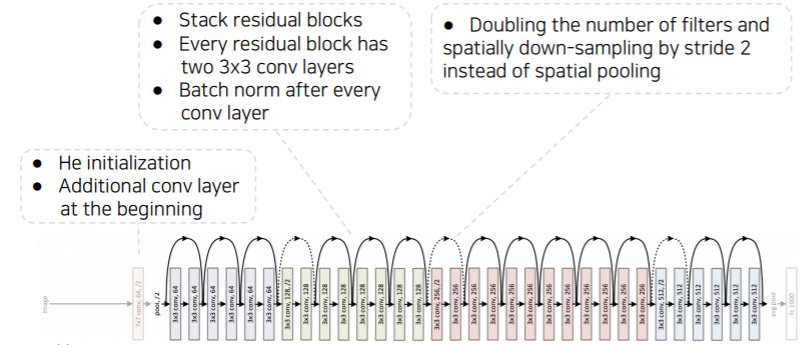
• He initialization로 시작
  • identity conection 즉, 더하기 operation일때 일반적인 initialization을 사용하면 시작부터 더해진 값이 굉장히 큰 값이 되고 계속 큰 값이 더해져서 너무 커지게 된다
  • 따라서 이런 부분을 고려해서 residual connection에 적합한 initialization 방법인 He initialization 을 사용한다
• 색깔 별로 convolution block들이 나눠져 있다
  • 한 block을 넘어갈 때마다 공간적으로는 절반으로 줄면서 채널 수는 2배씩 늘어난다

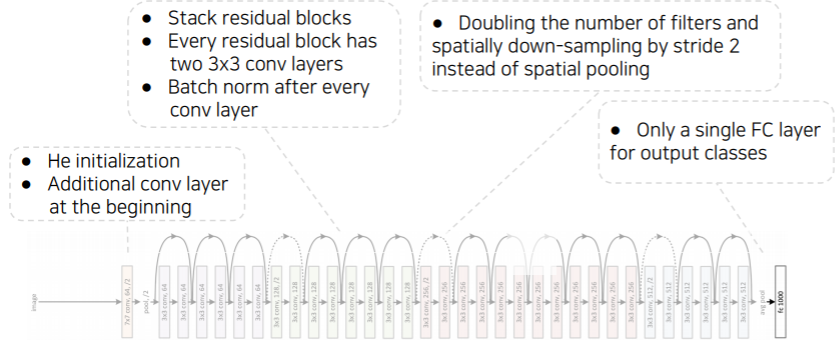
pytorch code for ResNet

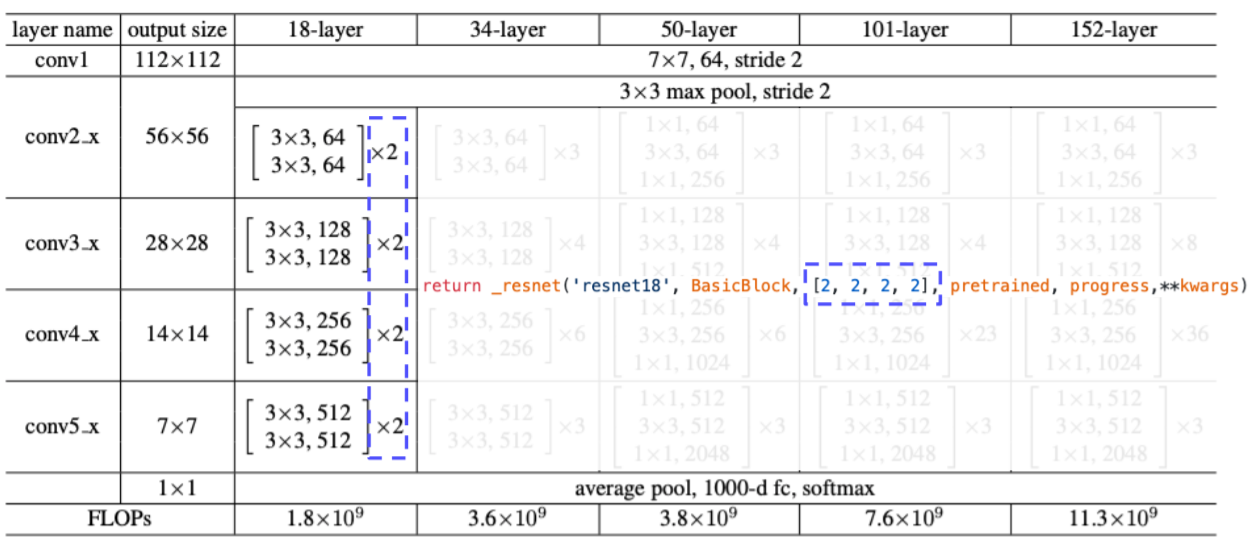
• ResNet 18기준으로 다음과 같이 하이퍼 파라미터를 넣는다

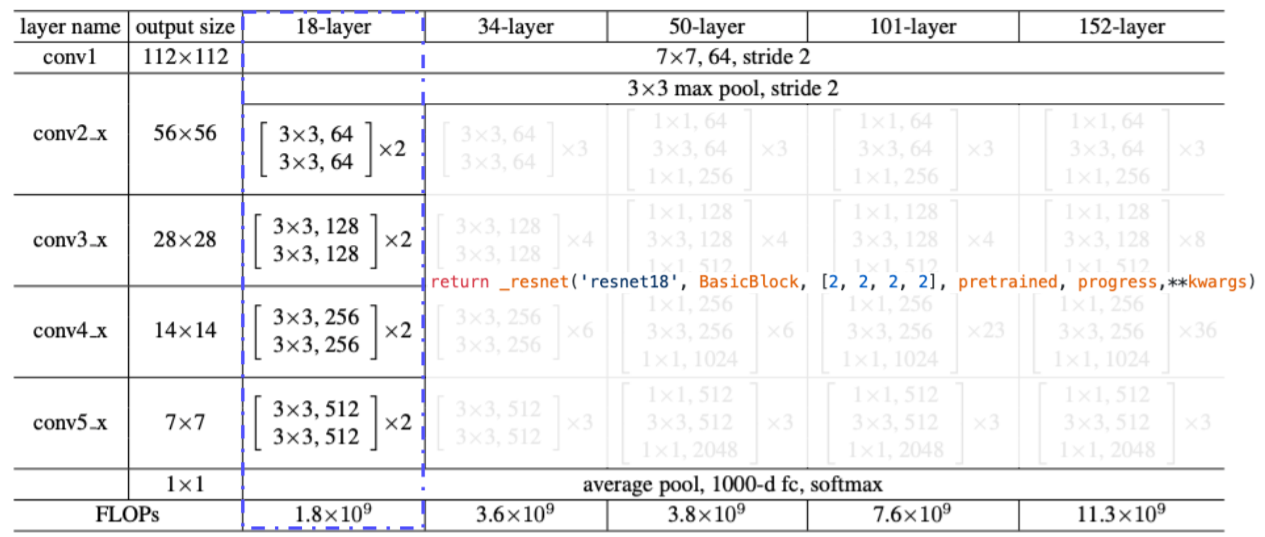
• 여기서 하이퍼 하라미터는 resnet 기본 블록을 쓸것인지를 basic block으로 정해준다
• 각 convolution block 계층 내에 몇개의 block을 쌓을건지 리스트로 받는다
  • 여기서는 4개의 convolution 계층에 2개의 block을 받게 된다

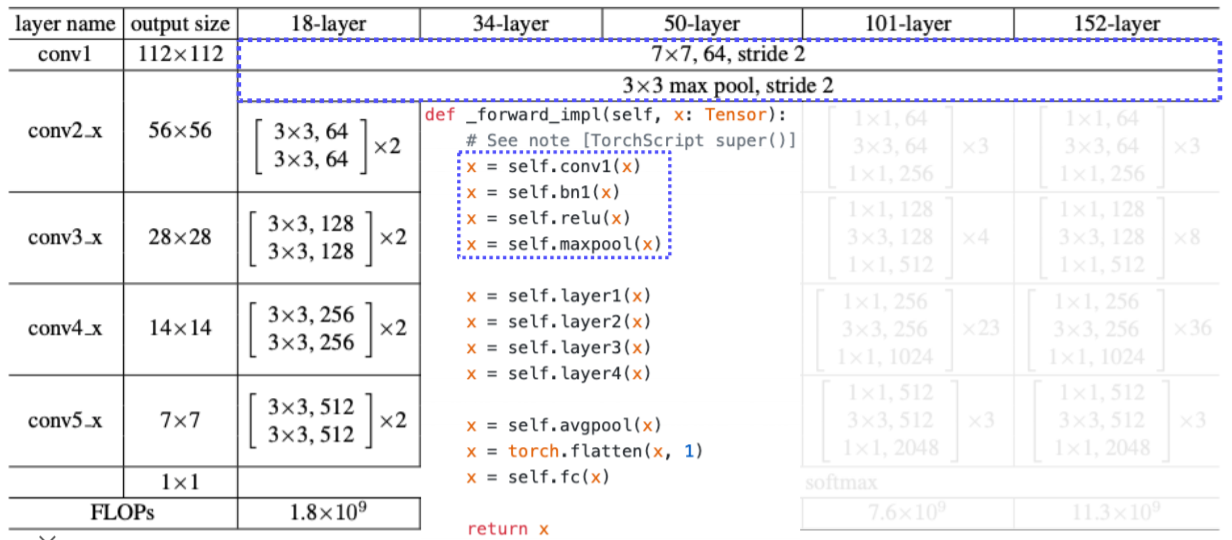
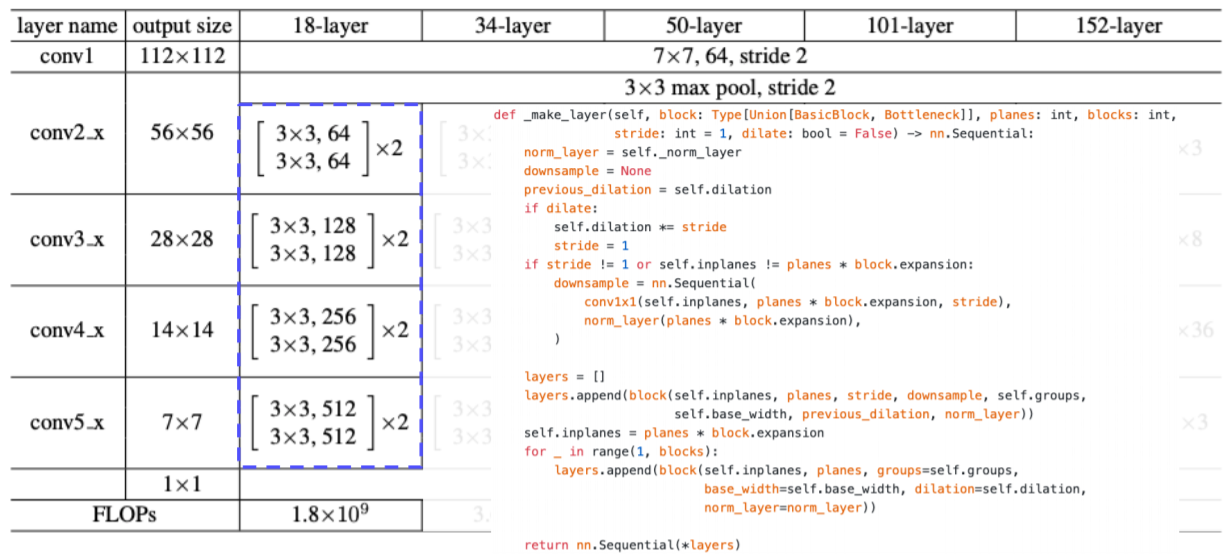
• layer 라는 함수는 conv. block 자체를 형성하게 된다
• layer 는 make_layer 라는 여러가지 연산들을 포함한 함수로 구현
• 파라미터에 맞춘 conv. block을 생성해준다
• layer가 깊어짐에 따라 점점 채널 수가 2배씩 증가하고 stride 가 일정하게 2로 들어가 있으므로 공간축이 2씩 나눠져서 두배씩 줄어든다

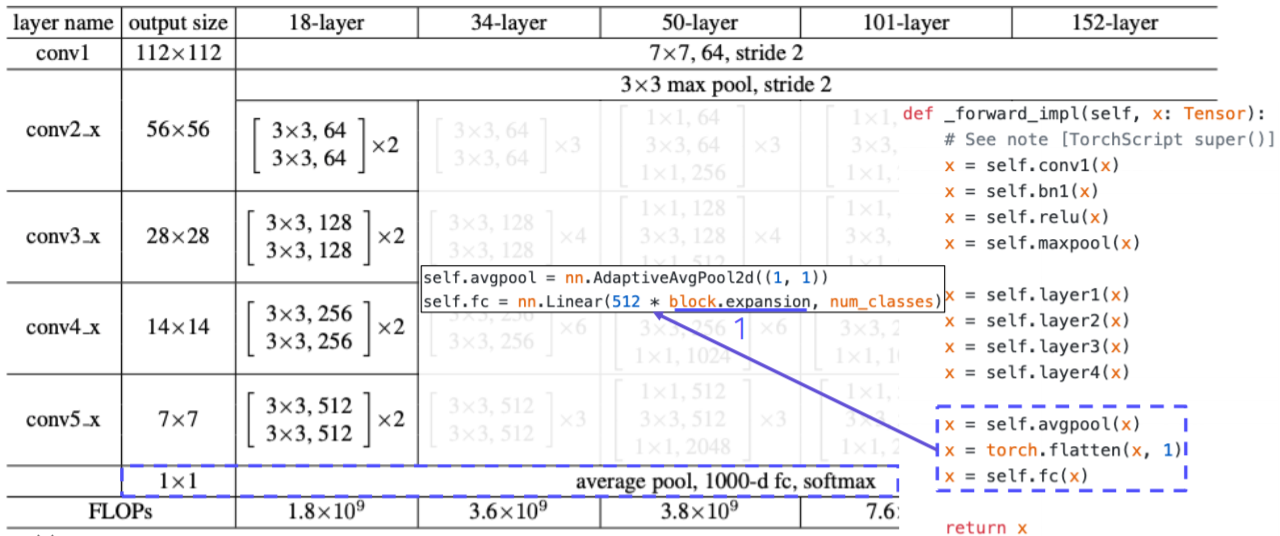
• conv layer들을 모두 거친 결과를 global average pooling을 통해서 벡터화한 후에 하나의 fc(linear) layer 을 통과 시켜서 logit 값을 출력한다

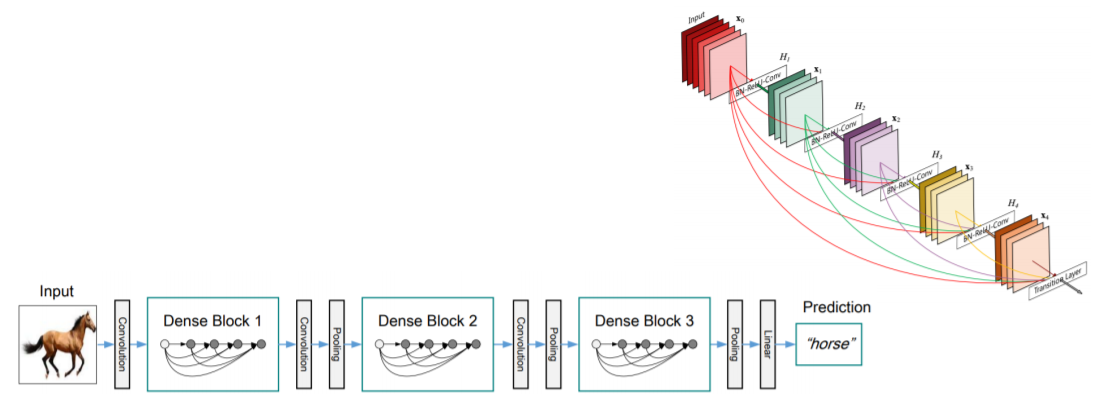
DenseNet

• In ResNet, we added the input and the output of the layer element-wisely
  • ResNet 에서는 skip connection 을 통해서 전달된 identity mapping 을 더했지만
• In the Dense blocks , every output of each layer is concatenated along the channel axis
  • Dense block 에서는 채널 축으로 concatenate하게 설계가 되있다
    • dense connection은 바로 직전 블록의 입력을 넘겨주는 것 뿐만 아니라 훨씬 이전의 layer에 대한 정보들도 넘겨주게 된다
    • 그래서 이전의 출력들도 모든 connection에 다 이어주는 형태로 dense 하게 설계가 되있다
    • 이를 통해서 사위 layer에서도, 하위 layer 의 특징을 재참조해서 재활용할 수 있는 기회를 제공한다
    • 이렇게 함으로써 더 복잡한 mapping의 학습이 용이하도록 도와주는 역할을 하게 된다
  • Alleviate the vanishing gradient problem
  • strengthen feature propagation
  • encourage the reuse of features
• concatenate 은 채널은 늘어나지만 신호는 보존한다는 장점이 있다
  • 채널이 늘어나서 메모리나 computational complexity는 늘어나는 대신에 feature의 정보를 그대로 보존하고 있어서 상위 layer에서 하위 layer의 참조할 필요성이 있을때는 잘 꺼내 사용할 수 있다
    

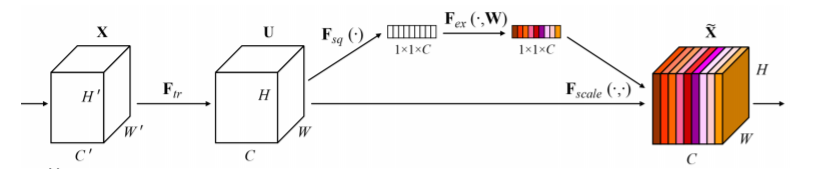
SENet

• depth를 높이거나 connection을 새로하는 방법이 아니라 현재 주어진 activation 간의 관계가 더 명확해질 수 있도록 채널 간의 관계를 모델링하고 중요도를 파악해서 중요한 특직을 attention할 수 있게끔 만들어주는 방법
• Attention across channels
• Recalibrates channel-wise responses by modeling interdependancies between channels
• squeeze and excitation operations
  • Squeeze : capturing distributions of channel-wise responses by global average pooling
    • global average pooling을 통해서 각 채널의 공간 정보를 없애고 각 채널의 분포를 구한다
  • Excitation : gating channels by channel-wise attention weights obtained by a FC layer
    • FC layer하나를 통해서 채널간의 연관성을 고려해서 채널을 gating 하기 위한 attention weights를 생성한다
  • 이렇게 나온 attention weights로 입력 attention하고 같이 활용해서 activation을 re-scaling 한다
  • 중요도가 떨어지는 거는 gating 되도록 즉 값을 낮추고 그리고 중요도가 높다고 생각하는 것은 더욱 강하게 값을 올린다
    

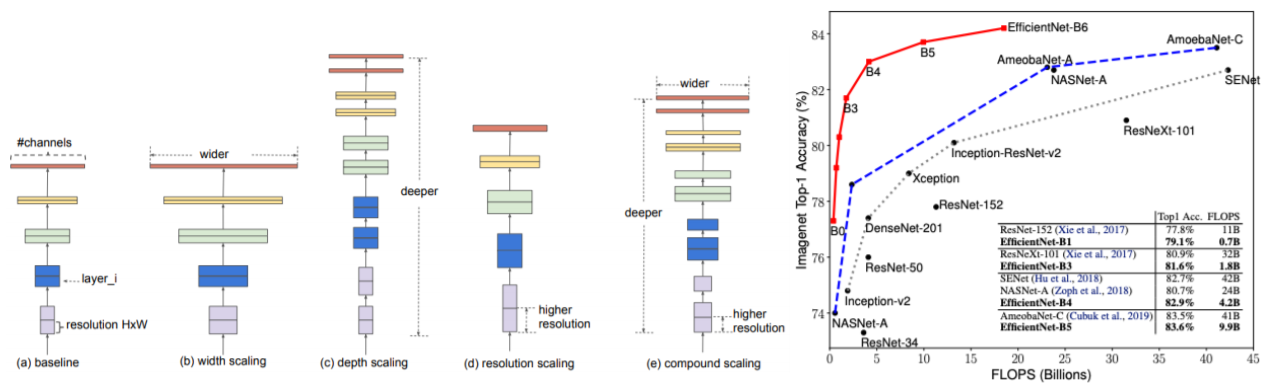
EfficientNet

• Building deep, wide, and high resolution networks in an efficient way
  • width scaling: 채널 축을 늘린다, 수평 확장
    • GoogLeNet의 inception model을 참조
    • DenseNet 참조
  • depth scaling: layer을 더 많이 쌓는다, 수직 확장
    • ResNet 을 참조
  • resolution scaling: input 이미지의 resolution을 애초에 큰걸 넣는 방식
    • input resolution을 큰걸 넣으면 성능이 향상이 된다
• 이렇게 3가지의 main factor들이 있는데 width, depth, resolution scaling 각각 어느정도 하면 성능의 증가 폭이 saturation이 된다
  • saturation 되는 증가폭이 서로 다르다
  • 그래서 이 3개를 적절하게 어떤 비율로 동시에 scaling을 해서 네트워크를 설계하면 더욱 효과적인 모델이 나온다
  • 그래서 compound scaling이라고 해서 위 3개의 factor를 적절한 비율로 조절해서 동시에 활용
    

Deformable convolution

• 2D spatial offset prediction for irregular convolution
• irregular 한 convolution operation 이 필요한 이유는
  • 자동차나 어떤 물건 같은 정해진 형태 (deformable한 파트가 없는) 반면
  • 사람 혹은 동물을 인식할 때는 굉장히 형태(팔, 다리, 몸 위치 등)가 바뀌기 때문에 이런 deformable을 고려한 convolution이 피요하다
• Irregular grid sampling with 2D spatial offsets
• Implemented by standard CNN and grid sampling with 2D offsets
  
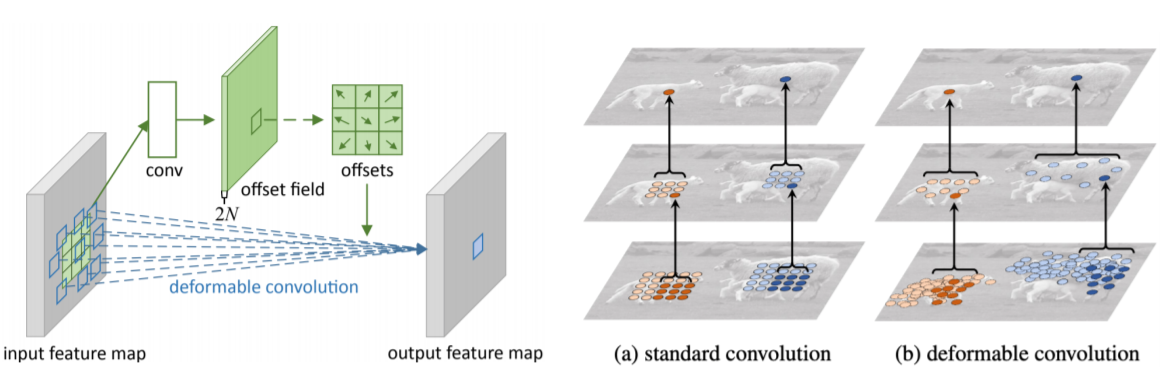
• 표준 convolution 외에 2D offset map을 추정하기 위한 branch가 따로 결합이 된다
  • convolution layer를 통해서 input이 들어왔을때 offset field를 생성하게 되고
  • offset field에 따라서 각각의 weight 들을 옆으로 벌려준다
  • 그러면 이 위치에 맞게끔, irregular한 sampling을 통해서 activation과 irregular한 filter를 내적해서 한가지 값을 도출한다

Summary of image classification

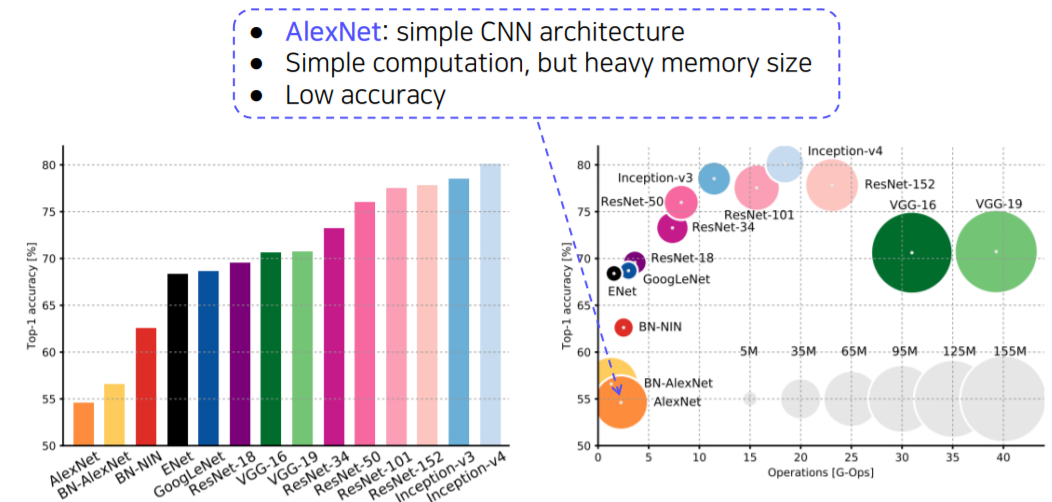
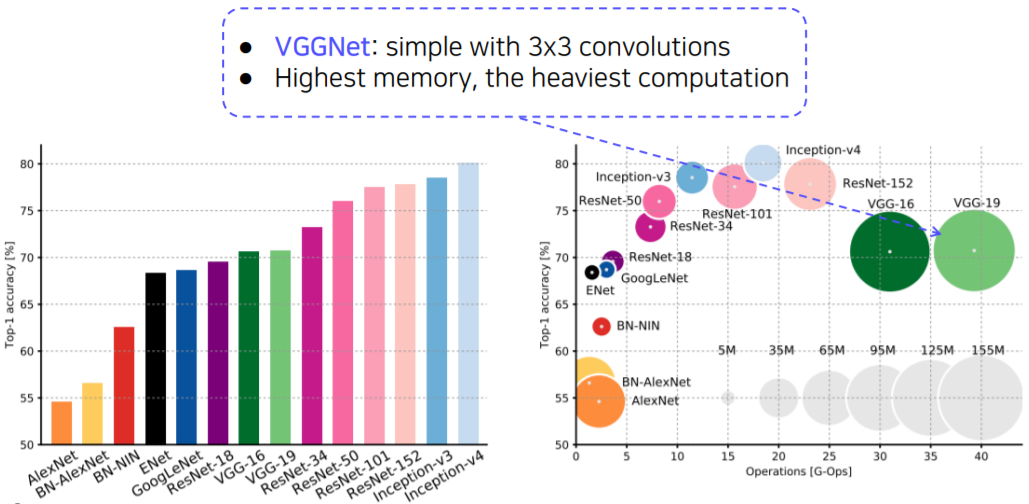
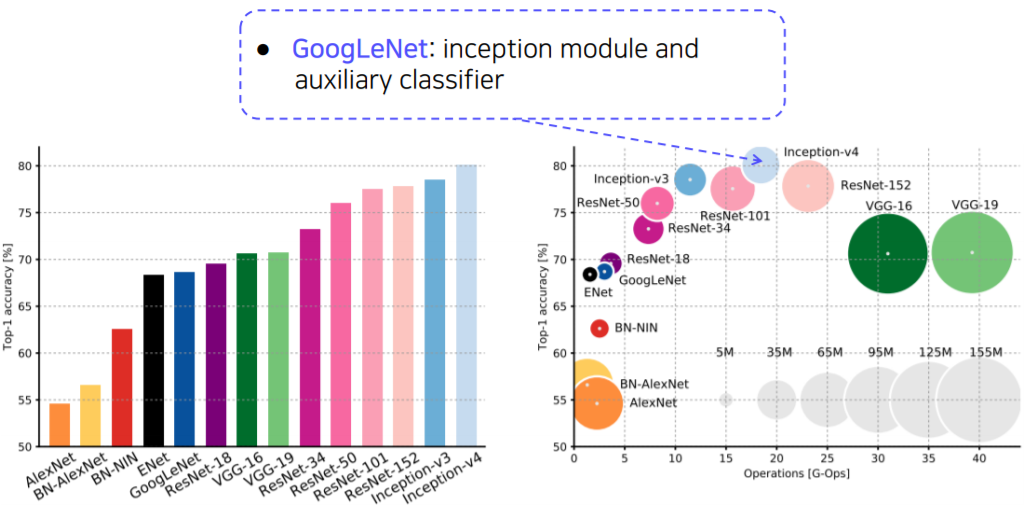
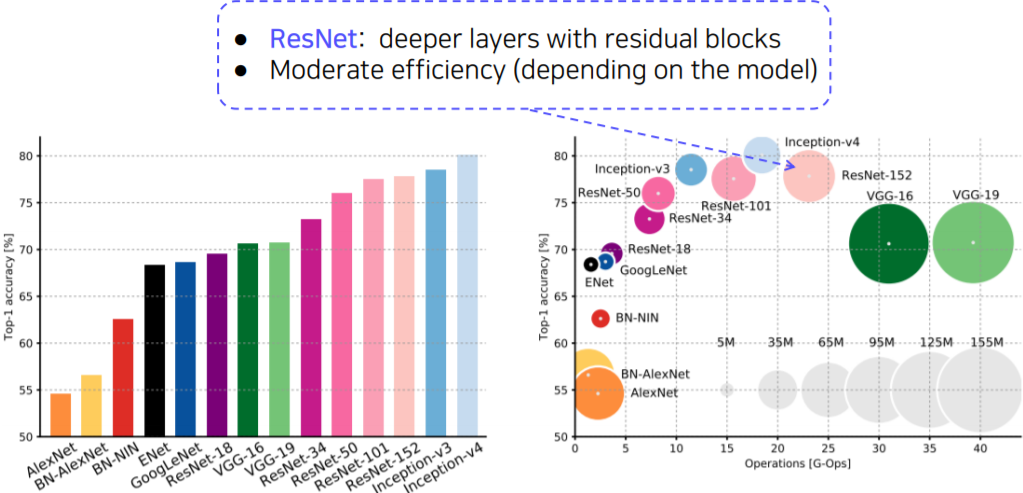
CNN backbones

• Simple but powerful backbone model
  • GoogLeNet is the most efficient CNN model out of {AlexNet, VGG, ResNet}
  • But, it is complicated to use
  • instead, VGGNet and ResNet are typically used as a backbone model for many tasks
  • Constructed with simple 3x3 conv layers
    

Reference

• CNN architectures for image classification 2
  • Szegedy et al., Going Deeper with Convolution, CVPR 2015
  • He et al., Deep Residual Learning for Image Recognition, CVPR 2015
  • Veit et al., Residual Networks Behave Like Ensembles of Relatively Shallow Networks, NIPS 2016
  • Huang et al., Densely Connected Convolutional Networks, CVPR 2017
  • Hu et al., Squeeze-and-Excitation Networks, CVPR 2018
  • Tan and Le, EfficientNet: Rethinking Model Scalinng for Convolutional Neural Networks, ICML 2019
  • Dai et al., Deformable Convolutional Networks, ICCV 2017
• Summary of image classification
  • Canziani et al., An Analysis of Deep Neural Network Models for Practical Applications, CVPR 2016