그래프의 정점을 어떻게 벡터로 표현할까?
- 그래프의 정점을 벡터로 표현하는 방법인 정점 임베딩(Node Embedding)에 대해서 배운다
- 기계학습의 다양한 툴은 벡터로 표현된 데이터를 입력으로 받는다
- 이러한 툴들을 이용해서 그래프를 분석할 수 있을까?
- 그래프를 벡터로 나타낼 수 있으면 가능하다
- 정점을 어떻게 벡터로 표현하는지, 정점 사이의 유사성을 어떻게 표현하는 지 집중하자
Further Readings
- node2vec: Scalable Feature Learning for Networks
- DeepWalk: Online Learning of Social Representations
정점 표현 학습
정점 표현 학습이란?
-
정점 표현 학습 이란 그래프의 정점들을 벡터의 형태로 표현 하는 것이다__
- 정점 표현 학습은 간단히 정점 임베딩(Node Embedding) 이라고도 부른다
- 정점 임베딩은 벡터 형태의 표현 그 자체를 의미 하기도 한다
- 정점이 표현되는 벡터 공간을 임베딩 공간 이라고 부르자
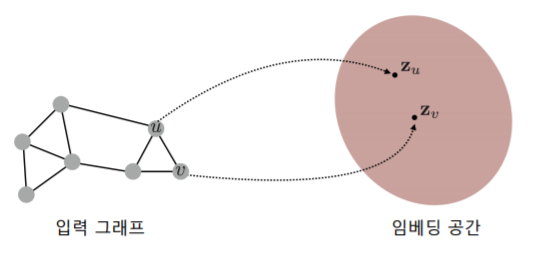
-
정점 표현 학습의 입력은 그래프다
- 주어진 그래프의 각 정점 에 대한 임베딩, 즉 벡터 표현 가 정점 임베딩의 출력 이다
- 출력 embedding의 차원을 로 표현한다
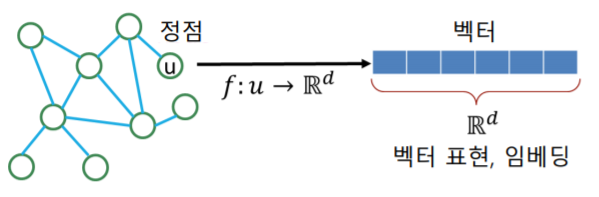
- 출력 embedding의 차원을 로 표현한다
- 주어진 그래프의 각 정점 에 대한 임베딩, 즉 벡터 표현 가 정점 임베딩의 출력 이다
정점 표현 학습의 이유
- 정점 임베딩의 결과로, 벡터 형태의 데이터를 위한 도구들을 그래프에도 적용할 수 있다
- 기계학습 도구들이 한가지 예시이다
- 대부분 분류기 (로지스틱 회귀분석, 다층 퍼셉트론 등) 그리고 군집 분석 알고리즘(K-Means, DBSCAN 등) 은 벡터 형태로 표현된 사례(Instance) 들을 입력으로 받는다
- 그래프의 정점들을 벡터 형태로 표현할 수 있다면, 위의 예시와 같은 대표적인 도구들 뿐 아니라, 최신의 기계 학습도구들을 정점 분류(Node Classification), 군집 분석(Community Detection) 등에 활용할 수 있다
- 지금까지 graph 노트들에서 살펴본 결과 이전 까지는 그래프 형태의 데이터를 처리하기 위하여 그래프 데이터에 특화된 별도에 알고리즘을 만들어야 한다는 수고스러움이 있었다
- 하지만 그래프의 정점들을 벡터형태로 표현할 수 있다면 그래프를 위한 별도의 알고리즘이 아닌 대표적인/최신의 기계학습 도구들을 그래프 데이터에도 활용할 수 있다는 장점이 있다
- 기계학습 도구들이 한가지 예시이다
정점 표현 학습의 목표
-
어떤 기준으로 정점을 벡터로 변환해야할까?
- 그래프에서의 정점간 유사도를 임베딩 공간에서도 “보존”하는 것 을 목표로 한다
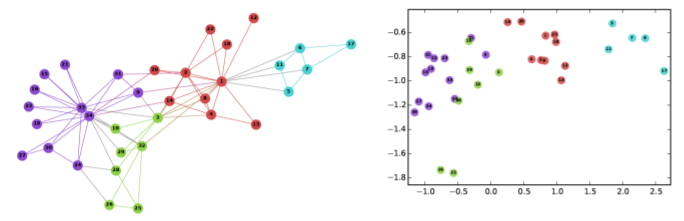
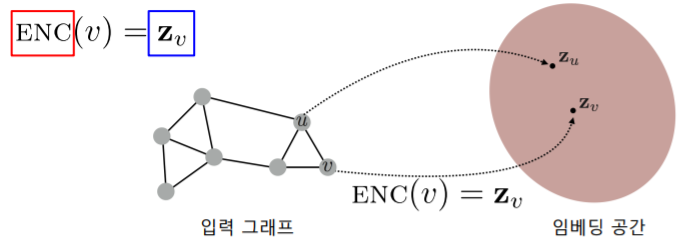
- 위 그림을 통해 살펴보면 입력 그래프가 있고 2차원의 embedding 공간이 있다
- 입력 그래프에 있는 각 정점들이 2차원 embedding 공간에 점, 즉 차원 벡터로 표현되게 된다
- 보라색 정점들을 보면 입력 그래프에서 서로 유사하다고 할 수 있다
- 즉, 서로 가깝게 위치해 있다
- 2차원 embedding 공간을 보더라도 보라색 공간들은 서로 유사한 벡터로 표현된것을 볼 수 있다
- 즉, 정점 표현학습의 목표는 입력 그래프에서 서로 유사한 정점들이 embedding 공간에서도 서로 유사하게 하는 것과 동시에 입력 그래프에서 유사도가 떨어지는 정점들은 embedding 공간에서도 유사도가 떨어지도록 하는 것이다
- 그래프에서의 정점간 유사도를 임베딩 공간에서도 “보존”하는 것 을 목표로 한다
-
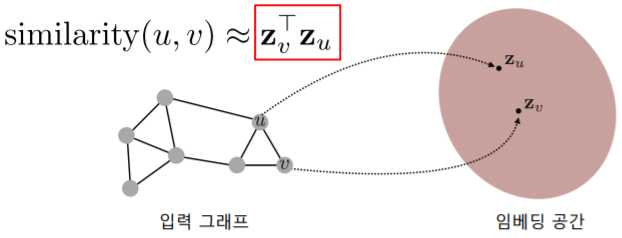
임베딩 공간에서의 유사도로는 내적(Inner Product) 를 사용한다
- 임베딩 공간에서의 와 의 유사도는 둘의 임베딩의 내적 이다
- 내적은 두 벡터가 클 수록, 그리고 같은 방향을 향할 수록 큰 값을 갖는다
-
그래프에서 두 정점의 유사도는 어떻게 정의할까?
- 이 질문에는 여러가지 답이 있을 수 있다
- 여기서는 대표적인 답 몇 가지를 설명한다
-
정리하면, 정점 임베딩은 다음 두 단계로 이루어진다
- 그래프에서의 정점 유사도를 정의 하는 단계
- 정의한 유사도를 보존하도록 정점 임베딩(벡터 표현)을 학습 하는 단계
인접성 기반 접근법
-
인접성(Adjacency) 기반 접근법 에서는 두 정점이 인접할 때 유사 하다고 간주한다
- 두 정점 와 가 인접 하다는 것은 둘을 직접 연결하는 간선 ()가 있음을 의미한다
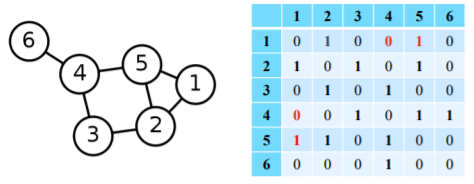
- 인접행렬(Adjacency Matrix) 의 행 열 원소 는 와 가 인접한 경우는 1 아닌 경우는 0이다
- 인접행렬의 원소 를 두 정점 와 의 유사도 로 가정한다
-
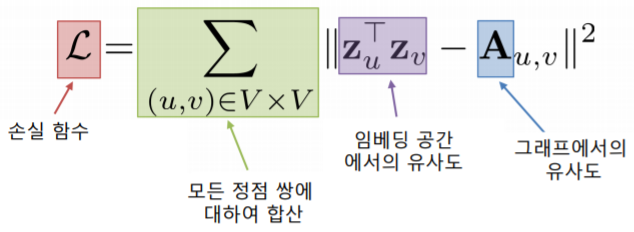
인접성 기반 접근법의 손실 함수(Loss Function) 는 아래와 같다
- 이 손실 함수가 최소가 되는 정점 임베딩들()을 학습하는 것 을 목표로 한다
- 즉, 이 정점 임베딩들이 인접성 기반 접근법의 출력(output) 이 되게 된다
- 손실 함수 최소화를 위해서는 (확률적) 경사하강법 등이 사용된다
- 이 손실 함수가 최소가 되는 정점 임베딩들()을 학습하는 것 을 목표로 한다
인접성 기반 접근법의 한계
- 인접성만으로 유사도를 판단하는 것은 한계가 있다
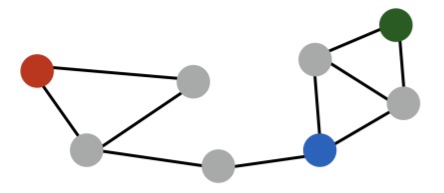
- 빨간색 정점과 파란색 정점 은 거리가 3인 반면 초록색 정점 과 파란색 정점__ 은 거리가 2이다
- 군집 관점에서는 빨간색 정점 과 파란색 정점 은 다른 군집에 속하는 반면 초록색 정점 과 파란색 정점 은 같은 군집에 속한다
- 이런 명백한 차이가 존재함에도 불구하고 인접성만을 고려하여 유사도를 판단할 경우, 빨간색, 파란색 정점들의 유사도와 초록색, 파란색 정점들의 유사도도 0으로 같다
- 즉, 인접성 만으로 유사도를 판단하는 것은 그래프 상에서의 거리를 무시한다는 점과 그래프에서의 군집 관계를 무시한다는 점 등 여러가지 한계를 갖는다
- 즉, 인접성 만으로 유사도를 판단하는 것은 그래프 상에서의 거리를 무시한다는 점과 그래프에서의 군집 관계를 무시한다는 점 등 여러가지 한계를 갖는다
거리/경로/중첩 기반 접근법
- 인접성 기반 접근법의 한계를 극복하고자 다양한 접근법들이 제안되었다
거리 기반 접근법
- 거리 기반 접근법 에서는 두 정점 사이의 거리가 충분히 가까운 경우 유사하다고 간주한다
- 예를 들어, “충분히”의 기준을 2로 가정하자
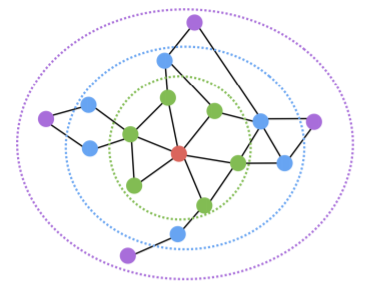
- 아래 빨간색 정점은 초록색 그리고 파란색 정점들과 유사하다
- 즉 유사도가 1이다
- 반면, 빨간색 정점은 보라색 정점과는 유사하지 않다
- 즉 유사도가 0이다
- 즉 유사도가 0이다
경로 기반 접근법
-
경로 기반 접근법 에서는 두 정점 사이의 경로가 많을 수록 유사하다고 간주한다
- 정점 와 의 사이의 경로(Path) 는 아래 조건을 만족하는 정점들의 순열(Sequence)이다
- 에서 시작해서 에서 끝나야 한다
- 순열에서 연속된 정점은 간선으로 연결되어 있어야 한다
- 경로가 아닌 순열의 예시:
- 1, 6, 8
- 1, 3, 4, 5, 6, 8
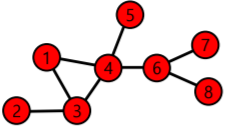
- 정점 와 의 사이의 경로(Path) 는 아래 조건을 만족하는 정점들의 순열(Sequence)이다
-
두 정점 와 의 사이의 경로 중 거리가 인 것들을 고려하게 된다
- 두 정점 와 의 사이의 경로 중 거리가 인 것은 와 같다
- 즉, 인접 행렬 의 제곱의 행 열 원소와 같다
- 따라서 경로 기반 접근법의 손실 함수는 다음과 같다
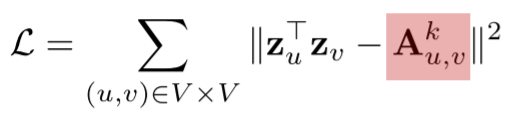
- 의 과정
- 인접행렬 를 번 만큼 내적 한 행렬의 행 열 원소의 값은 의 거리로 에서 까지 가는 경로의 수를 나타낸다
- : embedding 으로 부터 근사한 경로의 수와 실제 거리가 인 경로의 수를 비교하게 된다
- 이 차이가 작으면 작을수록 좋고 이 차이의 제곱을 하기때문에 이 차이가 크면 클수록 손실함수가 커지게 된다
- 는 길이 인 경로만을 고려하는 adjacency matrix라서, 해당 식대로 유사성을 구하면 보다 짧은 길이의 경로들에 대한 유사성이 고려되지 않아 문제가 생길 여지가 있다
- term을 term으로 바뀌는 것이 더욱 합리적이다
- 의 과정
중첩 기반 접근법
- 중첩 기반 접근법 에서는 두 정점이 많은 이웃을 공유 할 수록 유사하다고 간주한다
- 아래 그림에서 빨간색 정점은 파란색 정점과 두 명의 이웃을 공유하기 때문에 유사도는 2가 된다
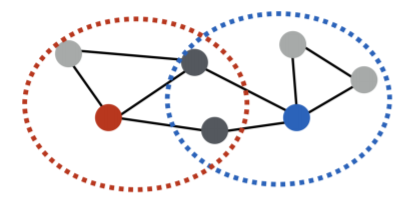
- 정점 의 이웃 집합을 그리고 정점 의 이웃 집합을 라고 하면 두 정점의 공통 이웃 수 는 다음과 같이 정의 된다
- 의 이웃 집합과 의 이웃 집합의 교집합의 크기
- 중접 기반 접근법의 손실 함수는 다음과 같다
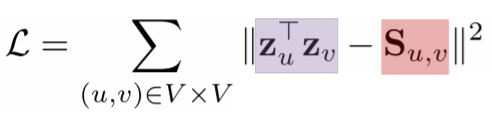
- 출력인 정점 embedding 벡터들은 그 내적값이 두 정점의 공통 이웃의 수를 근사해야한다
- 아래 그림에서 빨간색 정점은 파란색 정점과 두 명의 이웃을 공유하기 때문에 유사도는 2가 된다
- 공통 이웃 수를 대신 자카드 유사도 혹은 Adamic Adar 점수 를 사용할 수도 있다
- 자카드 유사도(Jaccard Similarity) 는 공통 이웃의 수 대신 비율을 계산하는 방식이다
- 분자 : 의 공통 이웃
- 분모 : 이웃들과 의 이웃들의 합집합의 크기
- 항상 분모가 분자보가 크기때문에 자카드 유사도의 값은 0~1 사이의 값을 가진다
- 이 자카드 유사도가 1을 갖는 경우는 와 가 완벽하게 동일한 경우이다
- 즉 두 정점의 이웃들의 집합이 완벽하게 동일할때 자카드 유사도가 1이 된다
- Adamic Adar 점수 는 공통 이웃 각각에 가중치를 부여하여 가중합을 계산하는 방식이다
- 와 의 공통이웃 에 대해서 이 의 연결성이 크면 클수록 가중치는 낮다
- 왜 연결성이 높은 공통이웃을 가질 때 가중치는 낮게 잡아야 하는것일까?
- 예시: 트위터 계정 와 가 있다고 가정
- 와 는 모두 아이유의 팬으로 아이유의 트위터 계정을 팔로우 한다
- 하지만 아이유 계정은 팔로워 수가 매우 많다
- 따라서 와 이외에도 수백만명의 팔로우들을 가지고 있다
- 이 경우 와 가 공통적으로 아이유를 팔로우 한다는 사실이 와 가 가까운 사이 일 것이라는 강한 시그널이 되진 않는다
- 왜냐하면 아이유 계정을 팔로우 하는 수백만명 중에 두 명일 뿐이기 때문이다
- 따라서 아이유 계정처럼 연결성이 매우 높은 계정을 공통 지인으로 갖고 있는것은 가중치가 크지 않다
- 예시: 트위터 계정 와 가 있다고 가정
- 따라서 연결성이 높은 공통 지인을 가질 경우 분모가 커지게 되고 가중치는 작아지게 된다
- 반대로 연결성이 낮은 공통 지인을 가질 경우 분모가 작게 되고 가중치는 커지게 된다
- 이런 방식으로 공통 이웃 각각에 대하여 가중치를 계산하여 이 가중치의 합으로 최종 adamic adar 점수를 계산하게 된다
- 자카드 유사도(Jaccard Similarity) 는 공통 이웃의 수 대신 비율을 계산하는 방식이다
임의보행 기반 접근법
- 임의보행 기반 접근법 에서는 한 정점에서 시작하여 임의보행을 할 때 다른 정점에 도달할 확률 을 유사도로 간주한다
- 임의보행 이란 현재 정점의 이웃 중 하나를 균일한 확률로 선택하는 이동하는 과정을 반복하는 것을 의미한다
- 임의보행을 사용할 경우 시작 정점 주변의 지역적 정보 와 그래프 전역 정보 를 모두 고려한다는 장점이 있다
- 시작 정점 주변을 많이 탐색하게 되므로 지역적 정보 를 사용한다는 것은 자명하다
- 기존의 거리/경로 기반 접근법에서는 그 거리를 로 제한했었다
- 하지만 임의보행 접근법에서는 거리를 제한하지 않는다
- 이러한 점에서 그래프 전역 정보 를 고려한다고 할 수 있다
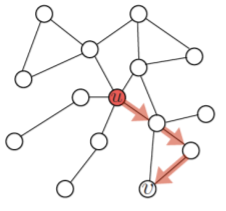
- 임의보행 기반 접근법 은 세 단계를 거친다:
- 각 정점에서 시작하여 임의보행을 반복 수행한다
- 각 정점에서 시작한 임의보행 중 도달한 정점들의 리스트를 구성한다
- 이 때, 정점 에서 시작한 임의보행 중 도달한 정점들의 리스트를 라고 하자
- 한 정점을 여러 번 도달한 경우, 해당 정점은 에 여러 번 포함될 수 있다
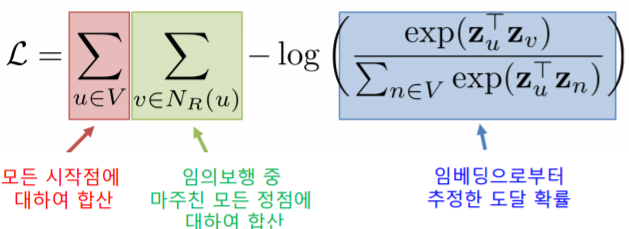
- 다음 손실함수를 최소화하는 임베딩을 학습한다
- 각 시작전 에서 임의보행을 통해 도달한 를 고려하게 된다
- 즉 에서 임의보행을 통해 실제로 에 도달한 것을 의미한다
- : 에서 시작한 임의보행이 에 도달할 확률을 임베딩으로부터 추정한 결과를 의미한다
- 확률값이 크면 클수록 추정을 잘 한것이다
- 그렇기 때문에 -log 값은 작으면 작을수록 좋다는 의미도 된다
- 따라서 최소화하는 손실함수는 -log 확률들의 합으로 정의된다
- 각 시작전 에서 임의보행을 통해 도달한 를 고려하게 된다
- 어떻게 임베딩으로부터 도달 확률을 추정할까?
- 정점 에서 시작한 임의보행이 정점 에 도달할 확률 을 다음과 같이 추정한다
- 사이의 embedding의 내적값의 exp 값의 정규화(모든 정점에 대해서 내적값의 exp을 계산)
- 즉 유사도 가 높을 수록 도달 확률이 높다
- 정점 에서 시작한 임의보행이 정점 에 도달할 확률 을 다음과 같이 추정한다
- 추정한 도달 확률 을 사용하여 손실함수 를 완성하고 이를 최소화하는 임베딩을 학습한다
DeepWalk와 Node2Vec
- 임의보행의 방법에 따라 DeepWalk 와 Node2Vec 이 구분된다
- DeepWalk 는 앞서 설명한 기본적인 임의보행 을 사용한다
- 즉, 현재 정점의 이웃 중 하나를 균일한 확률 로 선택하여 이동하는 과정을 반복한다
- Node2Vec 은 2차 치우친 임의보행(Second-order Biased Random Walk) 을 사용한다
- 현재 정점 (예시에서 )과 직전에 머물렀던 정점 (예시에서 )을 모두 고려하여 다음 정점을 선택한다
- 직전 정점의 거리를 기준으로 경우를 구분하여 차등적인 확률을 부여한다
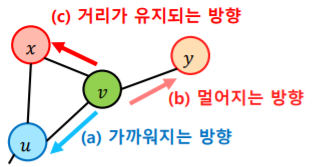
- 에서부터 임의보행을 시작하여 에 도달했다고 가정해보자
- 그러면 의 이웃중 하나를 선택하여 임의보행을 계속해야 한다
- 하지만 로 돌아갈수도 있고 혹은 로 갈수 있다
- 로 돌아간다는 것은 이전에 있던 정점과 더 가까워지는 방향이고
- 로 간다는 것은 이전에 있던 정점과 거리가 유지되는 방향이다
- 즉 사이의 거리도 1이고 사이의 거리도 1이다
- 한편 로 간다는 것은 이전에 있던 정점 로 부터 더욱 멀어지는 것을 의미한다
- 이런 기준으로 가까워지는 방향, 멀어지는 방향, 거리가 유지되는 방향으로 구분하여서 3경우에 대해 서로 차등적인 확률을 부여하여 임의 보행을 한다
- 차등적 확률은 사용자가 결정한다
- DeepWalk 는 앞서 설명한 기본적인 임의보행 을 사용한다
- Node2Vec에서는 부여하는 확률에 따라서 다른 종류의 임베딩을 얻는다
- 아래 그림은 Node2Vec 으로 임베딩을 수행한 뒤, K-means 군집 분석을 수행한 결과이다
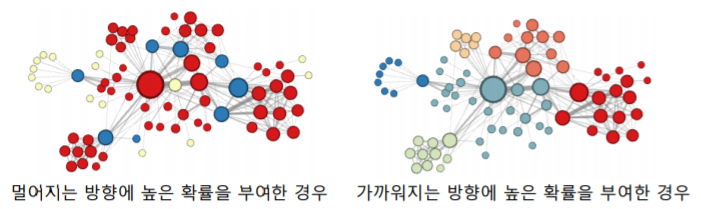
- 멀어지는 방향에 높은 확률을 부여하여 치우친 임의보행을 한 경우, 정점의 역할(다리 역할, 변두리 정점 등)이 같은 경우 임베딩이 유사 하다
- 파란색 정점들을 살펴보자
- 파란색 정점들은 서로 인접하진 않지만 서로 다른 군집들을 연결해주는 다리 역할을 하는 정점이다
- 노란색 정점들은 연결성이 높지 않은 그래프의 주변부의 위치하는 정점들이다
- 반면 빨간색 정점들은 군집에 속해 있는 정점들이다
- 즉, 이렇게 멀어지는 방향에 높은 확률을 부여한 경우 서로 비슷한 역할을 하는 정점들이 embedding 공간에서 유사한 벡터를 갖게 된다
- 파란색 정점들을 살펴보자
- 가까워지는 방향에 높은 확률을 부여한 경우, 같은 군집(Community)에 속한 경우 임베딩이 유사 하다
- 같은 색깔은 갖는 정점들은 같은 군집에 속해있다
- 즉, 가까워지는 방향에 높은 확률을 부여한 경우 같은 군집에 속하는 정점들이 embedding 공간에서 비슷한 벡터값을 갖게 된다
- 같은 색깔은 갖는 정점들은 같은 군집에 속해있다
- 아래 그림은 Node2Vec 으로 임베딩을 수행한 뒤, K-means 군집 분석을 수행한 결과이다
손실 함수 근사
- 임의보행 기법의 손실함수는 계산에 정점의 수의 제곱에 비례하는 시간이 소요된다
- 중첩된 합 때문이다
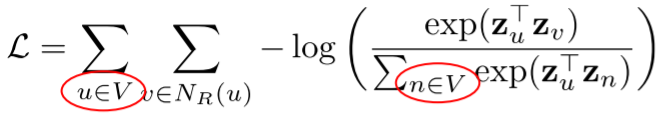
- 무려 3개의 이 존재하고 두개의 은 모든 정점의 대해서 합계를 낸다
- 따라서 임의 보행 기법의 손실함수를 계산하기 위해서는 정점의 수의 제곱의 비례하는 시간이 든다
- 정점이 많은 경우, 제곱은 매우 큰 숫자이다
- 예시로 1억의 제곱은 1경 = 10,000조 이다
- 중첩된 합 때문이다
- 이런 제곱합을 피하기 위해서 많은 경우 근사식을 사용한다
- 근사식의 핵심 아이디어는 :
- 모든 정점에 대해서 정규화 하는 대신 몇 개의 정점을 뽑아서 비교 하는 형태이다
- 이 때 뽑힌 정점들을 네거티브 샘플 이라고 부른다
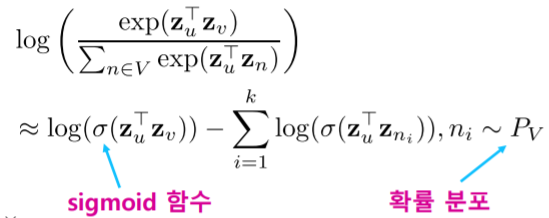
- 위 수식에서 분모 부분을 계산하는 것이 문제가 된다
- 모든 정점에 대해서 합산을 하기 때문이다
- 따라서 모든 정점에 대해서 합산을 하는 대신 개의 정점을 임의로 선발하여 그 정점에 대해서만 분모를 계산한다
- 함수의 형태도 함수를 사용하여 근사할 수 있다
- 즉 개의 샘플을 사용하여 모든 정점에 대해서 합산해야하는 부분을 근사하는 것이다
- 연결성에 비례하는 확률 로 네거티브 샘플 을 뽑으며, 네거티브 샘플 이 많을 수록 학습이 더욱 안정적이다
- 근사식의 핵심 아이디어는 :
변환식 정점 표현 학습의 한계
변환식 정점 표현 학습과 귀납식 정점 표현 학습
- 지금까지 소개한 정점 임베딩 방법들을 변환식(Transductive) 방법 이다
- 변환식(Transductive) 방법은 학습의 결과로 정점의 임베딩 자체 를 얻는다는 특성이 있다
- 정점을 임베딩으로 변화시키는 함수 , 즉 인코더 를 얻는 귀납식(Inductive) 방법과 대조된다
변환식 정점 표현 학습의 한계
-
변환식 임베딩 방법은 여러 한계를 갖는다
- 학습이 진행된 이후에 추가된 정점에 대해서는 임베딩을 얻을 수 없다
- 즉, 입력 그래프의 변화가 있는 경우 embedding을 처음부터 다시 수행해야 한다
- 모든 정점에 대한 임베딩을 미리 계산하여 저장해두어야 한다
- 예를들어 정점이 100만개면 100만개를 전부 벡터로 바꾸어서 저장해야 한다
- 정점이 속성(Attribute) 정보를 가진 경우에 이를 활용할 수 없다
- 즉 정점이 성별, 나이, 지역 등의 정보를 가지고 있더라도 그것을 embedding에 놀아낼 수 있는 방법이 변환식 방법에는 없다
- 성별, 나이, 지역 등의 정보를 가지고 있더라도, 변환식 방법에서 사용한 loss function에는 attribute에 대한 term(특정 attribute의 정보를 담고 있는 행렬)이 존재하지 않기 때문에 변환된 임베딩은 attribute 와 무관하다
- 학습이 진행된 이후에 추가된 정점에 대해서는 임베딩을 얻을 수 없다
-
다음에는 이런 단점을 극복한 귀납식 임베딩 방법을 소개한다
- 기존 변환식 방법은 의 ()를 학습하는 것이였다면, 귀납식 방법은 임베딩 변환 함수 자체를 학습하는 것이다
- 대표적인 귀납식 임베딩 방법이 바로 그래프 신경망(Graph Neural Network) 이다
-
출력으로 인코더를 얻는 귀납식 임베딩 방법 은 여러 장점을 갖는다
- 학습이 진행된 이후에 추가된 정점에 대해서도 임베딩을 얻을 수 있다
- 모든 정점에 대한 임베딩을 미리 계산하여 저장해둘 필요가 없다
- 그때 그때 필요한 정점에 대해서 함수를 적용해서 벡터를 얻어낼 수 있다
- 정점이 속성(Attribute) 정보를 가진 경우에 이를 활용할 수 있다
- 인코더 함수를 디자인 할 때 이 함수가 입력으로 속성 정보까지 활용할 수 있도록 함수의 구조를 설계한다

- 다음에 소개하는 그래프 신경망(Graph Neural Network) 은 대표적인 귀납식 임베딩 방법 이다
