그래프의 탐색 혹은 그래프의 순회라고 불리우는 개념은 그래프의 모든 정점을 반드시 한 번은 방문하는 것을 말합니다. 그래프의 탐색 방법에는 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 두 종류가 있는 그 중에서 깊이 우선 탐색 부터 알아보겠습니다.
깊이 우선 탐색 Depth First Search
깊이 우선 탐색(DFS, Depth First Search)은 한 정점에서 시작하여 한 방향으로 진행해 갈 수 있는 정점까지 최대한으로 탐색합니다. 그러다가 더이상 진행할 수 없다면 가장 최근에 만난 갈림길이 있는 정점으로 돌아가서 다른 방향의 간선으로 진행할 수 있는지 탐색하는 방식입니다.
깊이 우선 탐색에서는 탐색한 경로의 정보를 담기 위해서 스택을 이용하고, 정점에 대해 방문한 정보를 기록하기 위해서배열을 이용합니다.
말로했을 때 이해가 어려운 개념이기에 다시 한 번 그림으로 보여드리겠습니다. 아래와 같은 5개의 정점을 가진 그래프가 있고, 정점의 갯수 크기와 같은 배열과 빈 스택이 있습니다. 이때 배열은 초기화를 F(false)로 하는데 이는 방문했을 경우 T(True)로 변경하기 위함입니다.
A에서 탐색을 출발한다고 가정해보겠습니다.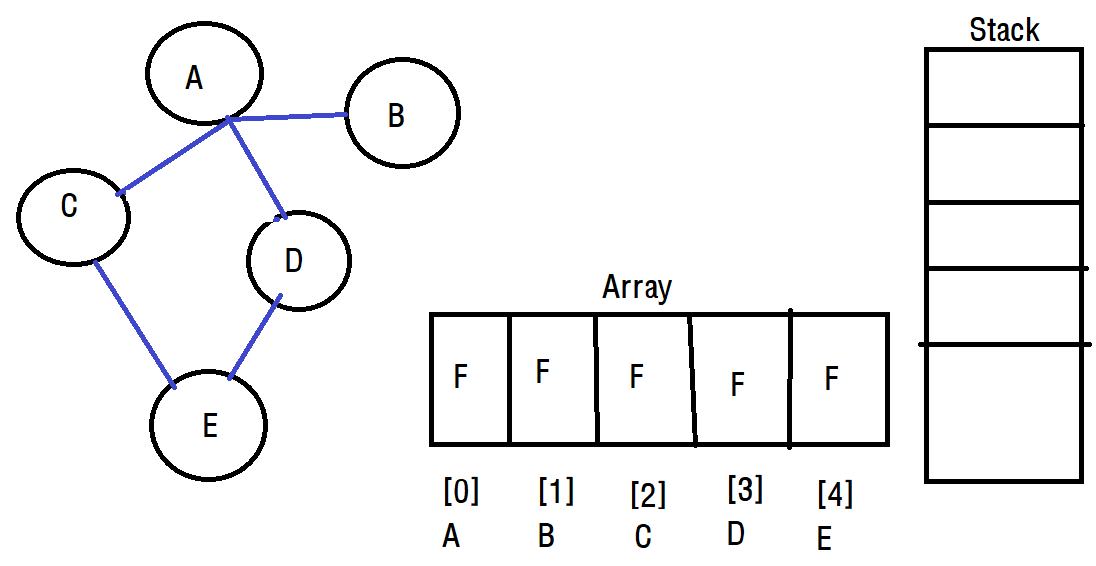
A를 방문했으니 배열의 A 정점 방문 정보를 T로 변경합니다. 다음 이동 노드는 오름 차순에 따라서 B로 이동하겠습니다.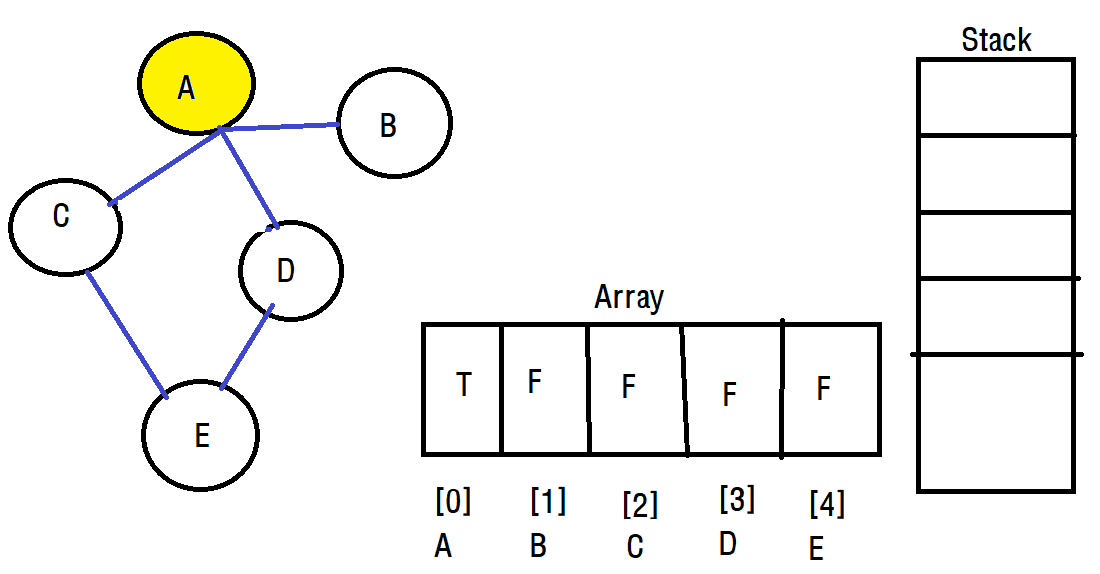
A에서 아직 방문하지 않은 정점인 B, C, D가 존재하는데 오름차순을 따라서 B로 이동하겠습니다. 이때 B로 이동하면서 스택에 A를 push합니다. 이때 스택에 push하는 시점은 정점을 떠나는 순간입니다.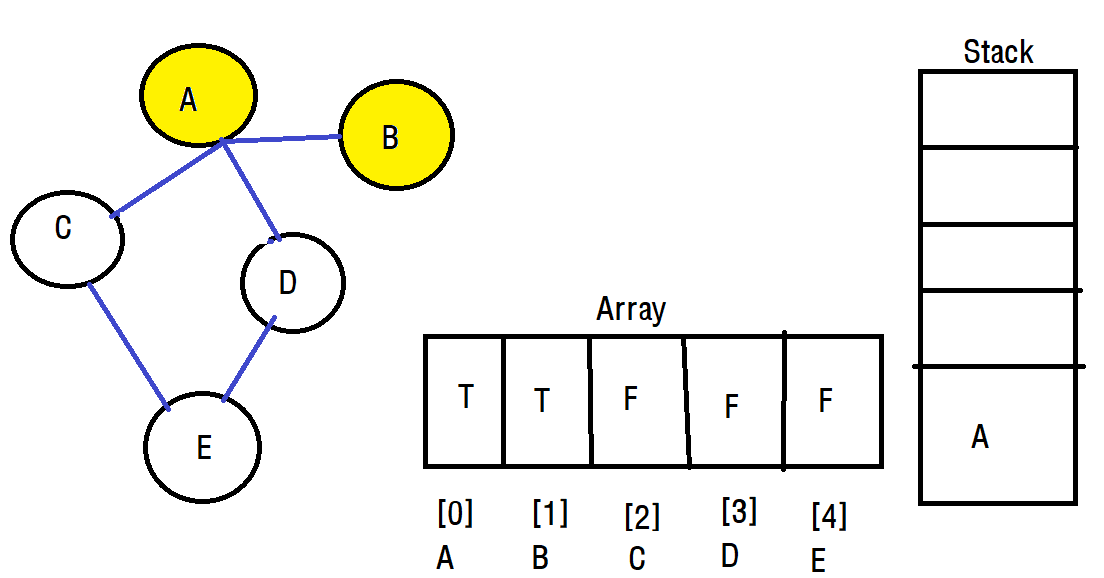
그리고 B에 방문하면 B도 스택에 푸시합니다. 여기서 문제가 발생합니다. 아직 방문하지 않은 노드가 있지만 B와는 연결이 되어있지 않습니다. 그래서 우리는 A 정점으로 돌아가야하는데 이 작업을 스택을 이용하게됩니다.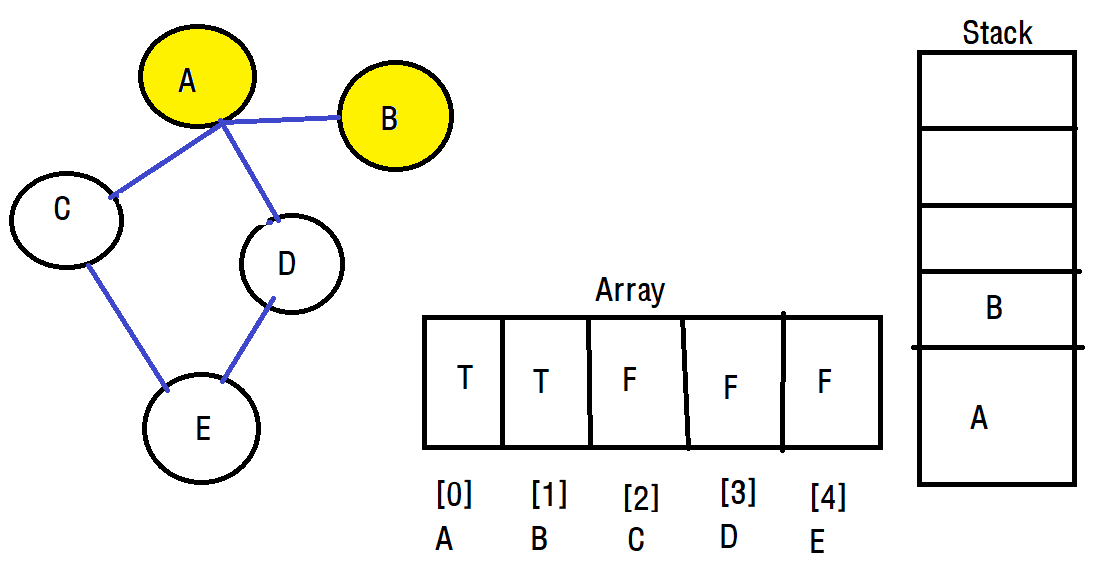
B를 스택에서 pop하게 되면 다시 A로 돌아와서 방문안한 정점이 있는지 다시 확인할 수 있습니다.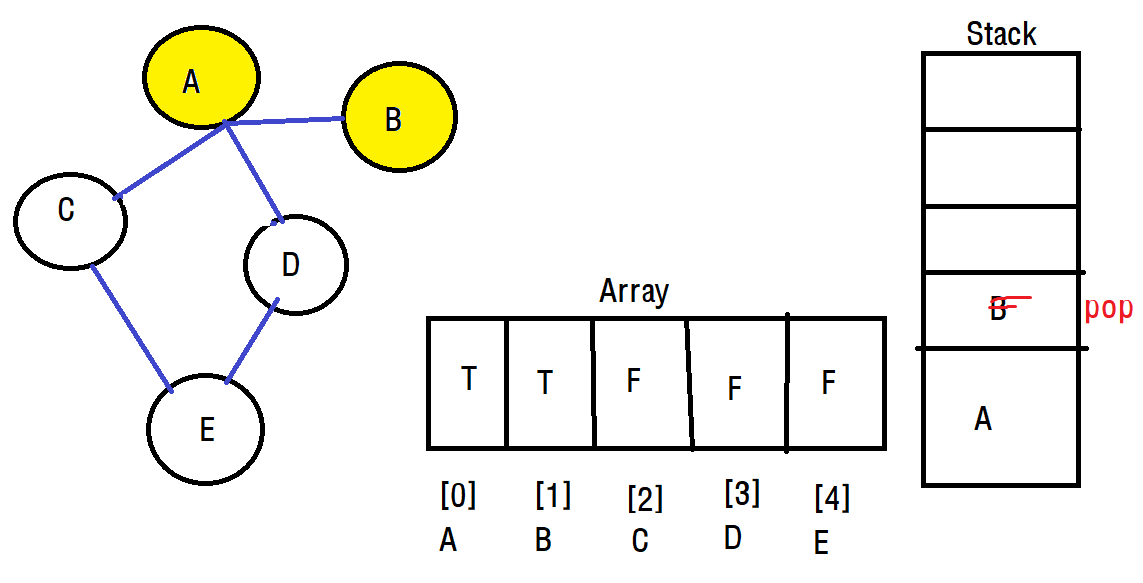
다시 A로 돌아왔으니 다시 A 정점에서 방문하지 않는 정점과 이어진 간선이 있는지 확인합니다. C, D가 존재하는데 C 부터 방문하겠습니다.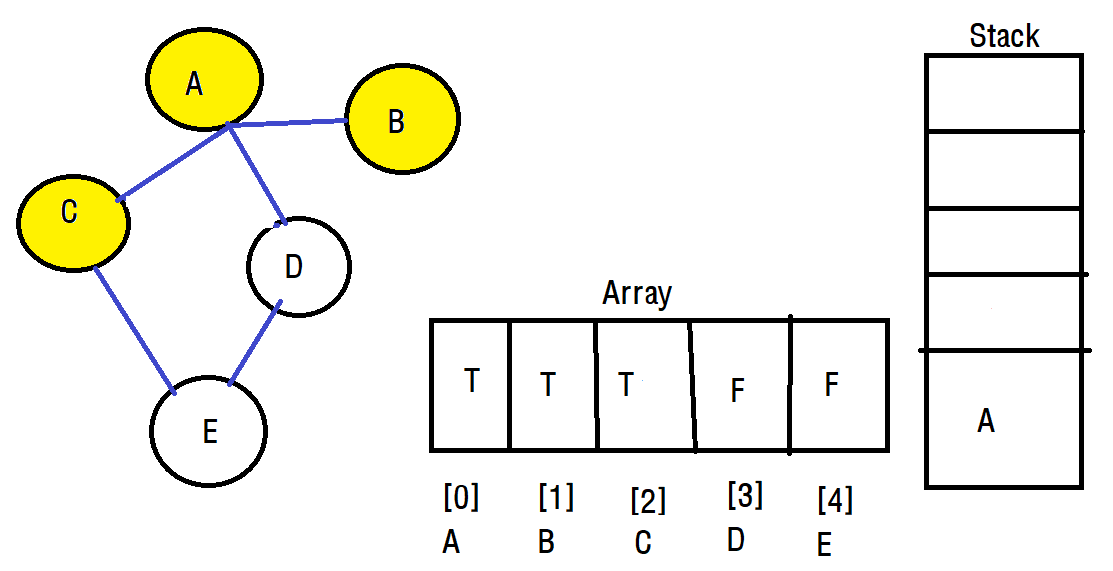
다음으로 C와 연결된 E로 이동하고, 마찬가지로 C를 스택에 push합니다.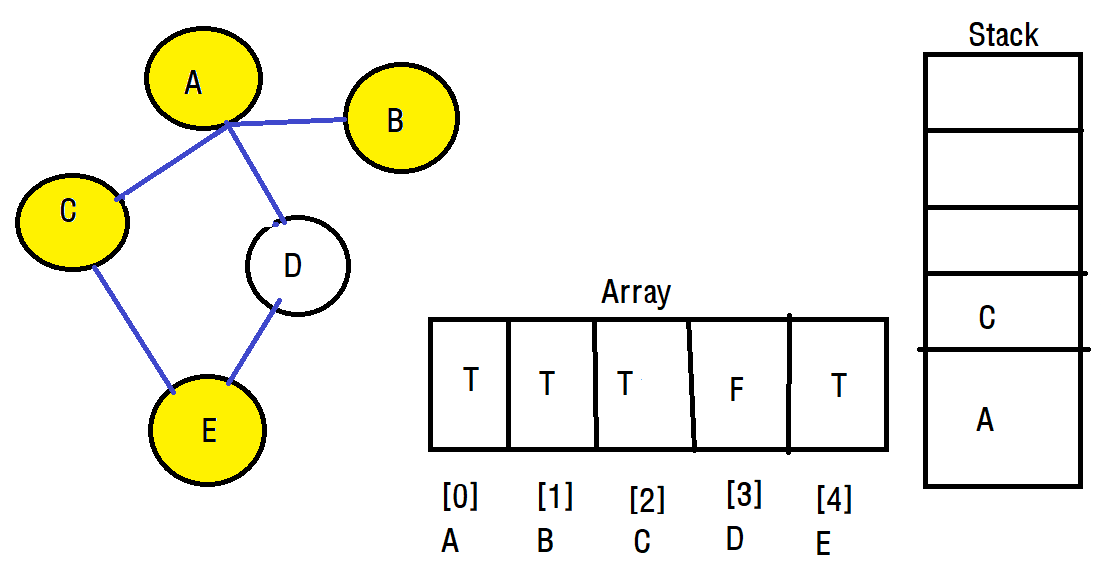
마지막으로 D에 방문하면 모든 정점에 방문을 하게됩니다. 그러나 사람인 우리는 다 돌았음을 알 수 있지만 컴퓨터는 그렇지 않기에 한가지 과정을 더 넣습니다.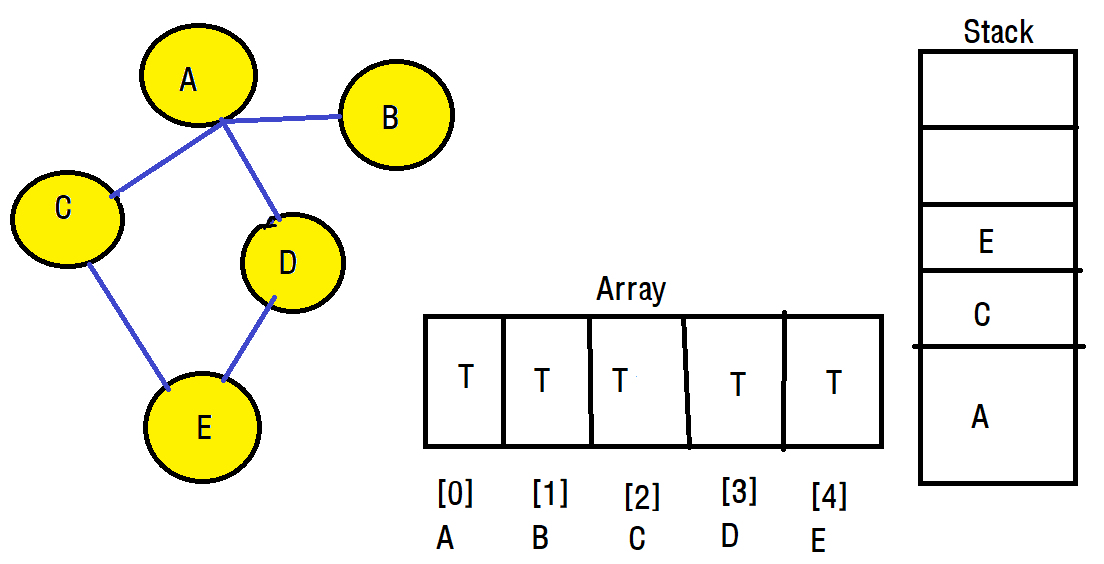
스택에 남아있는 방문 정보들을 POP하면서 마지막으로 방문하지 않은 정점이 존재하는지 확인합니다. 이렇게 스택이 모두 POP되서 비어있게 된다면 그래프의 깊이 우선 탐색이 종료됩니다.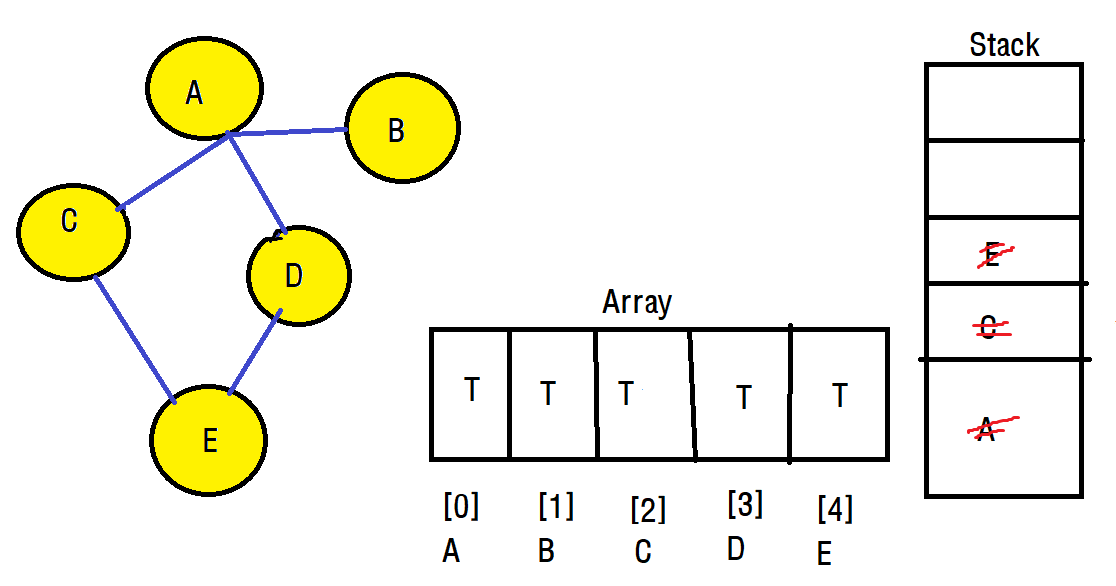
이 과정들에 따라서 깊이 우선 탐색을 구현해보겠습니다. 특히 스택을 이용해서 이전 정점으로 돌아가 다른 정점이 있는지 확인하는 작업 부분이 중요함을 염두에 두고말이죠.
DFS 구현
연결 리스트 기반 그래프를 기준으로 DFS를 구현합니다.
void DepthFirstSearch(graphType* g, int v) {
graphNode* currentNode; //현재 위치한 정점
top = NULL; //스택의 top 지정
push(v); //시작하는 정점이 v이므로 스택에 v부터 push
g->visitedNode[v] = TRUE; //정점 v를 떠났으므로 v의 방문정보를 TRUE로 설정
while (!isEmpty()) { //스택이 공백이 아닌동안에 DFS반복하기
v = pop(); //스택에서 pop된 정점을 v에 저장
//현재 노드를 정점v의 인접 리스트의 첫 번째 노드로 설정
//즉, v에서 가장 가까운 노드로 이동
currentNode = g->adjacentListHeadPointer[v];
//인접 정점이 존재하는 동안 반복
while (currentNode) {
//현재 정점이 방문했던 정점(TRUE, 1)이 아닌 경우
if (!g->visitedNode[currentNode->vertex]) {
if (isEmpty()) { //이동하기전 정점 v로 돌아오기 위해서 v를 push
push(v);
}
//현재 위치한 정점을 스택에 push
push(currentNode->vertex);
//현재 정점을 방문했으므로 TRUE로 설정
g->visitedNode[currentNode->vertex] = TRUE;
//다음 정점으로 이동하기 위해서 v를 현재 정점으로 설정
v = currentNode->vertex;
//바뀐 v에 대한 인접 리스트의 첫 번째 배열 변경
currentNode = g->adjacentListHeadPointer[v];
}
//현재 정점이 방문했던 정점인 경우
else {
//현재 정점과 연결된 다른 정점으로 이동
currentNode = currentNode->link;
}
}
} //스택이 공백이 되면 DFS 종료
}인접 리스트 그래프가 포함된 전체 코드는 GitHub에서 확인하실 수 있습니다.
