지난번엔 순차 자료구조인 2차원 배열을 이용한 인접 행렬 기반 그래프를 구현했습니다. 이번에는 연결 자료구조를 이용해서 그래프를 구현해보도록 하겠습니다.

인접 리스트 Adjacent List

인접 리스트 방식은 한 정점에 대해서 인접한 리스트를 연결 리스트로 연결한 것입니다. 다음과 같은 그래프를 인접 리스트로 표현해보면 다음과 같습니다.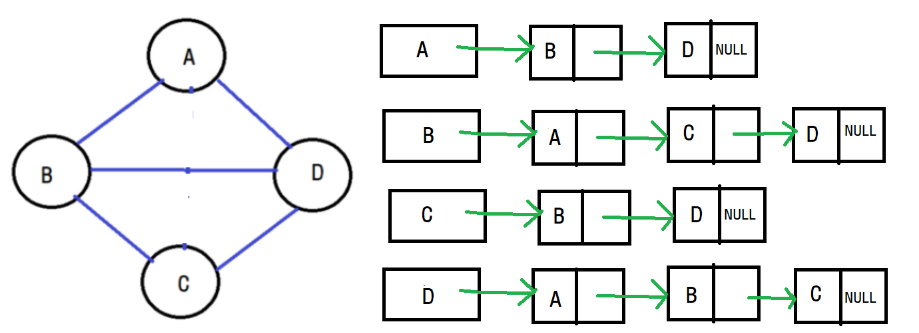그림을 보고나면 대충 감이 잡히실겁니다. 각 정점에 대해서 노드는 간선의 갯수만큼 연결되어있습니다. 맨 처음의 A, B, C, D 노드를 헤드 포인터라고 하며, 이 헤드 포인터는 그래프의 정점의 갯수만큼을 필요로합니다.

즉, 무방향 그래프의 노드의 수 만큼의 연결 리스트가 만들어지고 각 연결 리스트는 정점이 가진 간선의 갯수(차수, degree)만큼의 길이를 가지게 됩니다.

만약 방향 그래프라면 뻗어나간 간선의 수 만큼 연결 리스트 길이가 결정됩니다.

인접 리스트 그래프 구현

구조 정의

우선 기본 구조입니다. 연결 리스트 답게 노드 부터 정의하는데요, 마찬가지로 여태까지 이용한 노드의 구조인 데이터 필드-링크 필드 쌍을 이루고 있습니다. 하지만 같은 노드여도 그래프에서 데이터는 정점에 저장되기 때문에 정점(vertex)이라는 용어를 사용했습니다.

#define MAX_VERTEX 10

typedef struct graphNode {
	int vertex;	//정점(=데이터 필드)
	struct graphNode* link;	//링크 필드
}graphNode;

typedef struct graphType {
	int n;	//그래프의 정점 갯수 n
    //헤드 포인터들을 저장할 배열, 헤드 포인터 수 = 정점 수
	graphNode* adjacentListHeadPointer[MAX_VERTEX];
}graphType;

정점 삽입

인접 행렬과 비슷합니다. 정점을 삽입할 때 최대 정점수 보다 많으면 삽입을 취소하고 아니라면 정점수를 +1합니다.

void insertVertex(graphType* g, int v) {
	if (g->n + 1 > MAX_VERTEX) {
		return;
	}

	g->n++;
}

간선 삽입

간선의 주의점은 연결 리스트 이기 때문에 간선을 삽입한 다음에 삽입한 헤드 포인터 연결 리스트에 추가 시켜주는 작업이 필요합니다.

void insertEdge(graphType* g, int tail, int head) {
	graphNode* node;

	//간선을 이을 수 없는 상태라면(출발점이나 도착점이 현재 정점 n번 보다 크거나 같다면) 취소
	if ((tail >= g->n) || (head >= g->n)) {
		return;
	}

	
	node = (graphNode*)malloc(sizeof(graphNode));
	node->vertex = head;
    //간선을 삽입하고 노드를 해당 헤드 포인터 리스트에 연결시킵니다.
	node->link = g->adjacentListHeadPointer[tail];

	g->adjacentListHeadPointer[tail] = node;
}

---

인접 리스트 그래프의 전체 코드는 GitHub에서 확인하실 수 있습니다.