
🚀 짱 중요한 예제! 🚀
예제 9-1
직선 선로에서 열차가 80m/s의 속도를 유지하는지 시험해보자. 위치와 속도 정보는 0.1초 간격으로 측정해서 저장하도록 되어 있다.
시험 결과를 봤더니 속도 데이터가 모두 0이다. 위치 정보는 이상이 없다. 어떻게 하면 될까?
지금까지는 주로 측정 잡음을 효과적으로 제거하는 방법을 봤다.
잡음 제거는 칼만 필터보다 훨씬 간단한 구조를 가진 저주파 통과 필터로도 충분히 할 수 있다.
이번엔 위치 정보만 가지고 측정하지 않은 속도를 알아내야 한다.
이런 문제는 "측정" 신호의 잡음만 제거할 수 있는 저주파 통과 필터를 사용하지 못한다.
속도는 이동 거리를 시간으로 나눈 값이니, 짧은 시간 동안의 이동 거리를 그 시간으로 나누면 그 구간의 속도를 구할 수 있다.
하지만 실제로 적용해보면 오차가 크다.
잡음 때문에 측정 거리는 들쭉날쭉한데 분모의 시간은 아주 작아서, 나누면 값이 크게 튀기 때문!
➡ 칼만 필터❗
1. 시스템 모델
칼만 필터를 설계하기 위해 먼저 시스템 모델을 찾자!

설계한 시스템 모델이 예제의 내용을 제대로 반영하고 있는지 확인!


시스템 모델은 속도와 거리 사이의 물리적 관계, 속도에 영향을 주는 요인 등을 수학식으로 표현한 것!
A와 H는 임의로 선정한 것이 아니라, 시스템의 물리적인 관계를 모델링한 것
마지막으로 잡음의 공분산 행렬(Q,R)만 결정하면 시스템 모델의 유도가 끝난다.
- 측정 잡음(v_k)의 오차 특성은 센서 제작사에서 제공하는 경우가 많다.
- 시스템 잡음(w_k)의 모델링은 더 어려운데, 시스템에 대한 지식과 경험에 의존할 수 밖에 없다.
공분산 행렬(Q,R)을 논리적으로 구하기 어렵다면 두 행렬을 칼만 필터의 설계 인자로 보고 시행착오를 거쳐 선정하는 것도 하나의 방법!
이번 예제에선 아래의 특성을 갖는다고 가정
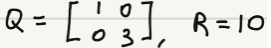
2. 칼만 필터 함수
DvKalman(z)
- 매개변수: z (위치 측정값)
- 반환값: 위치 추정값, 속도 추정값
시스템 모델만 있으면 칼만 필터 알고리즘 구현은 아무것도 아님!
📌 항상 문제는시스템 모델!!
DvKalman.m
function [pos, vel] = DvKalman(z)
%
%
persistent A H Q R
persistent x P
persistent firstRun
if isempty(firstRun)
firstRun = 1;
dt = 0.1;
A = [1 dt;
0 1 ];
H = [1 0];
Q = [1 0;
0 3];
R = 10;
x = [0 20]';
P = 5*eye(2); % eye(): identity matrix
end
xp = A*x;
Pp = A*P*A' + Q;
K = Pp*H' * inv(H*Pp*H' + R);
x = xp + K*(z - H*xp);
P = Pp - K*H*Pp
pos = x(1);
vel = x(2);
endGetPos.m (실전에서는 이런 함수를 쓰지 않고, 센서로 측정한 위치를 받아옴)
function z = GetPos()
%
%
persistent Velp Posp
if isempty(Posp)
Posp = 0;
Velp = 80;
end
dt = 0.1;
w = 0 + 10*randn;
v = 0 + 10*randn;
z = Posp + Velp*dt + v;
Posp = z - v; % true position
Velp = 80 + w; % true speed
endTestDvKalman.m
clear all
dt = 0.1;
t = 0:dt:10;
Nsamples = length(t);
Xsaved = zeros(Nsamples, 2);
Zsaved = zeros(Nsamples, 1);
for k=1:Nsamples
% 위치와 속도 추정
z = GetPos();
[pos, vel] = DvKalman(z);
Xsaved(k, :) = [pos vel];
Zsaved(k) = z;
end
figure
hold on
plot(t, Zsaved(:), 'r.')
plot(t, Xsaved(:,1))
figure
plot(t, Xsaved(:,2))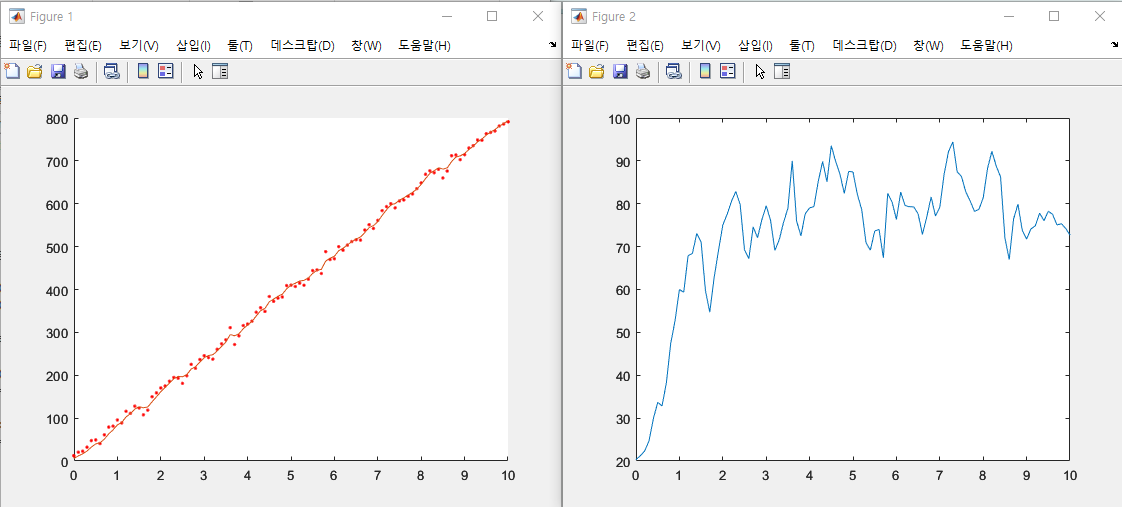
Figure 1
- 실선: 칼만 필터의 추정위치
- 점: 위치 측정값
➡ 측정잡음을 효과적으로 제거하여 추정 위치의 궤적이 더 매끄러워졌고, 열차의 이동 경향도 잘 나타나 있음
Figure 2
: 칼만 필터가 추정한 속도를 보여주는 그래프
➡ 칼만 필터 알고리즘을 사용해, 위치 정보만 가지고 속도를 제대로 추정함!
4. 속도로 위치 추정하기
이번엔 반대로 속도를 측정해서 위치를 추정해보자!
우선 측정값이 위치➡속도로 변했으니 시스템 모델에서 H가 달라져야 한다.

IntKalman(z)
- 매개변수: z (속도 측정값)
- 반환값: 위치 추정값, 속도 추정값
IntKalman.m (DvKalman.m에서 H 초기화하는 부분만 변경)
function [pos, vel] = IntKalman(z)
%
%
persistent A H Q R
persistent x P
persistent firstRun
if isempty(firstRun)
firstRun = 1;
dt = 0.1;
A = [1 dt;
0 1 ];
H = [0 1];
Q = [1 0;
0 3];
R = 10;
x = [0 20]';
P = 5*eye(2); % eye(): identity matrix
end
xp = A*x;
Pp = A*P*A' + Q;
K = Pp*H' * inv(H*Pp*H' + R);
x = xp + K*(z - H*xp);
P = Pp - K*H*Pp
pos = x(1);
vel = x(2);
endGetVel.m
function z = GetVel()
%
%
persistent Velp Posp
if isempty(Posp)
Posp = 0;
Velp = 80;
end
dt = 0.1;
v = 0 + 10*randn;
Posp = Posp + Velp*dt; % true position
Velp = 80 + v; % true speed
z = Velp;
endTestIntKalman.m
clear all
dt = 0.1;
t = 0:dt:10;
Nsamples = length(t);
Xsaved = zeros(Nsamples, 2);
Zsaved = zeros(Nsamples, 1);
for k=1:Nsamples
% 위치와 속도 추정
z = GetVel();
[pos, vel] = IntKalman(z);
Xsaved(k, :) = [pos vel];
Zsaved(k) = z;
end
figure
plot(t, Xsaved(:,1))
figure
hold on
plot(t, Zsaved(:), 'r.')
plot(t, Xsaved(:,2))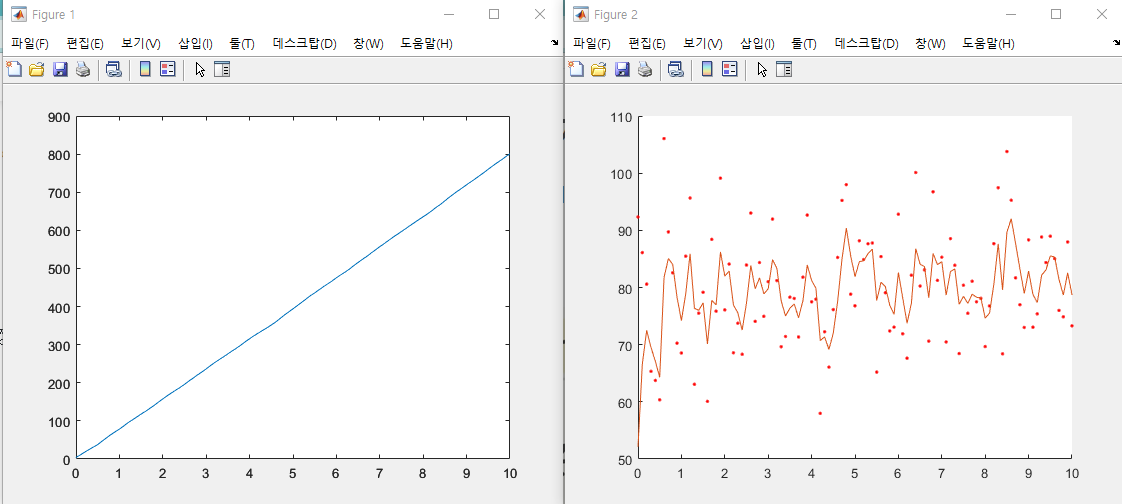
Figure 1
: 추정 위치를 그린 그래프
평균 속도가 80m/s이므로 10초에 800m 이동하는 게 정상 ➡ 추정 잘함!
Figure 2
: 측정 속도와 추정 속도 비교
- 실선: 추정 속도
- 점선: 속도 측정값
➡ 측정 잡음이 많이 제거되었고, 기준 속도인 80m/s 근처에 추정 속도가 모여 있음
5. 초음파 거리계로 속도 추정하기
앞의 예제에서는 속도가 일정했다.
이번엔 속도가 일정하지 않은 경우에도 위치로 속도를 추정해낼 수 있는지 확인해보자!
Ch3에서 다뤘던 초음파 거리계 예제를 사용해보자. 이 예제에서는 시간당 이동 거리의 변화, 즉 속도가 일정하지 않다.
TestDvKalman.m에서 GetSonar 함수로 거리를 측정해서 칼만 필터에 입력하는 걸로 바꾸면 된다.
TestDvKalman2.m
clear all
Nsamples = 500;
Xsaved = zeros(Nsamples, 2);
Zsaved = zeros(Nsamples, 1);
for k=1:Nsamples
z = GetSonar();
[pos, vel] = DvKalman(z);
Xsaved(k, :) = [pos vel];
Zsaved(k) = z;
end
dt = 0.02;
t = 0:dt:Nsamples*dt-dt;
figure
hold on
plot(t, Zsaved(:), 'r.')
plot(t, Xsaved(:,1))
figure
plot(t, Xsaved(:,2))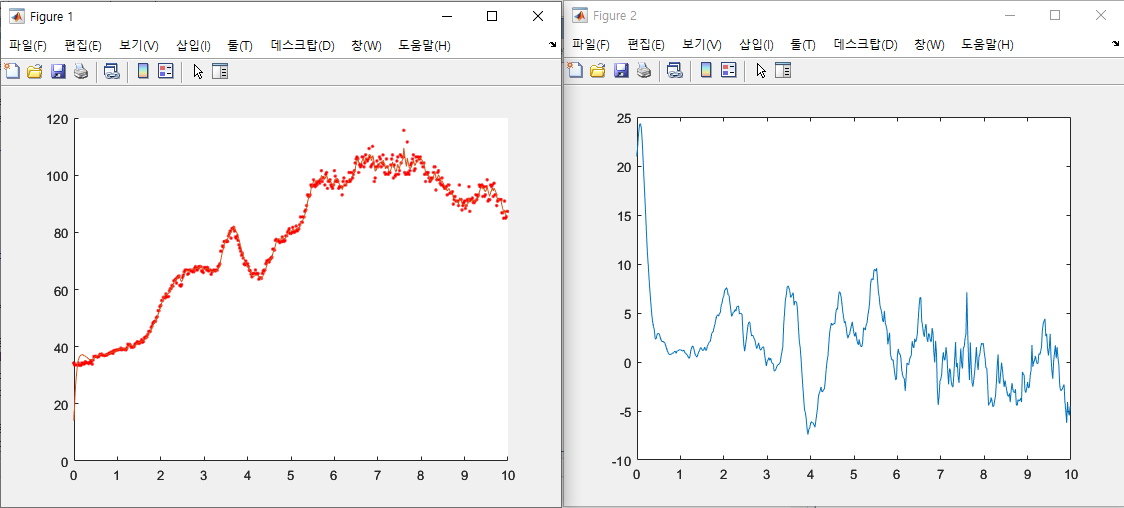
Figure 1
: 거리의 궤적을 비교한 그래프
- 실선: 칼만 필터의 추정값
- 점: 측정 거리
➡ 측정 잡음이 많이 제거되었고, 거리의 변화 추이도 잘 드러나 있다.
➡ 잡음 제거와 변화 민감성 두 가지 목표를 동시에 달성!
Figure 2
: 칼만 필터가 추정한 속도
➡ Figure 1의 추정 거리의 변화율과 Figure 2의 추정 속도를 비교해보면, 거리의 변화가 별로 없는 구간에서는 속도가 0에 가깝고, 변화가 심한 구간에서는 속도값이 크게 나타난다.
➡ 거리의 변화율 α 속도이므로 타당!
6. 효율적인 칼만 필터 함수
칼만 필터 알고리즘을 보면 칼만 이득을 계산할 때 역행렬을 한 번 계산해야 한다.
➡ 역행렬은 보통 수치해석 기법으로 구하는데, 계산 시간과 안정성 측면에서 권장❌
✔ 빠르게 실행되는 실시간 시스템에 칼만 필터를 적용할 때는 최대한 계산 시간을 단축해야 한다.
➡ 이 장의 예제와 같이 시스템 모델의 행렬이 작으면 행렬 계산식을 풀어 쓰는 게 계산 시간과 오차를 줄이는 데 도움이 된다!
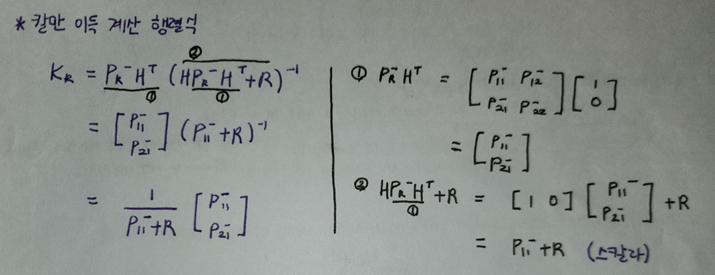
칼만 이득을 계산하는 DvKalman.m에서 칼만 이득을 계산하는 부분을 아래와 같이 변경해 DeDvKalman.m를 새로 만들자!
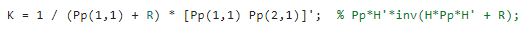
DeDvKalman 함수를 테스트해보자! 동일한 조건에서 DvKalman 함수로 추정한 결과와 비교했을 때, 두 함수의 추정 결과가 동일해야 한다.
TestDeDvKalman.m
clear all
dt = 0.1;
t = 0:dt:10;
Nsamples = length(t);
Xsaved = zeros(Nsamples, 2);
DeXsaved = zeros(Nsamples, 2);
Zsaved = zeros(Nsamples, 1);
for k=1:Nsamples
z = GetPos();
% 두 칼만 필터 함수의 추정 위치와 속도 저장
[pos, vel] = DvKalman(z);
[dpos, dvel] = DeDvKalman(z);
Xsaved(k, :) = [pos vel];
DeXsaved(k, :) = [dpos dvel];
Zsaved(k) = z;
end
figure
hold on
plot(t, Xsaved(:, 1), 'ro')
plot(t, DeXsaved(:,1))
figure
hold on
plot(t, Xsaved(:, 2), 'ro')
plot(t, DeXsaved(:,2))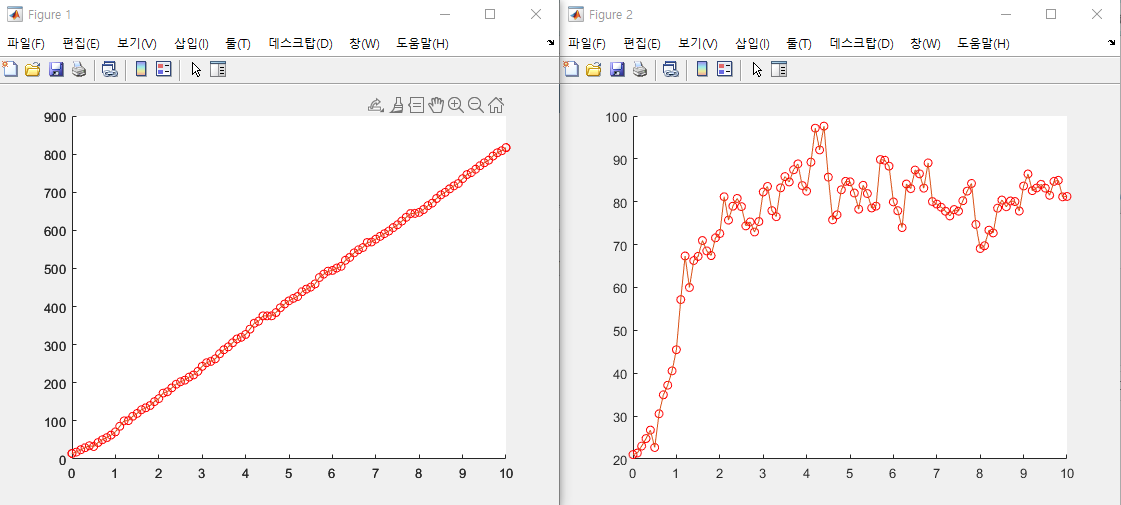
Figure 2
:속도 추정 결과 비교
- 실선: 행렬식을 풀어 쓴 결과
- 원: 행렬식으로 계산한 칼만 필터의 출력
이 절에서는 칼만 이득의 행렬식을 풀어서 계산을 간단하게 하고, 속도를 개선하는 기법을 살펴봤다.
But, 이 방법은 상태 변수가 많아서 시스템 모델의 행렬이 커지면 사용하기 어렵!
➡ 이런 경우엔 효율적인 수치해석 라이브러리 사용해야만 함
7. 시스템 모델의 힘
📌 칼만 필터는 잡음도 제거하지만, 위치 정보만 가지고 속도를 추정해내는 능력도 있다!
🤷♀️ 어떻게 측정하지도 않은 속도를 추정할까?
➡ 시스템 모델 덕분에 칼만 필터가 측정하지 않은 물리량까지 추정 가능!
저주파 통과 필터는 측정 신호에 가정❌. 새 측정값과 이전의 추정값에 가중치를 주고 더함.
➡ 측정하지 않은 물리량을 추정하는 건 불가능! 측정값이 없으면 추정도 없음!
칼만 필터는 시스템의 수학적 모델을 알고 있다고 가정!
➡ 즉 시스템이 어떤 법칙에 따라 측정값을 출력하는지 정확히 알고 있다고 전제
📌 상태 변수 사이의 연관 관계를 나타내는 시스템 모델을 통해 측정하지 않는 상태 변수를 간접적으로 추정해내는 것
❗ 하지만 시스템 모델이 실제 시스템과 많이 다르면 추정 결과도 엉망이 되고, 칼만 필터 알고리즘이 발산해서 전체 시스템이 망가질 수 있다.
