이 글은 Networkx를 활용한 네트워크 분석 기초 입문 정리 - 박건영 저 (E-book) 를 읽고 개념 정리를 한 글입니다.

정말 오랜만에 글을 작성한다. 회사 내에서 진행하고 있는 프로그램에 참여해 팀을 꾸리고 프로젝트를 진행하게 되었는데, 데이터 분석을 주제로 진행하고 있다.

프로젝트를 진행하면서 필요한 내용을 찾다보니, 네트워크 분석 쪽에 대한 학습이 필요해서 책을 구매하고 공부 중이다.

이 책은 기본적인 네트워크 분석 기법, 개념에 대해 잘 설명해주고 있으며, 해당 내용을 한번 공부해보고 싶었던 터라 이렇게 글로도 정리하게 되었다.

1장. 네트워크 과학의 개요

1.1 네트워크 과학의 정의

네트워크: 현실 세계의 각종 시스템(체계)을 노드 (Node: 개체)와 링크 (Link: 개체간 연결관계)로 표현하는 모델링 방법

네트워크 과학: 현실 세계를 네트워크 형태로 모델링한 후 구성된 네트워크의 구성정보(노드, 링크)들을 과학적으로 분석하는 방법론을 다루는 학문

1.2 네트워크 과학의 범위

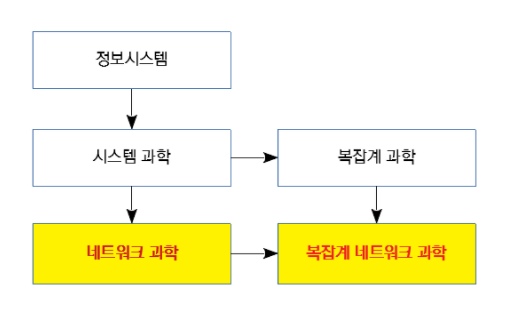
현재는 주로 복잡계 네트워크 과학이 대상이다.

네트워크 과학의 3가지 연구 범위

(1) 특정 시스템의 숨겨진 현상을 파악하는 방법론 제공

• 사회 네트워크, 복잡계 네트워크 등

(2) 기존의 과학적 접근방식으로 해결이 어려웠던 특정 현상에 대해 해석하는 방법론

• 제공 나비효과 현상, 확산 현상 등

(3) 다양한 시스템에서 발생하는 각종 문제들에 대한 해결책 제공

• 전염병 감염경로, 조직 연구 등

2장 네트워크 분석 기법의 기초 이론

2.1 행렬 (Matrix)의 기초

(1) 행렬의 정의

행렬 (Matrix): 수, 기호, 수식 등을 네모꼴로 배열하고 행과 열의 형태로 묶어 표시한 것
m: 행, 열: n, m x n: 크기 -> M (I, j)로 표현

(2) 행렬의 형태

1) 행과 열의 개수 여부
정사각 행렬 (정방행렬): m = n -> n x n 행렬
직사각 행렬: m != n

2) 행과 열의 값의 형태 여부
이진행렬 (Binary Matrix): 행과 열의 값이 이진값 (0 또는 1)을 가지는 행렬
가중치 행렬 (Weight Matrix): 행과 열의 값이 가중치를 가지는 행렬

3) 행렬의 대각선 기준에 따른 대칭 여부
대칭 행렬: 행렬 요소의 값이 행과 열 사이에 대칭 (무방향 네트워크)
비대칭 행렬: 행렬 요소의 값이 행과 열 사이에 대칭이 아닌 행렬

4) 행과 열의 개체 속성 동일 여부
일원모드 행렬 (1-mode Matrix): 행과 열 모두 개체 속성이 같은 경우의 행렬

• ex) 사람 x 사람

이원모드 행렬 (2-mode Matrix): 행과 열의 개체 속성이 서로 다른 경우의 행렬

• ex) 사람 x 사건
  보통 가로는 개체, 세로는 사건, 관계는 소속 여부 M (I, j) = 1

(3) 행렬의 연산
덧셈, 뺄셈, 곱셈

(4) 행렬의 치환
주어진 행렬의 패턴 파악 등의 특정 목적 위해 기존 행렬의 행과 열의 순서를 재배열하는 것을 의미

(5) 행렬의 분할
주어진 행렬의 각 요소들을 특정 집단으로 분할한 행렬, 블록 행렬/블록/슈퍼 노드
이를 블록모델링이라 한다.

2.2 그래프 이론의 기초

그래프 = 네트워크

(1) 그래프의 구성 요소
그래프: 점 (Vertex, Node), 선 (Edge, Link) 로 구성된 도형

그래프 G는 점 V와 선 E의 집합
G = (V, E)

다른 점들과 연결된 선이 없는 점 = 고립점

(2) 그래프 선의 방향 요소
1) 무방향 그래프
2) 방향 그래프

(3) 그래프 선의 관계 요소
1) 이진 그래프: 모든 선이 관계의 유무만 표시하는 그래프
2) 계량(가중) 그래프: 모든 선의 관계 정도가 동일하지 않아 각 관계마다 그 크기를 표시하는 그래프
3) 균형 그래프: 모든 관계가 동일한 성향을 나타내는 그래프
4) 비균형 그래프: 관계 간 서로 다른 성향을 나타내는 그래프

(4) 그래프 선의 연결성 요소
1) 완전연결 그래프: 모든 점의 쌍을 연결한 선이 존재하는 그래프

• 무방향성 완전연결 그래프의 선 개수 [n: 점의 개수] = [n * (n-1)] / 2
• 방향성 완전연결 그래프의 선 개수 [n: 점의 개수] = n * (n-1)

2) 부분연결 그래프: 전체 점의 쌍 중 일부 점의 쌍에 연결선이 존재하지 않는 그래프
3) 희소 그래프: 많은 점들 중 극히 소수의 점들만 연결 (=희소성) 된 그래프

(5) 차수
차수 (Degree): 임의의 점과 그 이웃하는 점들 사이에 연결된 선의 수
1) 내차수: 임의의 한 점으로 들어오는 선의 개수
2) 외차수: 임의의 한 점에서 나가는 선의 개수

(6) 경로
경로: 그래프 내 임의의 두 점이 연결되어 있을 때, 반복되지 않은 선들의 연결 순서
1) 경로의 길이: 경로 내의 전체 선의 개수

• 임의의 2개 점 사이 길이가 L일 때, 경로 상 점의 개수: L+1
• 임의의 2개 점 길이가 1일 때, 2개 점은 “인접조건” 이라 함. (이웃관계)

2) 단순 경로: 그래프 내의 모든 점들을 지나는 경로 (이 경우, 모든 점들이 연결되어 있어야함)

(7) 거리: 임의의 2개 점 사이에 존재하는 경로 중 가장 짧은 경로 (최단거리)

(8) 직경: 직경은 한 그래프 내의 거리 중 가장 길이가 긴 거리

(9) 사이클: 그래프 경로에서 시작점과 끝점이 연결되는 경로, 최소 3개 이
상의 점들 사이에 닫힌 형태의 경로

(10) 인접성: 임의의 2개 점이 하나의 선으로 연결되어 있는 경우

(11) 연결성: 그래프 내의 모든 점들 간에 경로가 존재하는 경우
연결성 존재하는 경우 연결된 그래프, 아니면 분리된 그래프

(12) 컴포넌트: 한 그래프 내에서 연결된 부분 그래프를 의미
한 그래프의 서브 그래프 들 중 점들 사이가 연결된 서브 그래프만을 컴포넌트

(13) 코어: 모든 점들이 연결되어 있어 고립점이 하나도 없는 서브그래프, 모든 점들이 최소한 n차수 만큼 연결된 서브그래프 = n-코어 서브그래프

(14) 파당 (Clique): 3개 이상의 점을 포함한 가장 큰 완전연결 그래프 형태의 서브그래프, 2개 이하의 점을 포함한 완전연결 그래프는 파당에 해당되지 않는다. 파당의 크기는 포함된 점의 개수를 나태낸다.

(15) 표현방식

1) 행렬을 이용한 방식

A. 인접행렬 (Adjacency Matrix)
각 점들 간에 존재하는 인접연결 관계를 표시한 행렬, 그래프의 점의 개수가 n이면, 인접행렬은 n차 정방행렬로 표현됨.

• 인접행렬로 표현가능한 선의 최대수: n(n-1)

B. 노드리스트
인접행렬 내 인접한 선이 있는 점들만 표시하는 방법
존재하는 선의 개수가 아주 적을 때 표현공간 크기를 크게 줄일 수 있는 장점이 있지만, 선의 강도를 표시할 수 없는 단점이 있다.

C. 에지리스트
인접행렬 내 점이 연결된 선들의 전체 리스트를 표시하는 방법

2) 시각화: 각 점들 간에 존재하는 인접연결 관계를 점과 선만으로 표현된 형태

2.3 네트워크 이론의 기초

(1) 그래프 이론과 네트워크 이론의 주요 용어 비교

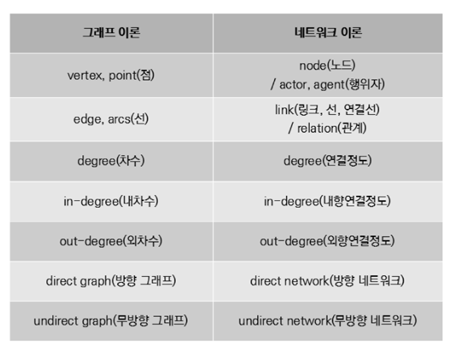
(2) 네트워크 구성 요소
노드: 상호 고유한 속성을 가지는 행위자
링크: 노드들 간의 연결 관계

(3) 네트워크의 제어 규칙
미시적 규칙 (Micro-rules = 국지적 (Local) 규칙): 네트워크 내에서 노드 및 링크의 형성과 관련된 규칙 (노드의 연결형태를 설명하는 규칙)
거시적 규칙 (Macro-rules = 전역적 (Global) 규칙): 네트워크의 전역적 특성 발현과 관련된 규칙 (전체 네트워크의 특성 및 그로 인한 발현된 현상을 설명하는 규칙

(4) 네트워크의 표현 방식
1) 시각적 형태: 그래프
2) 데이터 처리 형태: 행렬 – 네트워크/그래프의 연결관계 수치화

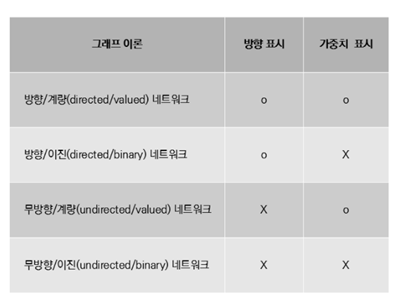
(5) 네트워크의 유형

관심 기준에 따라 구분

- 링크 방향 및 가중치 여부

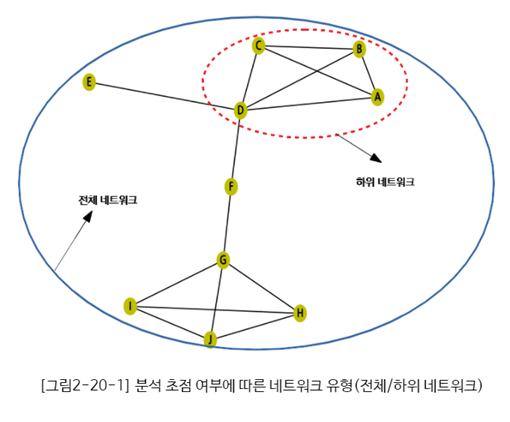
- 분석 초점 여부

1) 전체 네트워크: 모델링하고자 하는 전체 행위자로 구성된 네트워크 (완전 네트워크, 전역 네트워크 등이 해당)

2) 하위 네트워크: 전체 네트워크에서 별도로 구분하여 구성된 하위 집단 네트워크 (특정 컴포넌트, 파당, 클러스터 등이 해당)

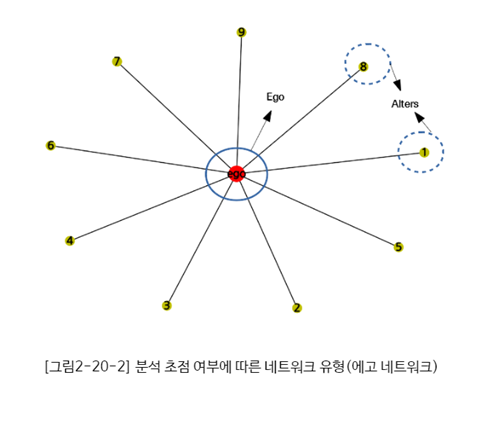
3) 에고 네트워크: 한 개인의 에고 (Ego)를 중심으로 해서 그 개인과 다른 노드 간 연결을 표현한 네트워크 (국지 네트워크 (Local Network), 에고 중심 네트워크 (Ego-Centric Network) 등이 해당)

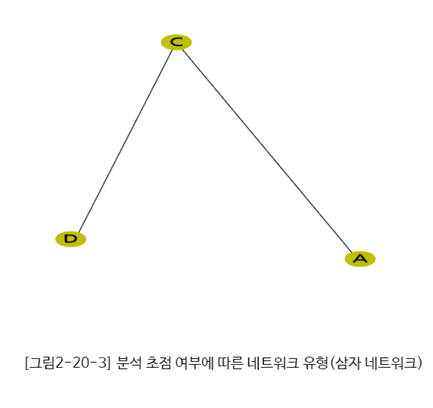
4) 삼자 네트워크 (Triad Network): 3개 노드 간의 관계를 토대로 분석하는 네트워크 (에고 네트워크의 중개성 분석 등이 해당)

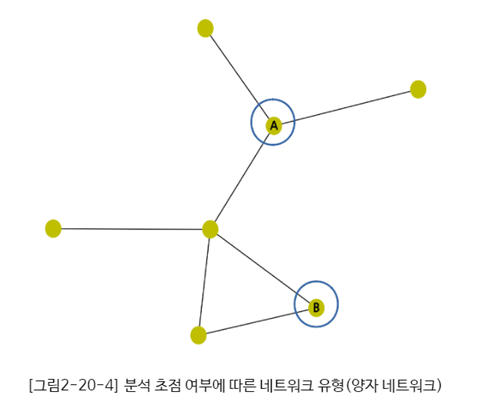
5) 양자 네트워크 (Dyad Network): 2개 노드 간의 관계를 토대로 분석하는 네트워크 (네트워크의 연결거리, 거리경로 분석 등이 해당)

- 네트워크 변화 여부

1) 정적 네트워크 (Static Network): 시공간의 변화 여부와 상관없이 네트워크의 노드와 링크가 고정된 네트워크 (구조적인 형태의 분석을 중요시하는 경우에 사용되는 네트워크

2) 동적 네트워크 (Dynamic Network): 시공간의 변화에 따라 네트워크의 노드와 링크가 변화되는 네트워크 (시공간 변화에 따른 동적 변화 특성 분석을 중요시하는 경우 사용되는 네트워크)

- 네트워크 규모 여부
1) 소규모 네트워크 (Small Network): 노드 수가 100개 미만인 네트워크

2) 중규모 네트워크 (Medium Network): 노드 수가 100개 ~ 1000개 사이인 네트워크

3) 대규모 네트워크 (Large Network): 노드 수가 1000개 이상인 네트워크

- 노드 연결 형태 여부
1) 정규적 연결: 모든 노드의 연결 형태가 동일한 형태로 된 네트워크 (정규형 격자 네트워크)

2) 무작위 연결: 노드의 연결 형태가 임의적인 형태로 연결된 네트워크 (무작위 네트워크)

3) 선호적 연결: 노드의 연결 형태가 특정 선호 형태를 따르는 네트워크 (무척도 네트워크)

- 현실 세계 존재 가능성 여부
1) 이상형 네트워크: 현실 세계의 존재 가능성이 낮은 유형의 네트워크 (무작위형, 전방위형 네트워크 해당)

• 무작위형 네트워크: 노드 간의 군집화 계수는 낮지만, 노드들의 경로거리가 짧은 네트워크 (혼란 또는 무질서 현상 표현)
• 전방위형 네트워크: 노드 간의 군집화 계수는 높고 노드들의 경로거리가 긴 네트워크 (질서가 있는 현상 표현)

2) 허브형 네트워크: 현실 세계에 실제 존재할 수 있는 유형의 네트워크 (단허브형, 다허브형, 탈허브형 네트워크 해당)

• 단허브형 네트워크: 단일 허브 노드에 노드들이 결집되는 현상이 나타나는 네트워크 (중앙집중적 형태)
• 다허브형 네트워크: 다수의 허브 노드들을 중심으로 노드들이 국지적인 결집 현상이 나타나는 네트워크
• 탈허브형 네트워크: 특정한 허브 노드를 경유하지 않고 노드들 간의 교류가 만들어지는 네트워크 (Peer-to-Peer 형태)

(6) 네트워크의 주요특성

1) 역동성 (Dynamics): 네트워크의 미시적 특징 중 하나, 네트워크가 끊임없이 진화하고 자기조직화가 되도록 구조가 변화하는 것 (동적 네트워크의 특성)

2) 군집성 (Clustering): 네트워크의 미시적 특징 중 하나, 네트워크의 유유상종 현상 (전역적으로는 느슨한 연결, 국지적으로는 강한 응집력 나타내는 특성)

3) 중심성 (Centrality): 네트워크의 미시적 특징 중 하나, 네트워크 내에서 특정 노드가 가지는 중심 역할의 영향력 (노드 단위에서 나타나는 특성)

• 중심성은 각 노드 간 중심역할 크기의 순위화를 통해 핵심적인 노드들을 확인할 수 있기에 네트워크 분석시 매우 중요한 개념

4) 복잡성 (Complexity): 네트워크의 거시적 특징 중 하나, 복잡계 네트워크에 대해 구조적 속성 (역동성, 군집화, 중심성)만으로 설명할 수 없는 복잡계만이 가지는 특성을 의미

• 현재 네트워크 과학 분야에서 가장 많은 연구

5) 창발성 (Emergence): 네트워크의 거시적 특징 중 하나, 네트워크가 성장하면서 발생하는 수많은 국지적 변화로 인해 나타나는 거시적 수준의 변화, 전체가 부분의 합보다 큰 시너지 효과를 나타내는 현상을 의미 (단순계와 복잡계 네트워크를 구분하는 중요한 기준)

(7) 네트워크 효과

네트워크의 구조적 형태에서 발생하는 효과, 네트워크 내 구조적 위치에 따라 해당 노드가 얻을 수 있는 이득이나 주변에 미치는 영향력 여부도 이에 포함

1) 네트워크의 외연적 효과: 전체 네트워크에서 특정 노드가 차지하는 위치에 의해 발생하는 지위나 영향이 해당 노드와 연결된 다른 노드들에게 미치는 효과

2) 네트워크의 시너지 효과: 네트워크를 통해 노드들 간에 자원 교환이 이루어짐에 따라 발생하는 협력 또는 상승 효과

• 노드의 거래 비용과 불확실성은 낮추고 기술이나 지식 교류를 통한 혁신이나 성장은 높임

3) 네트워크의 형태 효과: 네트워크의 구조적 형태 (구조적 공백 등) 에서 발생하는 효과

• 메트칼프 법 (Metcalfe’s Law): 노드 수가 n일 때, 네트워크의 구성원이 특정 수준에 이를 때까지 네트워크 효과는 n의 제곱에 비례한다는 법칙

• 리드 법칙 (Reed’s Law): 노드 수가 n일 때, 네트워크의 가치는 2의 n제곱에 비례한다는 법칙

2.4 네트워크 분석의 개요

연구대상 또는 현상을 네트워크 형태로 표현하고 분석하는 작업,
주로 노드의 개별적 속성에 대한 분석이 아닌 ‘노드와 노드 간 관계의 속성’에 초점

(1) 네트워크 분석 방법론

1) 연결 (Connectivity) 방법론: 네트워크 안의 노드들 간의 근접성 (Closeness)에 기초하여 네트워크 내 군집들을 발견하는 것이 목적인 방법론, 네트워크 구조 해석에 중점을 둔다.

2) 위치 (Position) 방법론: 네트워크 안의 노드들 간의 위치 또는 역할의 유사성 (Similarity)에 기초하여 네트워크 내 군집들을 발견하는 것이 목적인 방법론, 네트워크 구조 해석에 중점

3) 구조 방법론: 네트워크의 구조 자체가 그 안의 노드들에게 미치는 영향성을 발견하는 것이 목적인 방법론, 네트워크 구조 자체의 해석보다는 네트워크 구조가 네트워크 내 구성원들에 대한 제약요소로서 미치는 영향을 해석

(2) 네트워크 분석 단계

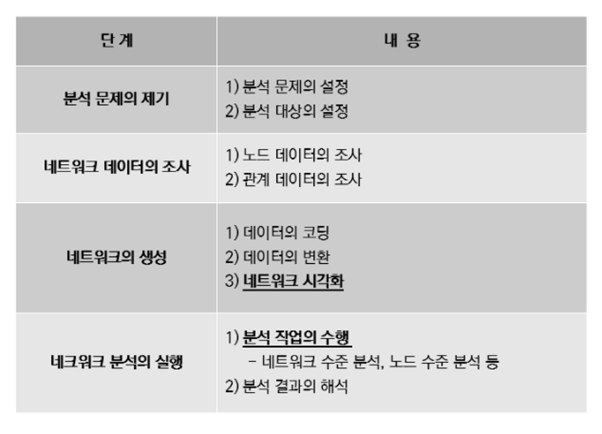
3장 네트워크 분석 도구

3.1 NetworkX의 주요 특징

(1) 표준 그래프이론과 통계 물리학 기능 탑재
(2) 다양한 전형적 형태의 그래프 및 합성 네트워크 구현 지원
(3) Node는 파이썬 객체로서 다양한 형태 (Text, 이미지, 시계열 데이터 등)로 변이 용이
(4) Edge는 임의 형태의 데이터 포함 가능
(5) OpenSource 형태
(6) 파이썬 기반 여러 OS 가능

3.2 NetworkX의 설치

기존에 Anaconda 가 깔려있어서 conda 가상환경에서 실행했다.
Python 3.6 환경에서 진행했으며, Jupyter Notebook 으로 코드를 작성했다.

conda activate py36
conda install -c anaconda networkx

3.3 NetworkX 기본 사용법

(1) 기본 명령어

1) Graph(): 그래프 구조 생성

• Graph(): 무방향성 그래프 구조
• DiGraph(): 방향성 그래프 구조
• G.to undirected(): 생성된 G 그래프 구조를 무방향성으로 변환 (G -> 생성된 그래프)
• G.to directed(): 생성된 G 그래프 구조를 방향성으로 변환

모든 자료의 출처: Networkx를 활용한 네트워크 분석 기초 입문 정리 - 박건영 저 입니다.